1.5.K
Video
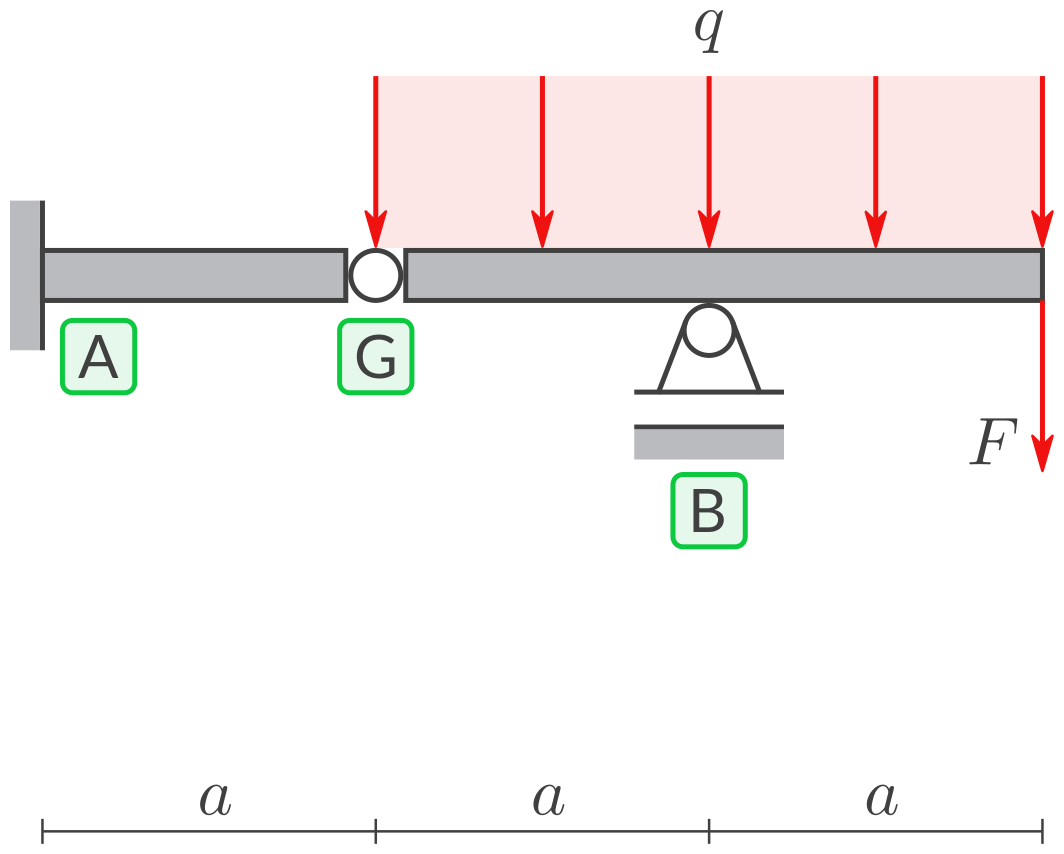
Gegebene Symbole: \(a, F, q.\)
Berechnen Sie die Lagerreaktionen bei A und B und die Kräfte im Gelenk G. Gehen Sie wie folgt vor.
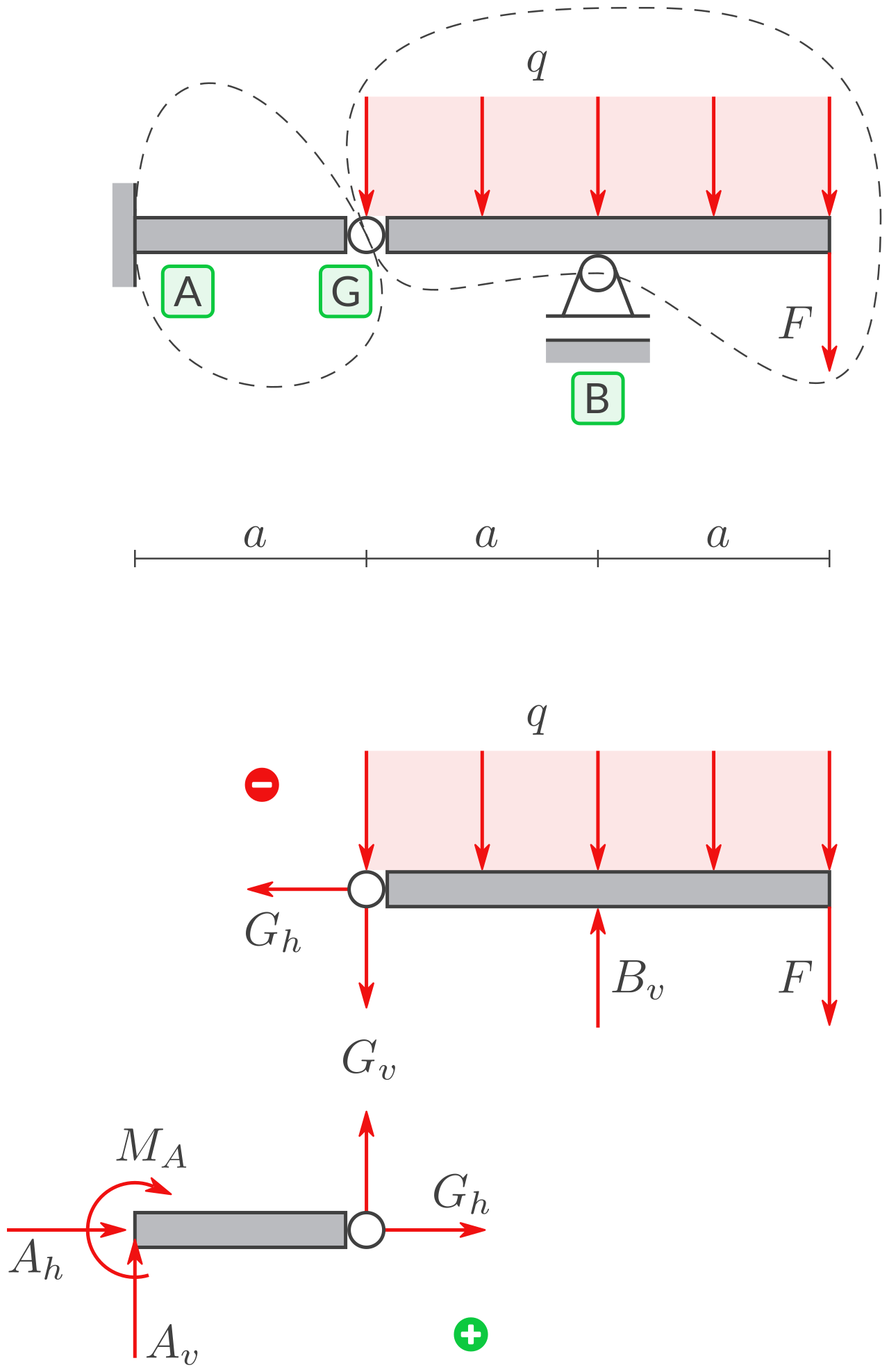
a) Freischneiden
Schneiden Sie:
bei G durch das Gelenk, an der Grenze zwischen linkem und rechtem Balken
bei A, an der Grenze zwischen linkem Balken und Lager bei A
bei B, an der Grenze zwischen rechtem Balken und Lager bei B
Zeichnen Sie zwei Freikörperbilder: Eins für den Balken links - und eins für den Balken rechts.
b) Resultierende und Gleichgewichtsbedingungen
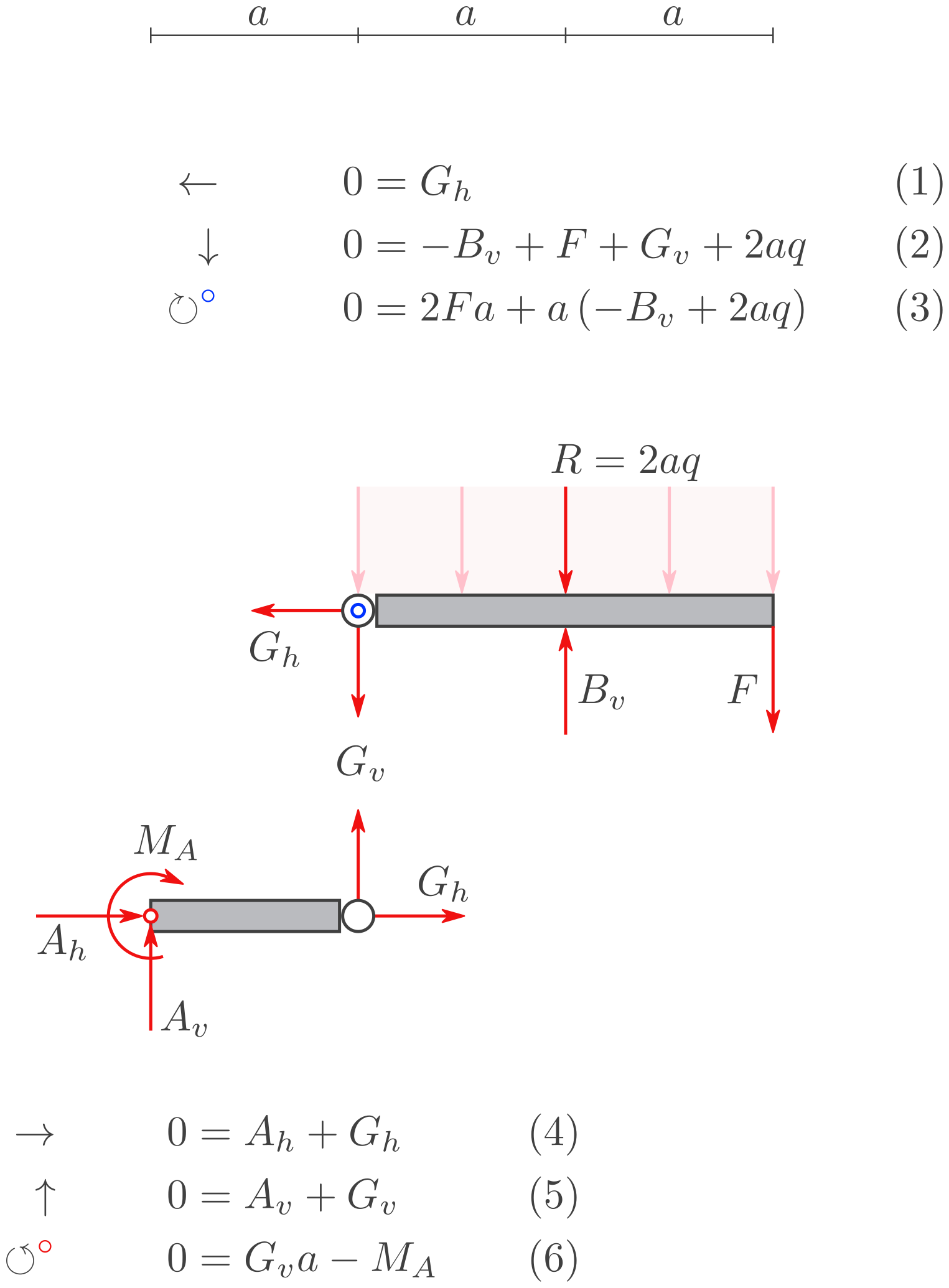
Berechnen Sie die Resultierende der verteilten Kraft. Und geben Sie für beide Körper drei Gleichgewichtsbedingungen an. Nummerieren Sie die Gleichungen, und zählen Sie die Unbekannten. Zeigen Sie, dass Sie 6 Gleichungen für 6 Unbekannte haben.
c) Lösen des Gleichungssystems
Lösen Sie das Lineare Gleichungssystem bestehend aus 6 Gleichungen für 6 Unbekannte. Berechnen Sie die 6 Unbekannten für die gegebenen Symbole.
Lösung für die 6 Unbekannten \(A_h, A_v, M_A, B_v, G_h, G_v\):Lösung
d) Lösung für gegebene Größen
Berechnen Sie alle Lagerreaktionen und die Gelenkkräfte für die Größen:
Lösung
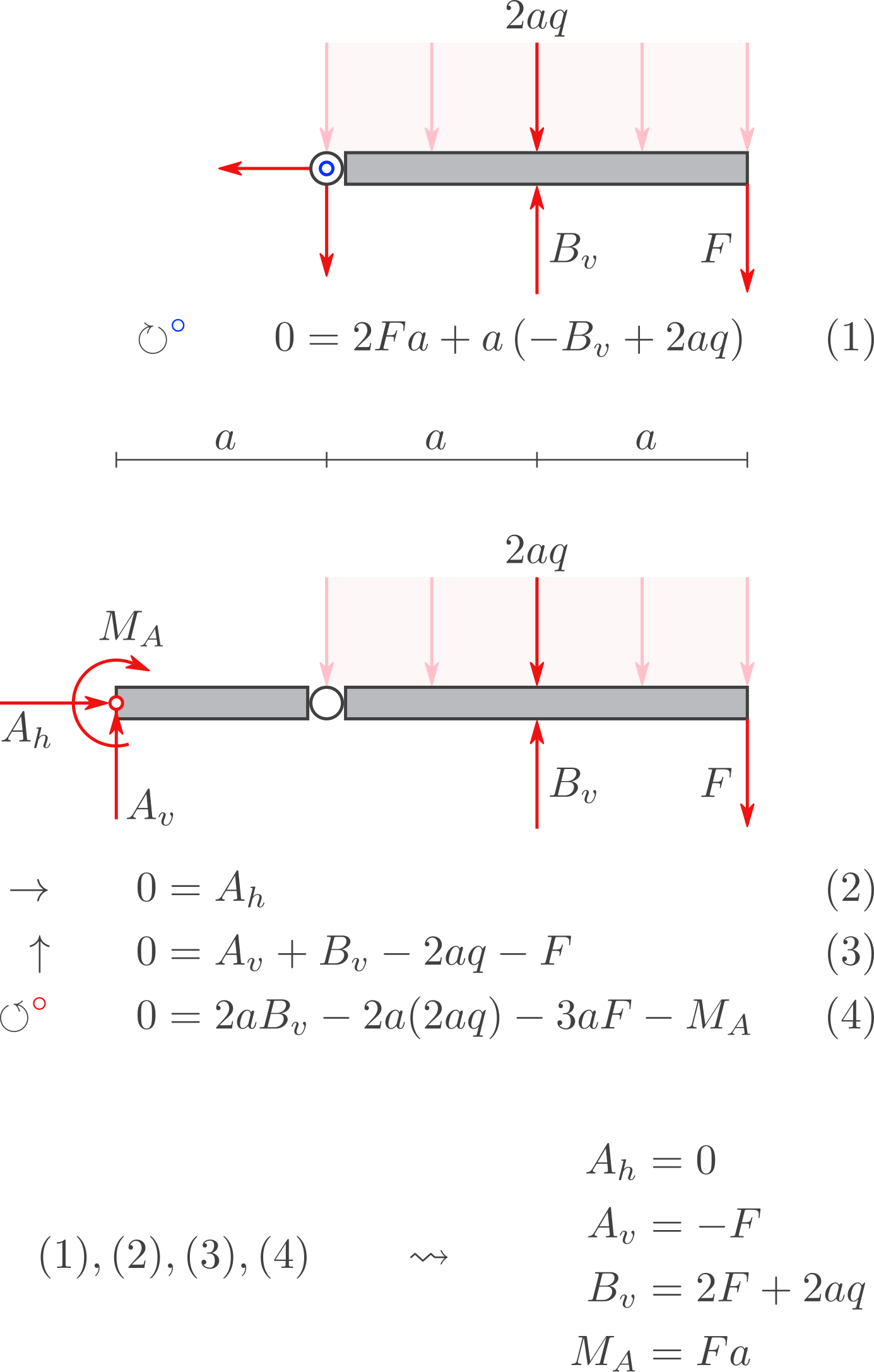
e) Nur Lagerreaktionen
Zeigen Sie eine Möglichkeit, mit geeigneten Freischnitten und Gleichgewichtsbedingungen die Lagerreaktionen zu berechnen, ohne die Gelenkkräfte berechnen zu müssen.
Nachfolgend ein Programm, dass Sie ausführen können: Auf dem PC z.B. mit Anaconda. Im Browser (online) in drei Schritten: Copy: Source Code in die Zwischenablage kopieren. Paste: Source Code als Python-Notebook einfügen z.B. auf: JupyterLite oder JupyterLab oder Play: Ausführen. Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.SymPy
from sympy import *
from sympy.physics.units import kg, m, s, newton
def print_each(sol):
for x in sorted(sol,key=default_sort_key):
tmp = x
tmp = str(tmp)+":"
pprint(tmp)
tmp = sol[x]
tmp = tmp.subs(sub_list)
if x != MA:
tmp /= newton
tmp = str(tmp)+" N"
else:
tmp /= newton*m
tmp = str(tmp)+" Nm"
pprint(tmp)
pprint("\n")
a, F, q = var("a, F, q")
sub_list=[
( a, 1 *m ),
( F, 1 *newton ),
( q, 1 *newton/m ),
]
pprint("Solution 1:")
# 6 Unknowns:
Ah,Av,MA,Bv,Gh,Gv = var("Ah,Av,MA,Bv,Gh,Gv")
unks = [Ah, Av, MA, Bv, Gh, Gv]
# 6 Equations / Equilibrium Conditions:
R = 2*a*q
eq1 = Eq( Gh, 0 )
eq2 = Eq( - Bv + F + Gv + R, 0 )
eq3 = Eq( 2*a*F + a*(-Bv + R), 0 )
eq4 = Eq( Ah + Gh, 0 )
eq5 = Eq( Av + Gv , 0 )
eq6 = Eq( Gv*a - MA, 0 )
eqs = [eq1, eq2, eq3, eq4, eq5, eq6]
sol = solve(eqs, unks)
pprint(sol)
print_each(sol)
pprint("\nSolution 2:")
# 4 Unknowns:
Ah, Av, MA, Bv= var("Ah, Av, MA, Bv")
unks = [Ah, Av, MA, Bv]
# 4 Equations:
eq1 = Eq( 2*F*a + a*(-Bv + R), 0 )
eq2 = Eq( Ah, 0 )
eq3 = Eq( Av + Bv - R - F, 0 )
eq4 = Eq( 2*a*Bv -2*a*R -3*a*F - MA, 0 )
eqs = [eq1, eq2, eq3, eq4]
sol = solve(eqs, unks)
pprint(sol)
print_each(sol)
Solution 1:
{Ah: 0, Av: -F, Bv: 2⋅F + 2⋅a⋅q, Gh: 0, Gv: F, MA: F⋅a}
Ah:
0 N
Av:
-1 N
Bv:
4 N
Gh:
0 N
Gv:
1 N
MA:
1 Nm
Solution 2:
{Ah: 0, Av: -F, Bv: 2⋅F + 2⋅a⋅q, MA: F⋅a}
Ah:
0 N
Av:
-1 N
Bv:
4 N
MA:
1 Nm