2.4.2.J

FEM-Lösung

siehe B2.A

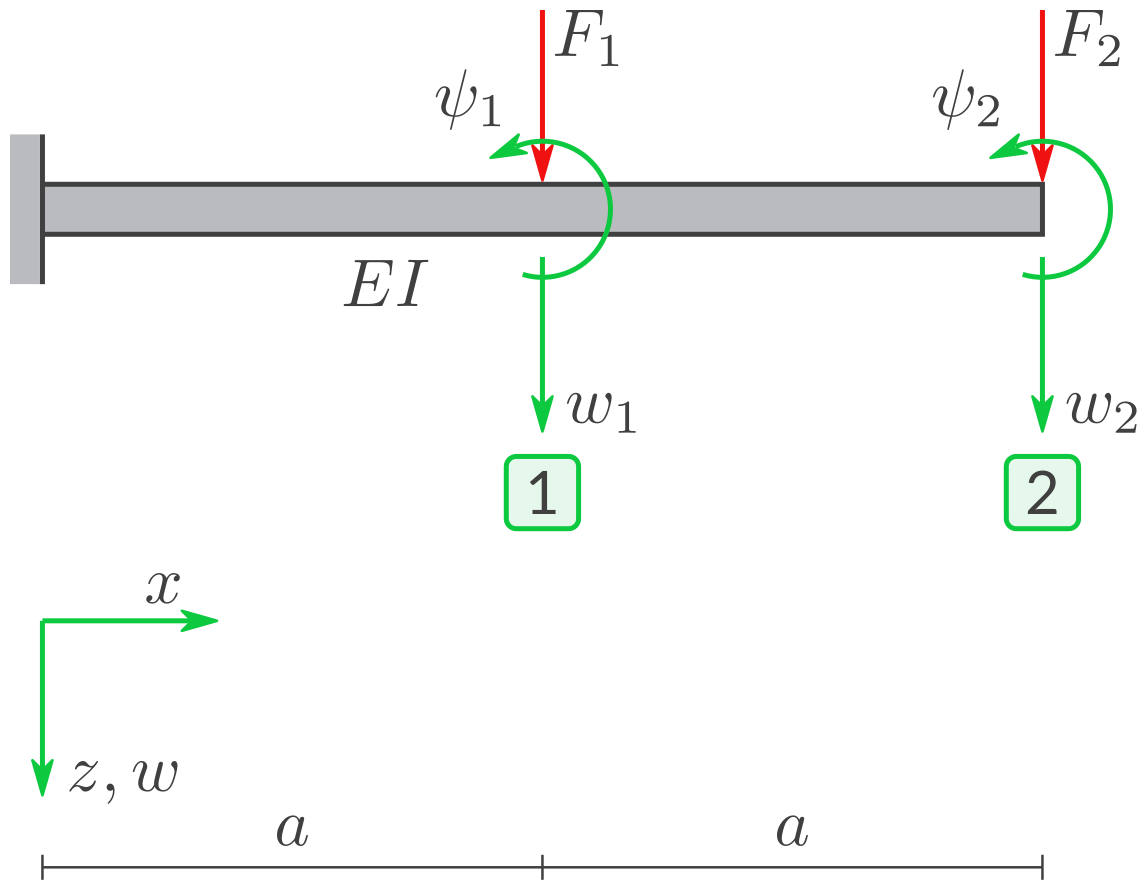
../../../../_images/2.4.2.J_1.png

Gegebene Symbole: \(a, EI, F_1, F_2.\)

Ein Kragbalken ist belastet durch zwei Kräfte \(F_1\) und \(F_2\) und erleidet Verformungen \(w_1, \psi_1, w_2, \psi_2.\)

Berechnen Sie die Querverschiebungen \(w_1\) und \(w_2\) sowie die Neigungswinkel \(\psi_1\) und \(\psi_2\). Beachten Sie, dass die Deformation aufgrund \(F_1\) und \(F_2\) die Superposition ist aus der Deformation aufgrund \(F_1\) und der aufgrund \(F_2.\)

Formeln aus Literatur

Gegeben sind außerdem folgende Informationen für einen allgemeinen Kragbalken unter einer variabel positionierten Last \(\boldsymbol F\).

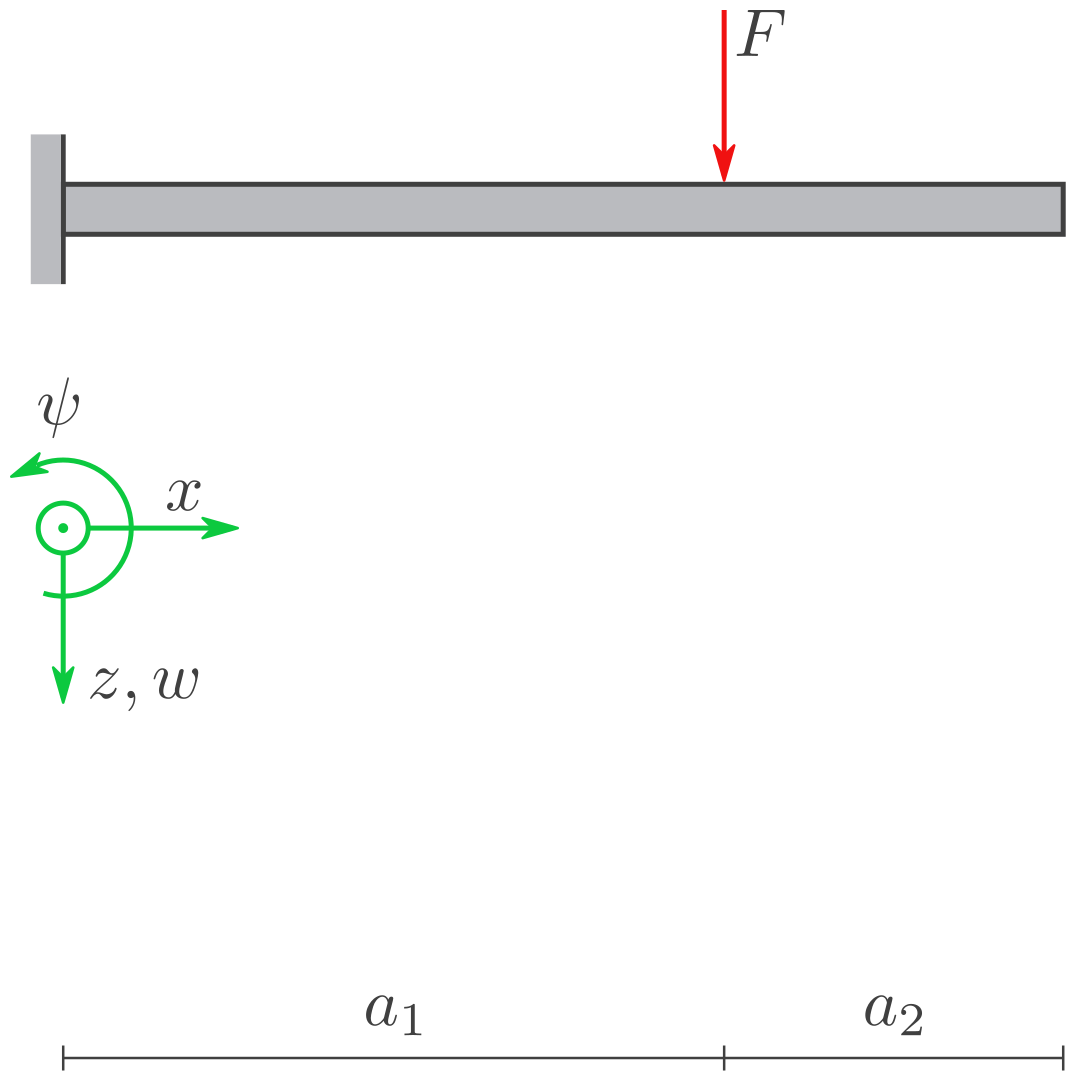
../../../../_images/2.4.2.J.png

Sei wie im Bild dargestellt:

  • \(a_1\): Der Abstand zwischen der Einspannung und \(\boldsymbol F\).

  • \(a_2\): Der Abstand zwischen \(\boldsymbol F\) und dem Ende des Balkens.

Hiermit gilt Folgendes: Wirkt an der Position \(a_1\) eine Kraft \(F\) und setzt sich der Balken dahinter fort um \(a_2\). Dann gilt für die Verschiebung \(w\) und den Neigungswinkel \(\psi\) an einer Position \(\xi\):

\begin{align} \label{eq-2.4.2.J-1} w = \tfrac{F (a_1+a_2)^3}{6EI} \left( 3 \xi^2 r - \xi^3 + \langle \xi - r \rangle^3 \right)\tag{1} \end{align}
\begin{align} \label{eq-2.4.2.J-2} \psi = -\tfrac{F (a_1+a_2)^2}{6EI} \left( 6 \xi r - 3\xi^2 + 3 \langle \xi - r \rangle^2 \right) \tag{2} \end{align}

mit \(\left(r, \xi\right)\) und der Föppl-Klammer für \(n\ge 0\) gemäß:

\begin{align*} \left( r, \xi \right) &= \left(\tfrac{a_1}{a_1+a_2} , \tfrac{x}{a_1+a_2} \right) & \\ \langle \xi-r \rangle^n &= \begin{cases} 0 & \xi < r \\ (\xi-r)^n & \xi \ge r \end{cases} \end{align*}

Herleitung von (2) aus (1)

(1) abgeleitet nach \(\xi\):

\[EI \tfrac{\partial w}{\partial \xi} = \tfrac16 F (a_1+a_2)^3 \left\{ 6 \xi r - 3\xi^2 + 3 \langle \xi - r \rangle^2 \right\}\]

Weiterhin ist \(\tfrac{\partial \xi}{\partial x} = \tfrac{1}{a_1+a_2}\), so dass:

\[\begin{split}EI w' &= EI \tfrac{\partial w}{\partial \xi}\tfrac{\partial \xi}{\partial x} \\ &= \tfrac16 F (a_1+a_2)^3 \left\{ 6 \xi r - 3\xi^2 + 3 \langle \xi - r \rangle^2 \right\} \tfrac{1}{a_1+a_2} \\ &= \tfrac16 F (a_1+a_2)^2 \left\{ 6 \xi r - 3\xi^2 + 3 \langle \xi - r \rangle^2 \right\} \\ EI \psi = - EI w' &= - \tfrac16 F (a_1+a_2)^2 \left\{ 6 \xi r - 3\xi^2 + 3 \langle \xi - r \rangle^2 \right\}\end{split}\]

Untersuchen Sie die Struktur. Gehen Sie wie folgt vor.

a) Berechnen der Deformationen

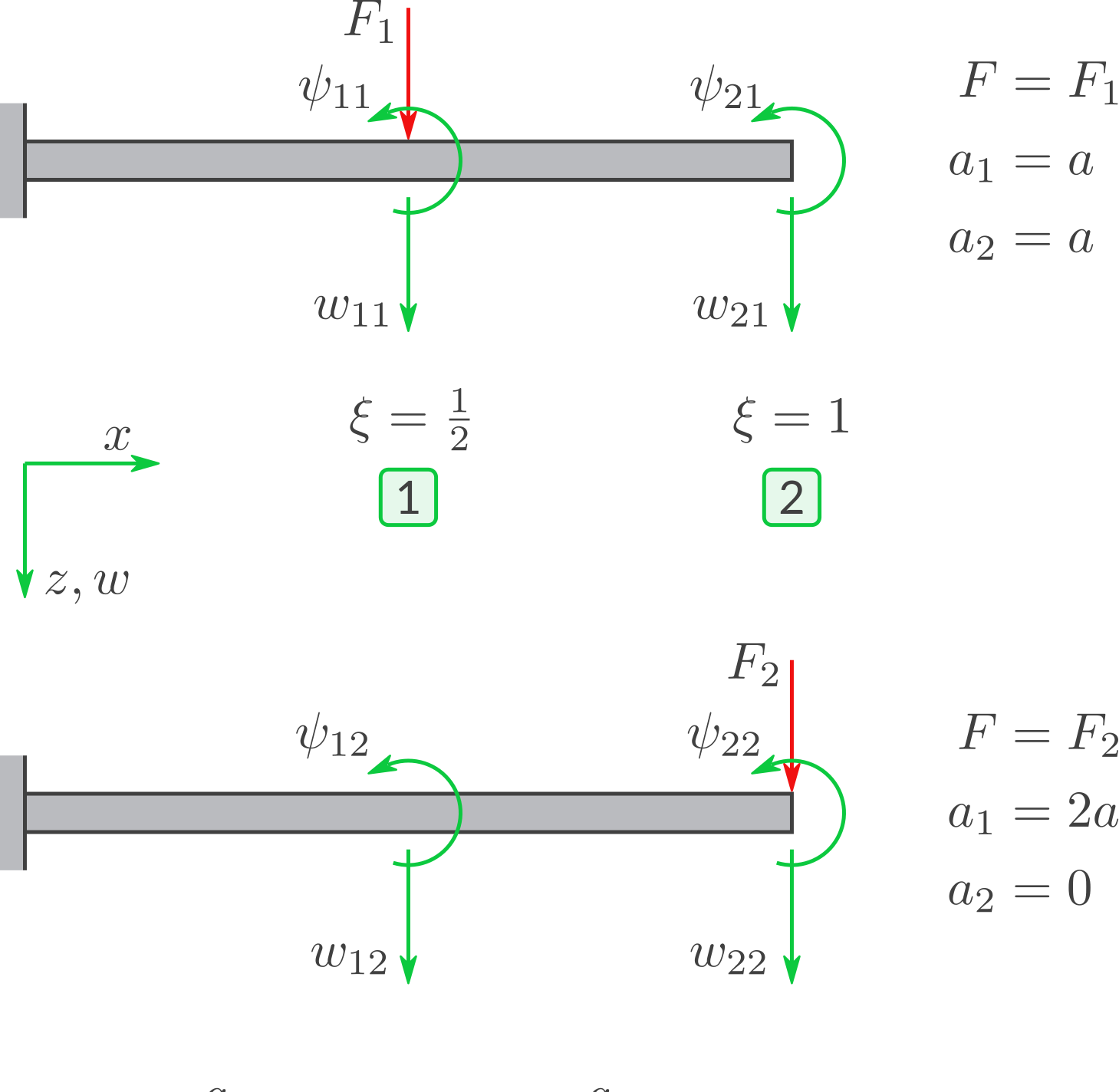
../../../../_images/2.4.2.J_2.png

Werten Sie (1) und (2) aus. Zeigen Sie, dass:

\[\begin{split}\left( w_{11}, \psi_{11} \right) &= \left( \tfrac{F_{1} a^{3}}{3 EI}, - \tfrac{F_{1} a^{2}}{2 EI} \right) \\ \left( w_{12}, \psi_{12} \right) &= \left( \tfrac{5 F_{2} a^{3}}{6 EI}, - \tfrac{3 F_{2} a^{2}}{2 EI} \right) \\ \left( w_{21}, \psi_{21} \right) &= \left( \tfrac{5 F_{1} a^{3}}{6 EI}, - \tfrac{F_{1} a^{2}}{2 EI} \right) \\ \left( w_{22}, \psi_{22} \right) &= \left( \tfrac{8 F_{2} a^{3}}{3 EI}, - \tfrac{2 F_{2}}{EI} a^{2} \right)\end{split}\]

Hierbei ist:

  • \(w_{11}\): Verschiebung bei Position 1, also in Balkenmitte bei \(\xi = \tfrac 1 2,\) aufgrund \(F_1\).

  • \(\psi_{11}\): Neigung bei Position 1 aufgrund \(F_1\).

  • \(w_{21}\): Verschiebung bei Position 2, also rechts bei \(\xi = 1,\) aufgrund \(F_1\).

Lösung

../../../../_images/2.4.2.J_2.png

Einsetzen der Tabellenwerte in die Formeln (1) für \(w\) und (2) \(\psi\) liefert das Ergebnis.

Satz von Betti

Es gilt:

\[w_{12} F_1 = w_{21} F_2\]

vgl. Satz von Maxwell-Betti.

b) Superposition

Berechnen Sie die Querverschiebung \(w_1\) und den Neigungswinkel \(\psi_1\) bei \(F_1\) aufgrund beider Kräfte \(F_1\) und \(F_2.\) Zeigen Sie, dass:

\[\begin{split}w_1 &= w_{11} + w_{12} \\ &= \tfrac{F_{1} a^{3}}{3 EI} + \tfrac{5 F_{2} a^{3}}{6 EI} \\ \psi_1 &= \psi_{11} + \psi_{12}\\ &= - \tfrac{F_{1} a^{2}}{2 EI} - \tfrac{3 F_{2} a^{2}}{2 EI} \\ w_2 &= w_{21} + w_{22} \\ &= \tfrac{5 F_{1} a^{3}}{6 EI} + \tfrac{8 F_{2} a^{3}}{3 EI} \\ \psi_2 &= \psi_{21} + \psi_{22} \\ &= - \tfrac{F_{1} a^{2}}{2 EI} - \tfrac{2 F_{2}}{EI} a^{2}\end{split}\]

Lösung

Einsetzen der Werte aus (2) liefert das Ergebnis.

c) Ergebnis für Größen

Berechnen Sie \(w_2\) in \(\mathrm{mm}\) (Millimeter) für die folgenden Größen:

\[\begin{split}F_1 &= 10 \,\mathrm{kN} \\ F_2 &= 10 \,\mathrm{kN} \\ a &= 1 \,\mathrm{m} \\ E &= 210 \,\mathrm{GPa} \\ I &= 318 \,\mathrm{cm}^4\end{split}\]

Runden Sie auf Rundestellenwert \(0{,}01\). Zeigen Sie, dass:

\[w_2 \stackrel{\small{0{,}01}}{\approx} 52{,}41 \,\mathrm{mm}\]

Lösung

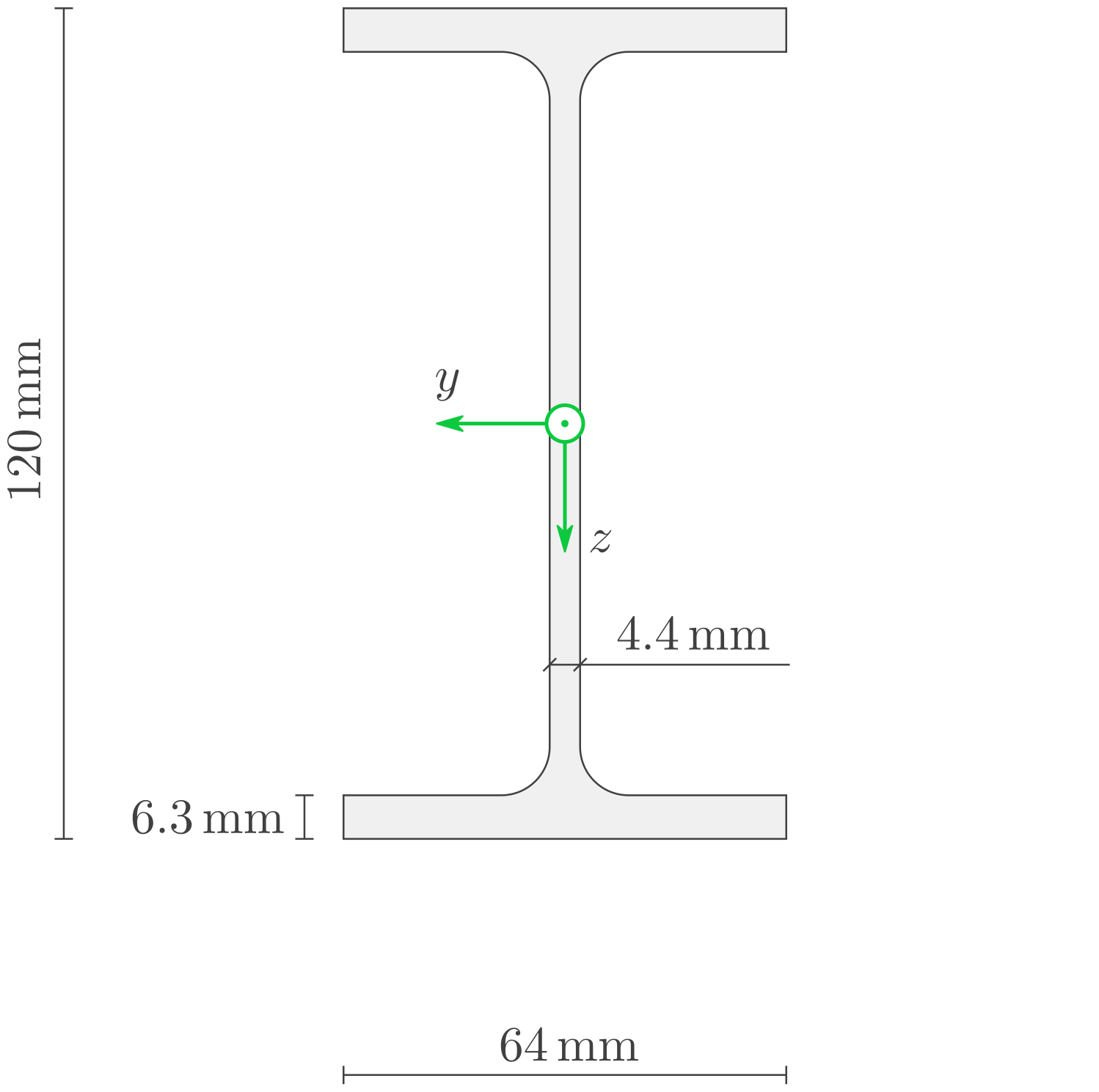
Einsetzen der gegebenen Größen liefert:

\[w_2 \stackrel{0.01}{\approx} 52{,}41 \,\mathrm{mm}\]

Veranschaulichung

  • \(E= 210 \,\mathrm{GPa}\) entspricht dem E-Modul von Stahl.

  • \(I = 318 \,\mathrm{cm}^4\) entspricht dem \(I_{yy}\) eines IPE 120.

    ../../../../_images/ipe_120.png

    DIN 1025-5: IPE 120: \(I_{yy}\stackrel{1.0}{\approx} 318 \,\mathrm{cm}^4\)

  • \(F_1 = F_2 = 10 \,\mathrm{kN}\) entspricht ca. der Gewichtskraft eines VW Polo.

    ../../../../_images/VW_Polo_IV_front_20071106.jpg

    VW Polo: Masse ca. \(1000\,\mathrm{kg}\), Gewichtskraft ca. \(1000\,\mathrm{kg} \cdot 10\,\tfrac{\mathrm{m}}{\mathrm{s}^2} = 10 \,\mathrm{kN}\)

d) Funktionsgraph

Zeichnen Sie für diese Größen \(w\) in \(\mathrm{mm}\) (Millimeter) über \(\tfrac{x}{2a}\).

Zeigen Sie, dass die Gesamtverschiebung gleich ist der Summe von:

  1. der Verschiebung aufgrund \(F_1\) und

  2. der Verschiebung aufgrund \(F_2\).

Lösung

Bokeh Plot

SymPy

Nachfolgend ein Programm, dass Sie ausführen können:

  • Auf dem PC z.B. mit Anaconda.

  • Im Browser (online) in drei Schritten:

    1. Copy: Source Code in die Zwischenablage kopieren.

    2. Paste: Source Code als Python-Notebook einfügen z.B. auf:

    3. Play: Ausführen.

from sympy.physics.units import *
from sympy import *

# Units:
(mm, cm)  =  ( m/1000, m/100 )
kN        =  10**3*newton
Pa        =  newton/m**2
MPa       =  10**6*Pa
GPa       =  10**9*Pa
deg       =  pi/180
half      =  S(1)/2

# Rounding:
import decimal
from decimal import Decimal as DX
from copy import deepcopy
def iso_round(obj, pv,
    rounding=decimal.ROUND_HALF_EVEN):
    import sympy
    """
    Rounding acc. to DIN EN ISO 80000-1:2013-08
    place value = Rundestellenwert
    """
    assert pv in set([
        # place value   #  round to:
        "1",              #  round to integer
        "0.1",            #  1st digit after decimal
        "0.01",           #  2nd
        "0.001",          #  3rd
        "0.0001",         #  4th
        "0.00001",        #  5th
        "0.000001",       #  6th
        "0.0000001",      #  7th
        "0.00000001",     #  8th
        "0.000000001",    #  9th
        "0.0000000001",   # 10th
        ])
    objc = deepcopy(obj)
    try:
        tmp = DX(str(float(objc)))
        objc = tmp.quantize(DX(pv), rounding=rounding)
    except:
        for i in range(len(objc)):
            tmp = DX(str(float(objc[i])))
            objc[i] = tmp.quantize(DX(pv), rounding=rounding)
    return objc

# ---

F1, F2, a, EI = var("F1, F2, a, EI")

def macaulay(x, a, n):
    "https://en.wikipedia.org/wiki/Macaulay_brackets"
    if x < a:
        return 0
    else:
        return (x-a)**n

def w(EI, F, a1, a2, r, xi):
    xi2 = xi*xi
    xi3 = xi*xi*xi
    tmp = F/6/EI
    tmp *= (a1 + a2)**3
    tmp *= 3*xi2*r - xi3 + macaulay(xi,r,3)
    return tmp

def psi(EI, F, a1, a2, r, xi):
    xi2 = xi*xi
    tmp = - F/6/EI
    tmp *= (a1 + a2)**2
    tmp *= 6*xi*r - 3*xi2 + 3*macaulay(xi,r,2)
    return tmp

# Given symbols:
a, EI, F1, F2 = var("a, EI, F1, F2")

tpl_D = {}
tpl_D["11"] = ( F1,   a, a, half, half )
tpl_D["21"] = ( F1,   a, a, half,    1 )
tpl_D["12"] = ( F2, 2*a, 0, half, half )
tpl_D["22"] = ( F2, 2*a, 0, 1,    1    )

w_D = {}
p_D = {}

for x in sorted(tpl_D):
    (F, a1, a2, r, xi) = tpl_D[x]
    w_D[x] =   w(EI, F, a1, a2, r, xi)
    p_D[x] = psi(EI, F, a1, a2, r, xi)

(w1, p1) = (w_D["11"] + w_D["12"], p_D["11"] + p_D["12"])
(w2, p2) = (w_D["21"] + w_D["22"], p_D["21"] + p_D["22"])

pprint("\nw1, ψ1, w2, ψ2:")
pprint(w1)
pprint(p1)
pprint(p2)
pprint(w2)

sub_list = [
    (F1,   10 *kN             ),
    (F2,   10 *kN             ),
    (a,     1 *m              ),
    (EI,  210 *GPa * 318*cm**4), # IPE 120
    ]

pprint("\nw2 / mm:")
tmp = w2.subs(sub_list)
tmp /= mm
tmp = iso_round(tmp,"0.01")
pprint(tmp)

               
w1, ψ1, w2, ψ2:
    3       3
F₁⋅a    F₂⋅a 
───── + ─────
 3⋅EI    3⋅EI
      2       2
  F₁⋅a    F₂⋅a 
- ───── - ─────
   2⋅EI    2⋅EI
      2         2
  F₁⋅a    2⋅F₂⋅a 
- ───── - ───────
   2⋅EI      EI  
      3         3
5⋅F₁⋅a    8⋅F₂⋅a 
─────── + ───────
  6⋅EI      3⋅EI 
        
w2 / mm:
52.41

Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.