3.3.G

Video

Simulation

Handschriftliche Lösung

SymPy

Nachfolgend ein Programm, dass Sie ausführen können:

Auf dem PC z.B. mit Anaconda.
Im Browser (online) in drei Schritten:
1. Copy: Source Code in die Zwischenablage kopieren.
2. Paste: Source Code als Python-Notebook einfügen z.B. auf:
  - JupyterLite oder
  - JupyterLab oder
  - Colab.
3. Play: Ausführen.

from sympy import *

a = var("a", positive=True)
w1 = var("ω₁")

# Equations (1) to (4):
# Shortcut:
xi = sqrt(15)/2
# Unknowns:
vB, vC = var("vʙ, vᴄ")
w2, w3 = var("ω₂, ω₃")

eq1 = Eq(   vB       ,   w1*a        )
eq2 = Eq(   vC       ,   w3*2*a      )
eq3 = Eq( - vC * xi/2, - w2*xi*a     )
eq4 = Eq( - vC / 4   , - vB + w2/2*a )

unks = [vB, vC, w2, w3]
eqns = [eq1, eq2, eq3, eq4]

print("\nEqns. (1)-(4):")
sol = solve(eqns, unks)
for s in sol:
    pprint("\n")
    tmp = str(s)+":"
    pprint(tmp)
    pprint(sol[s])

# Equations (5) to (10):
# Shortcuts
w2, w3 = sol[w2], sol[w3]
xi2, xi3 = w2*w2, w3*w3

# Unknowns:
aBx, aBy = var("aʙx, aʙy")
aCx, aCy = var("aᴄx, aᴄy")
w2p, w3p = var("ω₂', ω₃'")

eq5  = Eq( aBx, -w1*w1*a                   )
eq6  = Eq( aBy, 0                          )
eq7  = Eq( aCx,     - w3p*xi*a + xi3*a/2   )
eq8  = Eq( aCy,     - w3p*a/2  - xi3*xi*a  )
eq9  = Eq( aCx, aBx - w2p*xi*a - xi2*a/2   )
eq10 = Eq( aCy, aBy + w2p*a/2  - xi2*xi*a  )

unks = [aBx, aBy, aCx, aCy, w2p, w3p]
eqns = [eq5, eq6, eq7, eq8, eq9, eq10]

print("\nEqns. (5)-(10):")
sol = solve(eqns, unks)
for s in sol:
    pprint("\n")
    tmp = str(s)+":"
    pprint(tmp)
    pprint(sol[s])

pprint("\n")

Eqns. (1)-(4):

vʙ:
a⋅ω₁

vᴄ:
2⋅a⋅ω₁

ω₂:
ω₁

ω₃:
ω₁

Eqns. (5)-(10):

aʙx:
     2
-a⋅ω₁ 

aʙy:
0

aᴄx:
     2 
-a⋅ω₁  
───────
   2   

aᴄy:
            2 
-17⋅√15⋅a⋅ω₁  
──────────────
      30      

ω₂':
         2 
-2⋅√15⋅ω₁  
───────────
     15    

ω₃':
        2
2⋅√15⋅ω₁ 
─────────
    15   

Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.

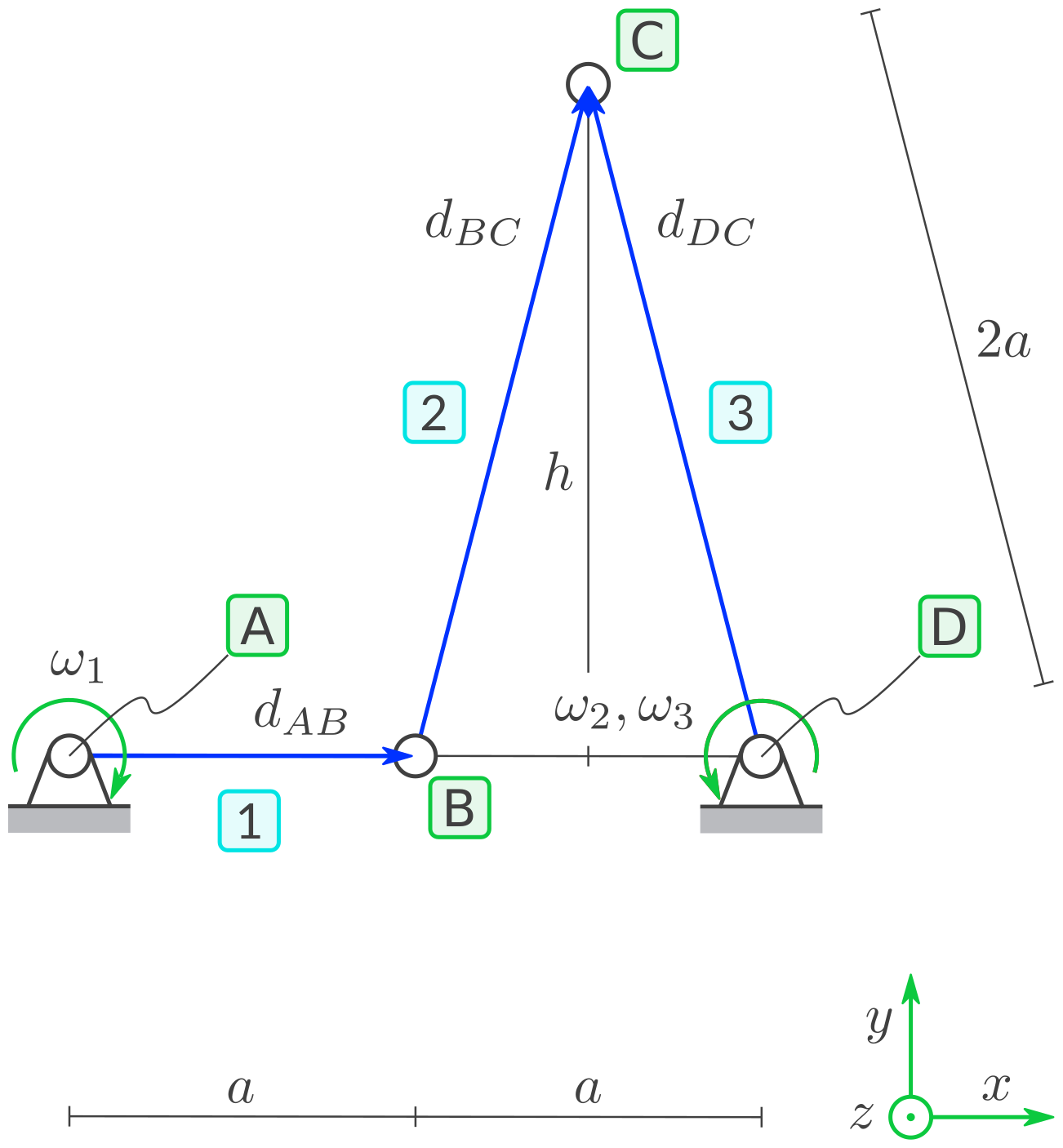
Es geht um ein bewegliches System, das aus drei Starrkörpern besteht. Im betrachteten Zeitpunkt ist das System in der dargestellten Lage.

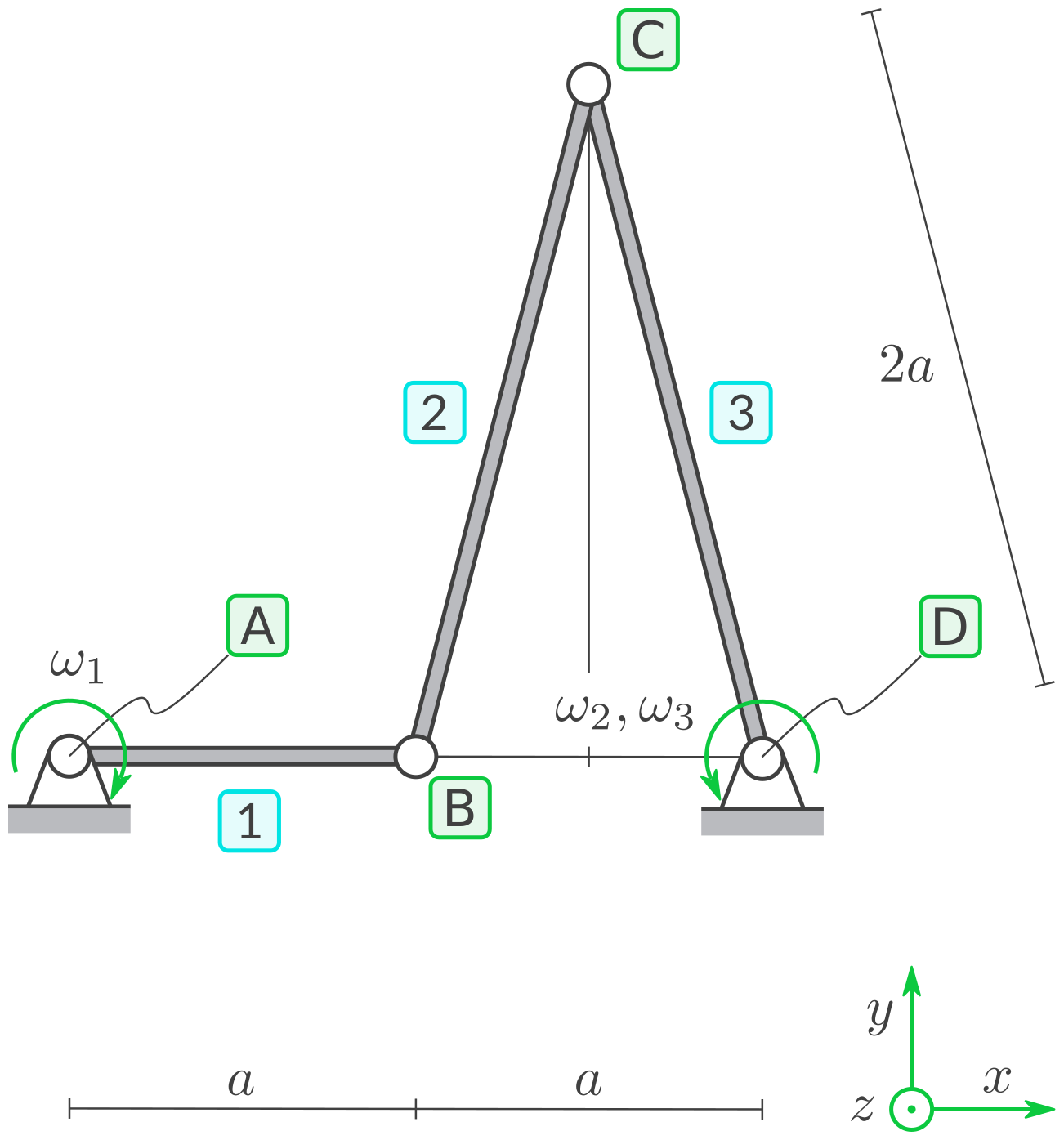
../../../_images/3.3.G.png — Gegebene *Symbole*: \(a, \omega_1, \dot \omega_1 = 0\)

Die Winkelgeschwindigkeiten sind festgelegt als:

\(\omega_1\): Winkelgeschwindigkeit von 1, Zählrichtung \(\circlearrowright\)

\(\omega_2\): Winkelgeschwindigkeit von 2, Zählrichtung \(\circlearrowleft\)

\(\omega_3\): Winkelgeschwindigkeit von 3, Zählrichtung \(\circlearrowleft\)

Untersuchen Sie die Bewegung. Gehen Sie wie folgt vor.

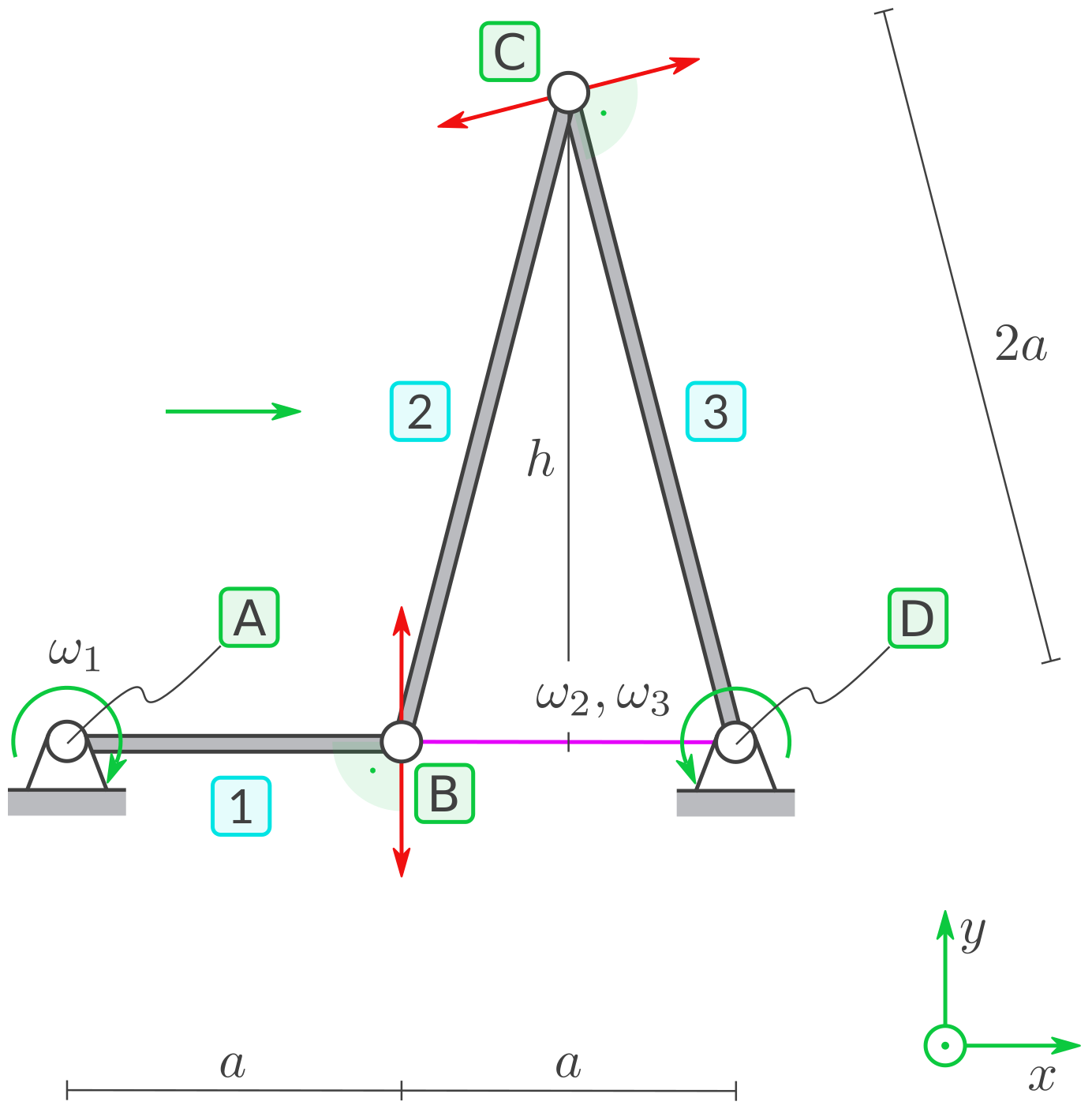
a) Momentanpole

Kennzeichnen Sie die Positionen der Momentanpole der Starrkörper 1, 2 und 3:

Lösung

Starrkörper	Momentanpol
1	A
2	D
3	D

Details

Der MP von 1 ist bei A, weil 1 bei A drehbar gelagert (angepinnt) ist.
Der MP von 3 ist bei D, weil 3 bei D drehbar gelagert (angepinnt) ist.
Der MP von 2 wird berechnet aus den Richtungen der Geschwindigkeiten zweier verschiedener Teilchen auf 2. Diese Teilchen sind: 1. ein Teilchen bei B und 2. ein Teilchen bei C.

Zu 1. zeichnet man eine Gerade bei B, die senkrecht ist zur Geschwindigkeitsrichtung des Teilchens bei B ist. Und zu 2. zeichnet man eine Gerade bei C, die senkrecht ist zur Geschwindigkeitsrichtung des Teilchens bei C. Diese beiden Geraden schneiden sich in einem Punkt - nämlich in D. Und darum ist D der MP von 2.
Der gekrümmte Pfeil für \(\omega_3\) und \(\omega_2\) ist bei D eingetragen, weil D Momentanpol beider Starrkörper ist.

b) Winkelgeschwindigkeiten & Winkelbeschleunigungen

Betrachtung der Starrkörper:

Körper	Winkelgeschwindigkeitsv.	Winkelbeschleunigungsv.
1	\(\boldsymbol \omega_1\)	\(\dot{\boldsymbol \omega_1}\)
2	\(\boldsymbol \omega_2\)	\(\dot{\boldsymbol \omega_2}\)
3	\(\boldsymbol \omega_3\)	\(\dot{\boldsymbol \omega_3}\)

Komponenten dieser Vektoren:

Körper	Winkelgeschwindigkeitsv.-Komp.	Winkelbeschleunigungsv.-Komp.
1	\(\left(\omega_{1x}, \omega_{1y}, \omega_{1z}\right)\)	\(\left(\dot{\omega_{1x}}, \dot{\omega_{1y}}, \dot{\omega_{1z}}\right)\)
2	\(\left(\omega_{2x}, \omega_{2y}, \omega_{2z}\right)\)	\(\left(\dot{\omega_{2x}}, \dot{\omega_{2y}}, \dot{\omega_{2z}}\right)\)
3	\(\left(\omega_{3x}, \omega_{3y}, \omega_{3z}\right)\)	\(\left(\dot{\omega_{3x}}, \dot{\omega_{3y}}, \dot{\omega_{3z}}\right)\)

Für jeden Körper gibt es formal 6 Vektor-Komponenten: 3 für die Winkelgeschwindigkeit und 3 für die Winkelbeschleunigung. In 2D sind aber jeweils zwei Komponenten Null. Und für die jeweils dritte (hier die \(z\)-Komponente) wird:

mit einem Pfeil die Zählrichtung definiert und
eine Bezeichnung definiert (hier \(\omega_1, \omega_2, \omega_3\) bzw. \(\dot \omega_1, \dot \omega_2, \dot \omega_3\)).

Tragen Sie die fehlenden Werte ein:

\[\begin{split}\begin{bmatrix} \omega_{1x}\\ \omega_{1y}\\ \omega_{1z} \end{bmatrix} &= \begin{bmatrix} 0\\ 0\\ -\omega_1 \end{bmatrix} \\ \begin{bmatrix} \dot{\omega_{1x}}\\ \dot{\omega_{1y}}\\ \dot{\omega_{1z}} \end{bmatrix} &= \begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix} \\ \begin{bmatrix} \omega_{2x}\\ \omega_{2y}\\ \omega_{2z} \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ \ldots \end{bmatrix}\end{split}\]

\[\begin{split}\begin{bmatrix} \dot{\omega_{2x}} \\ \dot{\omega_{2y}} \\ \dot{\omega_{2z}} \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ \ldots \end{bmatrix} \\ \begin{bmatrix} \omega_{3x}\\ \omega_{3y}\\ \omega_{3z} \end{bmatrix} &= \begin{bmatrix} \ldots \\ \ldots \\ \ldots \end{bmatrix} \\ \begin{bmatrix} \dot{\omega_{3x}}\\ \dot{\omega_{3y}}\\ \dot{\omega_{3z}} \end{bmatrix} &= \begin{bmatrix} \ldots \\ \ldots \\ \ldots \end{bmatrix}\end{split}\]

Und notieren Sie die vier Unbekannten, die berechnet werden müssen.

Lösung

\[\begin{split}\begin{bmatrix} \omega_{1x}\\ \omega_{1y}\\ \omega_{1z} \end{bmatrix} &= \begin{bmatrix} 0\\ 0\\ -\omega_1 \end{bmatrix} \\ \begin{bmatrix} \dot{\omega_{1x}}\\ \dot{\omega_{1y}}\\ \dot{\omega_{1z}} \end{bmatrix} &= \begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix} \\ \begin{bmatrix} \omega_{2x}\\ \omega_{2y}\\ \omega_{2z} \end{bmatrix} &= \begin{bmatrix} 0\\ 0\\ \omega_2 \end{bmatrix} \\ \begin{bmatrix} \dot{\omega_{2x}}\\ \dot{\omega_{2y}}\\ \dot{\omega_{2z}} \end{bmatrix} &= \begin{bmatrix} 0\\ 0\\ \dot{\omega_2} \end{bmatrix} \\ \begin{bmatrix} \omega_{3x}\\ \omega_{3y}\\ \omega_{3z} \end{bmatrix} &= \begin{bmatrix} 0\\ 0\\ \omega_3 \end{bmatrix} \\ \begin{bmatrix} \dot{\omega_{3x}}\\ \dot{\omega_{3y}}\\ \dot{\omega_{3z}} \end{bmatrix} &= \begin{bmatrix} 0\\ 0\\ \dot{\omega_3} \end{bmatrix}\end{split}\]

4 unbekannte Winkelgeschwindigkeitsv.-Komponenten:

\(\left(\omega_2, \dot{\omega_2}\right)\)
\(\left(\omega_3, \dot{\omega_3}\right)\)

c) Geschwindigkeiten & Beschleunigungen

Betrachtung der Teilchen:

Teilchen	Geschwindigkeitsvektor	Beschleunigungsvektor
A	\(\boldsymbol v_A\)	\(\boldsymbol a_A\)
B	\(\boldsymbol v_B\)	\(\boldsymbol a_B\)
C	\(\boldsymbol v_C\)	\(\boldsymbol a_C\)
D	\(\boldsymbol v_D\)	\(\boldsymbol a_D\)

Teilchen	Geschwindigkeitsv.-Komp.	Beschleunigungsv.-Komp.
A	\(\left(v_{Ax}, v_{Ay}, v_{Az}\right)\)	\(\left(a_{Ax}, a_{Ay}, a_{Az}\right)\)
B	\(\left(v_{Bx}, v_{By}, v_{Bz}\right)\)	\(\left(a_{Bx}, a_{By}, a_{Bz}\right)\)
C	\(\left(v_{Cx}, v_{Cy}, v_{Cz}\right)\)	\(\left(a_{Cx}, a_{Cy}, a_{Cz}\right)\)
D	\(\left(v_{Dx}, v_{Dy}, v_{Dz}\right)\)	\(\left(a_{Dx}, a_{Dy}, a_{Dz}\right)\)

Die \(z\)-Komponenten aller Vektoren Null. Und Teilchen bei A und B sind angepinnt, so dass deren Geschwindigkeit und Beschleunigung gleich Null ist. Es bleiben die Teilchen B und C. Da es hier um eine Bewegung in der \((x,y)\)-Ebene gibt, sind alle \(z\)-Komponenten gleich Null,

Es bleiben acht Symbole, die berechnet werden müssen - bzw. ausgedrückt abhängig von den gegebenen Symbolen. Geben Sie diese acht Unbekannten an.

Lösung

Teilchen	Geschwindigkeitsv.-Komp.	Beschleunigungsv.-Komp.
A	\(\left(v_{Ax}, v_{Ay}, v_{Az}\right)=\left(0,0,0\right)\)	\(\left(a_{Ax}, a_{Ay}, a_{Az}\right)=\left(0,0,0\right)\)
B	\(\left(v_{Bx}, v_{By}, v_{Bz}\right)=\left(v_{Bx},v_{By},0\right)\)	\(\left(a_{Bx}, a_{By}, a_{Bz}\right)=\left(a_{Bx},a_{By},0\right)\)
C	\(\left(v_{Cx}, v_{Cy}, v_{Cz}\right)=\left(v_{Cx},v_{Cy},0\right)\)	\(\left(a_{Cx}, a_{Cy}, a_{Cz}\right)=\left(a_{Cx}, a_{Cy},0\right)\)
D	\(\left(v_{Dx}, v_{Dy}, v_{Dz}\right)=\left(0,0,0\right)\)	\(\left(a_{Dx}, a_{Dy}, a_{Dz}\right)=\left(0,0,0\right)\)

8 unbekannte Geschwindigkeits- und Beschleunigungsv.-Komponenten:

\(\left(v_{Bx}, v_{By}\right), \left(a_{Bx}, a_{By}\right)\)
\(\left(v_{Cx}, v_{Cy}\right), \left(a_{Cx}, a_{Cy}\right)\)

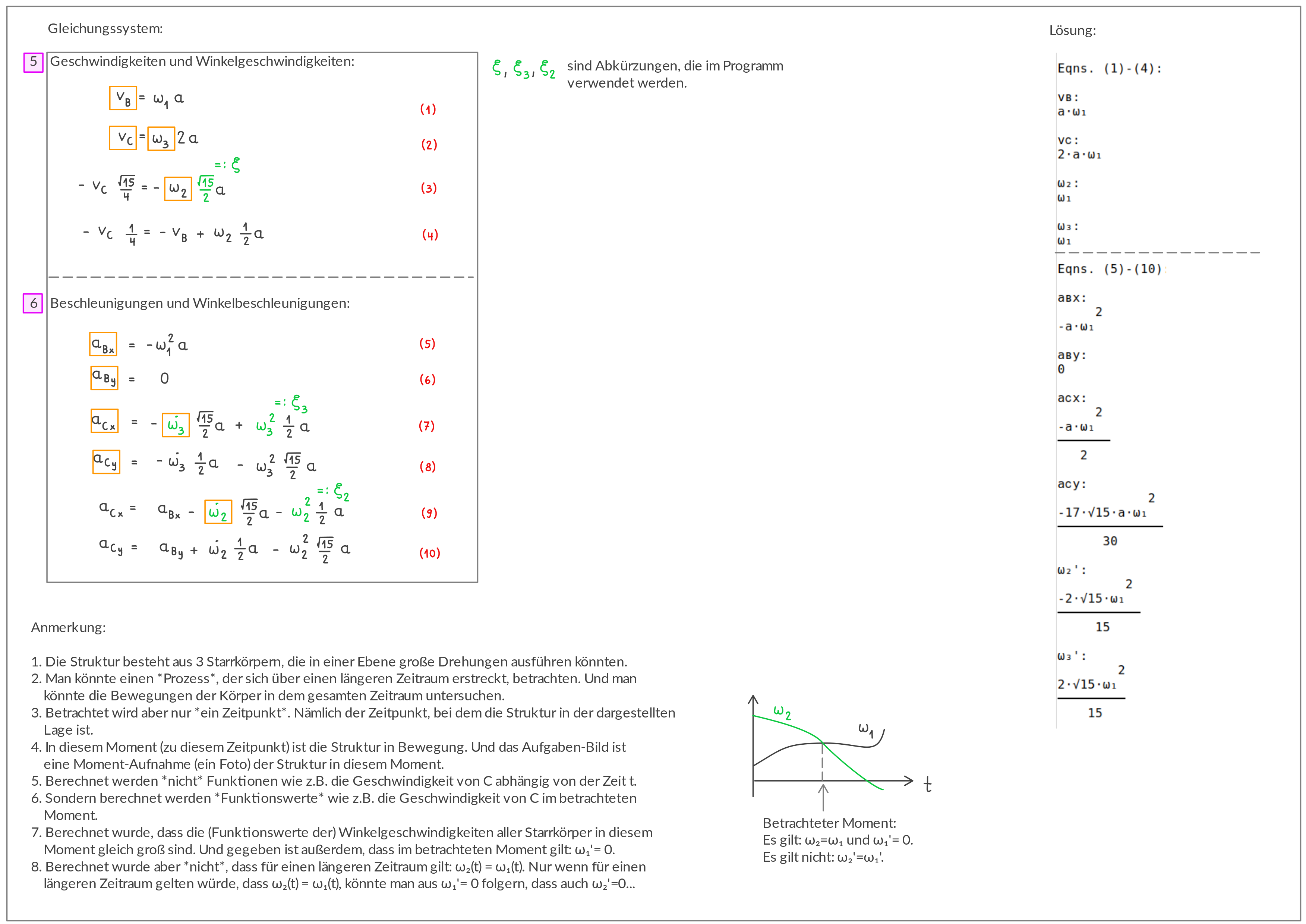
Insgesamt gibt es 12 Unbekannte. Und ab hier werden diese 12 Unbekannten berechnet:

Winkelgeschwindigkeiten und Geschwindigkeiten: \(\omega_2, \omega_3, \left(v_{Bx}, v_{By}\right), \left(v_{Cx}, v_{Cy}\right)\)
Winkelbeschleunigungen und Beschleunigungen: \(\dot{\omega_2}, \dot{\omega_3}, \left(a_{Bx}, a_{By}\right), \left(a_{Cx}, a_{Cy}\right)\)

d) \(\left(v_{Bx}, v_{By}\right)\) und \(\left(a_{Bx}, a_{By}\right)\)

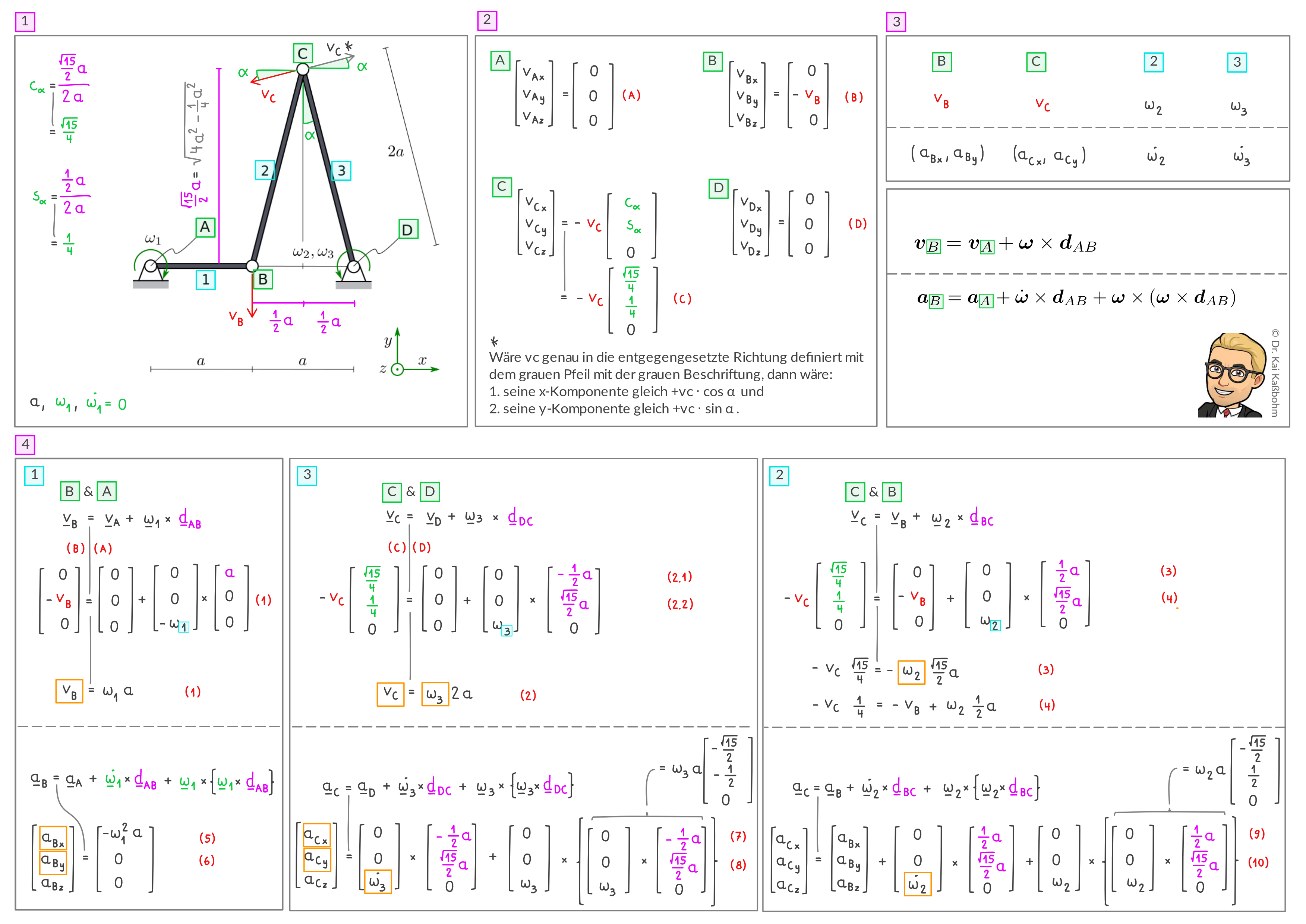
Verwenden Sie die Formeln aus Starrkörper-Kinematik 2D für Starrkörper 1, um die \((x,y,z)\)-Komponenten des Geschwindigkeitsvektors und Beschleunigungsvektors eines Teilchens bei B zu berechnen:

\[\begin{split}\begin{bmatrix} v_{Bx} \\ v_{By} \\ v_{Bz} \end{bmatrix} &= \begin{bmatrix} \dots \\ \dots \\ 0 \end{bmatrix} \quad,\quad \begin{bmatrix} a_{Bx} \\ a_{By} \\ a_{Bz} \end{bmatrix} = \begin{bmatrix} \dots \\ \dots \\ 0 \end{bmatrix}\end{split}\]

Lösung

Körper	Winkelgeschwindigkeit	Teilchen 1	Teilchen 2
1	\(\boldsymbol \omega_1\)	A	B

\[\begin{split}\boldsymbol v_B &= \boldsymbol v_A + \boldsymbol \omega_1 \times \boldsymbol d_{AB} \\ \boldsymbol a_B &= \boldsymbol a_A + \dot{\boldsymbol \omega_1} \times \boldsymbol d_{AB} + \boldsymbol\omega_1 \times \left(\boldsymbol\omega_1 \times \boldsymbol d_{AB}\right)\end{split}\]

Laut Aufgabenstellung ist \(\boldsymbol v_A= \boldsymbol a_A=\dot{\boldsymbol \omega_1}= \boldsymbol 0\). Außerdem ist \(v_{Bz}=a_{Bz}=0\) sowie:

\[\begin{split}\begin{bmatrix} d_{ABx} \\ d_{ABy} \\ d_{ABz} \end{bmatrix} = \begin{bmatrix} a \\ 0 \\ 0 \end{bmatrix}\end{split}\]

Dies führt auf:

\begin{align*} \begin{bmatrix} v_{Bx} \\ v_{By} \\ 0 \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ -\omega_1 \end{bmatrix} \times \begin{bmatrix} a \\ 0 \\ 0 \\ \end{bmatrix} \tag{1a} \\ &= \begin{bmatrix} 0\\ -a \omega_1 \\ 0 \\ \end{bmatrix} \tag{1a'} \\ \\ \begin{bmatrix} a_{Bx} \\ a_{By} \\ 0 \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \times \begin{bmatrix} a \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ -\omega_1 \end{bmatrix} \times \left\{ \begin{bmatrix} 0\\ 0\\ -\omega_1 \end{bmatrix} \times \begin{bmatrix} a \\ 0 \\ 0 \end{bmatrix} \right\} \tag{1b} \\ &= \begin{bmatrix} 0\\ 0\\ -\omega_1 \end{bmatrix} \times \begin{bmatrix} 0\\ -a \omega_1 \\ 0\\ \end{bmatrix} \tag{1b'} \\ &= \begin{bmatrix} -a\omega_1^2 \\ 0\\ 0\\ \end{bmatrix} \tag{1b''} \end{align*}

Die ersten beiden Zeilen von (1a) sind zwei Gleichungen zur Berechnung der zwei Unbekannten \(v_{Bx}, v_{By}\).
Die ersten beiden Zeilen von (1b) sind zwei Gleichungen zur Berechnung der zwei Unbekannten \(a_{Bx}, a_{By}\).

Umformen und Auflösen nach den Unbekannten führt auf:

\[\begin{split}\begin{bmatrix} v_{Bx} \\ v_{By} \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ - a \omega_1 \\ 0 \end{bmatrix} \quad,\quad \begin{bmatrix} a_{Bx} \\ a_{By} \\ 0 \end{bmatrix} = \begin{bmatrix} - a \omega_1^2 \\ 0 \\ 0 \end{bmatrix}\end{split}\]

Ab hier ist die Geschwindigkeit und Beschleunigung von B bekannt.

Verbleibende 8 unbekannte Komponenten:

Winkelgeschwindigkeiten und Geschwindigkeiten: \(\omega_2, \omega_3, \left(v_{Cx}, v_{Cy}\right)\)
Winkelbeschleunigungen und Beschleunigungen: \(\dot{\omega_2}, \dot{\omega_3}, \left(a_{Cx}, a_{Cy}\right)\)

e) Berechnung der verbleibenden Unbekannten

Verwenden Sie die Formeln aus Starrkörper-Kinematik 2D für Starrkörper 2 und 3. Berechnen Sie Geschwindigkeit und Beschleunigung von C und die Winkelgeschwindigkeiten und Winkelbeschleunigungen der Starrkörper 2 und 3.

Lösung

Körper	Winkelgeschwindigkeit	Teilchen 1	Teilchen 2
2	\(\boldsymbol \omega_2\)	B	C
3	\(\boldsymbol \omega_3\)	D	C

\[\begin{split}\boldsymbol v_C &= \boldsymbol v_B + \boldsymbol \omega_2 \times \boldsymbol d_{BC} \\ \boldsymbol a_C &= \boldsymbol a_B + \dot{\boldsymbol \omega_2} \times \boldsymbol d_{BC} + \boldsymbol\omega_2 \times \left(\boldsymbol\omega_2 \times \boldsymbol d_{BC}\right) \\ \boldsymbol v_C &= \boldsymbol v_D + \boldsymbol \omega_3 \times \boldsymbol d_{DC} \\ \boldsymbol a_C &= \boldsymbol a_D + \dot{\boldsymbol \omega_3} \times \boldsymbol d_{DC} + \boldsymbol\omega_3 \times \left(\boldsymbol\omega_3 \times \boldsymbol d_{DC}\right)\end{split}\]

Laut Aufgabenstellung ist \(\boldsymbol v_B, \boldsymbol a_B, \boldsymbol v_D=\boldsymbol a_D=\boldsymbol 0\). Außerdem ist:

\[\begin{split}\begin{bmatrix} d_{BCx} \\ d_{BCy} \\ d_{BCz} \end{bmatrix} = \begin{bmatrix} \tfrac12 a \\ h \\ 0 \end{bmatrix} \quad,\quad \begin{bmatrix} d_{DCx} \\ d_{DCy} \\ d_{DCz} \end{bmatrix} = \begin{bmatrix} - \tfrac12 a \\ h \\ 0 \end{bmatrix}\end{split}\]

wobei als Abkürzung definiert wurde:

\[\begin{split}h &= \sqrt{(2a)^2 - (\tfrac12 a)^2} \\ &= a \sqrt{\tfrac{15}{4}} \\ &= \tfrac{a}{2} \sqrt{15}\end{split}\]

Einsetzen liefert:

\begin{align*} \begin{bmatrix} v_{Cx} \\ v_{Cy} \\ 0 \end{bmatrix} &= \begin{bmatrix} 0 \\ - a \omega_1 \\ 0 \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ \omega_2 \end{bmatrix} \times \begin{bmatrix} \tfrac12 a \\ h \\ 0 \end{bmatrix} \tag{2a} \\ \begin{bmatrix} a_{Cx} \\ a_{Cy} \\ 0 \end{bmatrix} &= \begin{bmatrix} - a \omega_1^2 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ \dot{\omega_2} \end{bmatrix} \times \begin{bmatrix} \tfrac12 a \\ h \\ 0 \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ \omega_2 \end{bmatrix} \times \left\{ \begin{bmatrix} 0\\ 0\\ \omega_2 \end{bmatrix} \times \begin{bmatrix} \tfrac12 a \\ h \\ 0 \end{bmatrix} \right\} \tag{2b} \\ \\ \begin{bmatrix} v_{Cx} \\ v_{Cy} \\ 0 \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ \omega_3 \end{bmatrix} \times \begin{bmatrix} - \tfrac12 a \\ h \\ 0 \end{bmatrix} \tag{3a} \\ \begin{bmatrix} a_{Cx} \\ a_{Cy} \\ 0 \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ \dot{\omega_3} \end{bmatrix} \times \begin{bmatrix} - \tfrac12 a \\ h \\ 0 \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ \omega_3 \end{bmatrix} \times \left\{ \begin{bmatrix} 0\\ 0\\ \omega_3 \end{bmatrix} \times \begin{bmatrix} -\tfrac12 a \\ h \\ 0 \end{bmatrix} \right\} \tag{3b} \end{align*}

Die jeweils ersten beiden Zeilen von (2a) und (3a) sind vier Gleichungen zur Berechnung der vier Unbekannten Winkelgeschwindigkeiten und Geschwindigkeiten \(\omega_2, \omega_3, \left(v_{Cx}, v_{Cy}\right)\). Umformen dieser Gleichungen führt auf:

\begin{align*} \begin{bmatrix} v_{Cx} \\ v_{Cy} \\ 0 \end{bmatrix} &= \begin{bmatrix} 0 \\ - a \omega_1 \\ 0 \end{bmatrix} + \begin{bmatrix} - h \omega_2\\ \tfrac a 2 \omega_2 \\ 0 \\ \end{bmatrix} \tag{2a'} \\ &= \begin{bmatrix} - h \omega_2\\ - a \omega_1 + \tfrac a 2 \omega_2 \\ 0 \\ \end{bmatrix} \tag{2a''} \\ \\ \begin{bmatrix} v_{Cx} \\ v_{Cy} \\ 0 \end{bmatrix} &= \begin{bmatrix} - h \omega_3\\ - \tfrac a 2 \omega_3\\ 0\\ \end{bmatrix} \tag{3a'} \end{align*}

Auflösen nach den 4 Unbekannten führt auf:

\[\begin{split}\begin{bmatrix} v_{Cx} \\ v_{Cy} \\ 0 \end{bmatrix} &= \begin{bmatrix} - \frac{a \omega_{1}}{2} \sqrt{15}\\ - \frac{a \omega_{1}}{2}\\ 0 \end{bmatrix} \\ \begin{bmatrix} 0\\ 0\\ \omega_2 \end{bmatrix} &= \begin{bmatrix}0\\0\\\omega_{1}\end{bmatrix} \\ \begin{bmatrix} 0\\ 0\\ \omega_3 \end{bmatrix} &= \begin{bmatrix}0\\0\\\omega_{1}\end{bmatrix}\end{split}\]

Details

Lösung von Hand:

\(v_{Cx}\) und \(v_{Cy}\) eliminieren durch Gleichsetzen von (2a‘‘) und (3a‘) führt auf:

\[\begin{split}\begin{bmatrix} - h \omega_2\\ - a \omega_1 + \tfrac a 2 \omega_2 \\ 0 \\ \end{bmatrix} = \begin{bmatrix} - h \omega_3\\ - \tfrac a 2 \omega_3\\ 0\\ \end{bmatrix}\end{split}\]

Umformen führt auf zwei Gleichungen, aus denen man sehr leicht \(\omega_2\) und \(\omega_3\) berechnen kann. Ohne die dritte Zeile ergibt das:

\[\begin{split}\begin{bmatrix} - \omega_2\\ - \omega_1 + \tfrac 1 2 \omega_2 \\ \end{bmatrix} = \begin{bmatrix} - \omega_3\\ - \tfrac 1 2 \omega_3\\ \end{bmatrix}\end{split}\]

so dass die Lösung ist:

\[\begin{split}\omega_2 &= \omega_1 \\ \omega_3 &= \omega_1\end{split}\]
Und damit lassen sich leicht \(v_{Cx}\) und \(v_{Cy}\) berechnen.

Die jeweils ersten beiden von (2b) und (3b) sind vier Gleichungen zur Berechnung der vier unbekannten Winkelbeschleunigungen und Beschleunigungen \(\dot{\omega_{2}}, \dot{\omega_{3}}, \left(a_{Cx}, a_{Cy}\right)\). Umformen und Auflösen nach den Unbekannten liefert:

\[\begin{split}\begin{bmatrix} a_{Cx} \\ a_{Cy} \\ 0 \end{bmatrix} &= \begin{bmatrix} - \frac{a \omega_{1}^{2}}{2}\\ - \frac{17 a}{30} \sqrt{15} \omega_{1}^{2}\\ 0 \end{bmatrix} \\ \begin{bmatrix} 0\\ 0\\ \dot{\omega_2} \end{bmatrix} &= \begin{bmatrix}0\\0\\- \tfrac{2 \sqrt{15}}{15} \omega_{1}^{2}\end{bmatrix} \\ \begin{bmatrix} 0\\ 0\\ \dot{\omega_3} \end{bmatrix} &= \begin{bmatrix}0\\0\\\tfrac{2 \sqrt{15}}{15} \omega_{1}^{2}\end{bmatrix}\end{split}\]

Details

Lösung von Hand: (2b) und (3b) sind 4 Gleichungen zur Berechnung der vier Unbekannten \(\dot{\omega_{2}}, \dot{\omega_{3}}, \left(a_{Cx}, a_{Cy}\right)\):

\[\begin{split}\begin{bmatrix} a_{Cx}\\a_{Cy}\\0 \end{bmatrix} &= \begin{bmatrix} - \frac{a \dot{\omega_{2}}}{2} \sqrt{15} - \frac{3 a}{2} \omega_{1}^{2}\\\frac{a \dot{\omega_{2}}}{2} - \frac{\sqrt{15} a}{2} \omega_{1}^{2}\\0 \end{bmatrix} \\ \begin{bmatrix} a_{Cx}\\a_{Cy}\\0\end{bmatrix} &= \begin{bmatrix} - \frac{a \dot{\omega_{3}}}{2} \sqrt{15} + \frac{a \omega_{1}^{2}}{2}\\- \frac{a \dot{\omega_{3}}}{2} - \frac{\sqrt{15} a}{2} \omega_{1}^{2}\\0 \end{bmatrix}\end{split}\]

Eliminieren von \(a_{Cx}\) und \(a_{Cy}\) 2 liefert Gleichungen zur Berechnung der 2 Unbekannten \(\dot{\omega_{2}}, \dot{\omega_{3}}\):

\[\begin{split}\begin{bmatrix} - \frac{a \dot{\omega_{2}}}{2} \sqrt{15} - \frac{3 a}{2} \omega_{1}^{2}\\\frac{a \dot{\omega_{2}}}{2} - \frac{\sqrt{15} a}{2} \omega_{1}^{2}\\0 \end{bmatrix} = \begin{bmatrix} - \frac{a \dot{\omega_{3}}}{2} \sqrt{15} + \frac{a \omega_{1}^{2}}{2}\\- \frac{a \dot{\omega_{3}}}{2} - \frac{\sqrt{15} a}{2} \omega_{1}^{2}\\0 \end{bmatrix}\end{split}\]

f) Ergebnis für Größen

Berechnen Sie die \((x,y,z)\)-Komponenten der Geschwindigkeit eines Teilchens bei C für folgende Größen:

\[\begin{split}a &= 1 \, \mathrm{m} \\ \omega_1 &= \pi / \mathrm{s} \\ &= 180 \, ^\circ / \mathrm{s} \\\end{split}\]

Runden Sie auf Rundestellenwert \(0{,}01.\) Zeigen Sie, dass:

\[\begin{split}\begin{bmatrix} v_{Cx} \\ v_{Cy} \\ 0 \end{bmatrix} \stackrel{\small{0{,}01}}{\approx} \begin{bmatrix} -6{,}08 \\ -1{,}57 \\0\end{bmatrix} \, \tfrac{\mathrm{m}}{\mathrm{s}}\end{split}\]

Lösung

Einsetzen der gegebenen Größen liefert die angegebenen Geschwindigkeitskomponenten.

SymPy

Nachfolgend ein Programm, dass Sie ausführen können:

Auf dem PC z.B. mit Anaconda.
Im Browser (online) in drei Schritten:
1. Copy: Source Code in die Zwischenablage kopieren.
2. Paste: Source Code als Python-Notebook einfügen z.B. auf:
  - JupyterLite oder
  - JupyterLab oder
  - Colab.
3. Play: Ausführen.

from sympy.physics.units import *
from sympy import *

# Units:
(mm, cm)  =  ( m/1000, m/100 )
kN        =  10**3*newton
Pa        =  newton/m**2
MPa       =  10**6*Pa
GPa       =  10**9*Pa
deg       =  pi/180
half      =  S(1)/2

# Rounding:
import decimal
from decimal import Decimal as DX
from copy import deepcopy
def iso_round(obj, pv,
    rounding=decimal.ROUND_HALF_EVEN):
    import sympy
    """
    Rounding acc. to DIN EN ISO 80000-1:2013-08
    place value = Rundestellenwert
    """
    assert pv in set([
        # place value   #  round to:
        "1",              #  round to integer
        "0.1",            #  1st digit after decimal
        "0.01",           #  2nd
        "0.001",          #  3rd
        "0.0001",         #  4th
        "0.00001",        #  5th
        "0.000001",       #  6th
        "0.0000001",      #  7th
        "0.00000001",     #  8th
        "0.000000001",    #  9th
        "0.0000000001",   # 10th
        ])
    objc = deepcopy(obj)
    try:
        tmp = DX(str(float(objc)))
        objc = tmp.quantize(DX(pv), rounding=rounding)
    except:
        for i in range(len(objc)):
            tmp = DX(str(float(objc[i])))
            objc[i] = tmp.quantize(DX(pv), rounding=rounding)
    return objc

a = var("a", positive=True)
w1 = var("omega1")

w2z, w3z = var("w2z, w3z")
a1z, a2z, a3z = var("a1z, alpha2, alpha3")
vBx, vBy = var("vBx, vBy")
aBx, aBy = var("aBx, aBy")
vCx, vCy = var("vCx, vCy")
aCx, aCy = var("aCx, aCy")

sub_list=[
    (a, 1 *m),
    (w1, pi / s),
]

w1 = Matrix([0,0,-w1])
w2 = Matrix([0,0, w2z])
w3 = Matrix([0,0, w3z])

a1 = Matrix([0, 0, 0])
a2 = Matrix([0,0,a2z])
a3 = Matrix([0,0,a3z])

vA = Matrix([0, 0, 0])
aA = Matrix([0, 0, 0])
vB = Matrix([vBx, vBy, 0])
aB = Matrix([aBx, aBy, 0])
vC = Matrix([vCx, vCy, 0])
aC = Matrix([aCx, aCy, 0])
vD = Matrix([0, 0, 0])
aD = Matrix([0, 0, 0])

dAB = Matrix([a, 0, 0])
h = sqrt( (2*a)**2 - (a/2)**2 )
dBC = Matrix([ a/2, h, 0])
dDC = Matrix([-a/2, h, 0])

pprint("\nvB and aB:")
eq1a = Eq( vB, vA + w1.cross(dAB) )
eq1b = Eq( aB, aA + a1.cross(dAB)  + w1.cross(w1.cross(dAB)) )
sol = solve([eq1a, eq1b], [vBx, vBy, aBx, aBy])
vBx, vBy = sol[vBx], sol[vBy]
aBx, aBy = sol[aBx], sol[aBy]
vB = Matrix([vBx, vBy, 0])
aB = Matrix([aBx, aBy, 0])
pprint(vB)
pprint(aB)

pprint("\nvC aC, w2, w3:")
eq2a = Eq( vC, vB + w2.cross(dBC) )
eq3a = Eq( vC, vD + w3.cross(dDC) )
a
sol = solve([eq2a, eq3a], [vCx, vCy, w2z, w3z], dict=True)
sol = sol[0]
pprint(sol)
vCx, vCy = sol[vCx], sol[vCy]
w2z, w3z = sol[w2z], sol[w3z]
vC = Matrix([vCx, vCy, 0])
w2 = Matrix([0,0, w2z])
w3 = Matrix([0,0, w3z])

eq2b = Eq( aC, aB + a2.cross(dBC)  + w2.cross(w2.cross(dBC)) )
eq3b = Eq( aC, aD + a3.cross(dDC)  + w3.cross(w3.cross(dDC)) )

pprint("\n(2b):")
pprint(eq2b)
# pprint(latex(eq2b,**kwargs))
pprint("\n(3b):")
pprint(eq3b)
# pprint(latex(eq3b,**kwargs))


sol = solve([eq2b, eq3b], [aCx, aCy, a2z, a3z], dict=True)
sol = sol[0]
pprint(sol)
aCx, aCy = sol[aCx], sol[aCy]
a2z, a3z = sol[a2z], sol[a3z]

aC = Matrix([aCx, aCy, 0])
a2 = Matrix([0,0,a2z])
a3 = Matrix([0,0,a3z])
pprint(vC)
pprint(aC)

pprint(w2)
pprint(w3)
pprint("\na2 and a3:")
pprint(a2)
pprint(a3)

pprint("\nvC / (m/s):")
tmp = vC.subs(sub_list)
tmp /= m/s
tmp = iso_round(tmp,"0.01")
pprint(tmp)

          
vB and aB:
⎡  0  ⎤
⎢     ⎥
⎢-a⋅ω₁⎥
⎢     ⎥
⎣  0  ⎦
⎡     2⎤
⎢-a⋅ω₁ ⎥
⎢      ⎥
⎢  0   ⎥
⎢      ⎥
⎣  0   ⎦
              
vC aC, w2, w3:
⎧     -√15⋅a⋅ω₁        -a⋅ω₁                   ⎫
⎨vCx: ──────────, vCy: ──────, w2z: ω₁, w3z: ω₁⎬
⎩         2              2                     ⎭
     
(2b):
        ⎡                   2⎤
        ⎢  √15⋅a⋅α₂   3⋅a⋅ω₁ ⎥
        ⎢- ──────── - ───────⎥
⎡aCx⎤   ⎢     2          2   ⎥
⎢   ⎥   ⎢                    ⎥
⎢aCy⎥ = ⎢                 2  ⎥
⎢   ⎥   ⎢  a⋅α₂   √15⋅a⋅ω₁   ⎥
⎣ 0 ⎦   ⎢  ──── - ─────────  ⎥
        ⎢   2         2      ⎥
        ⎢                    ⎥
        ⎣         0          ⎦
     
(3b):
        ⎡                 2⎤
        ⎢  √15⋅a⋅α₃   a⋅ω₁ ⎥
        ⎢- ──────── + ─────⎥
⎡aCx⎤   ⎢     2         2  ⎥
⎢   ⎥   ⎢                  ⎥
⎢aCy⎥ = ⎢                 2⎥
⎢   ⎥   ⎢  a⋅α₃   √15⋅a⋅ω₁ ⎥
⎣ 0 ⎦   ⎢- ──── - ─────────⎥
        ⎢   2         2    ⎥
        ⎢                  ⎥
        ⎣        0         ⎦
⎧          2                    2                2               2⎫
⎪     -a⋅ω₁         -17⋅√15⋅a⋅ω₁        -2⋅√15⋅ω₁        2⋅√15⋅ω₁ ⎪
⎨aCx: ───────, aCy: ──────────────, α₂: ───────────, α₃: ─────────⎬
⎪        2                30                 15              15   ⎪
⎩                                                                 ⎭
⎡-√15⋅a⋅ω₁ ⎤
⎢──────────⎥
⎢    2     ⎥
⎢          ⎥
⎢  -a⋅ω₁   ⎥
⎢  ──────  ⎥
⎢    2     ⎥
⎢          ⎥
⎣    0     ⎦
⎡        2     ⎤
⎢   -a⋅ω₁      ⎥
⎢   ───────    ⎥
⎢      2       ⎥
⎢              ⎥
⎢            2 ⎥
⎢-17⋅√15⋅a⋅ω₁  ⎥
⎢──────────────⎥
⎢      30      ⎥
⎢              ⎥
⎣      0       ⎦
⎡0 ⎤
⎢  ⎥
⎢0 ⎥
⎢  ⎥
⎣ω₁⎦
⎡0 ⎤
⎢  ⎥
⎢0 ⎥
⎢  ⎥
⎣ω₁⎦
          
a2 and a3:
⎡     0     ⎤
⎢           ⎥
⎢     0     ⎥
⎢           ⎥
⎢         2 ⎥
⎢-2⋅√15⋅ω₁  ⎥
⎢───────────⎥
⎣     15    ⎦
⎡    0    ⎤
⎢         ⎥
⎢    0    ⎥
⎢         ⎥
⎢        2⎥
⎢2⋅√15⋅ω₁ ⎥
⎢─────────⎥
⎣    15   ⎦
           
vC / (m/s):
⎡-6.08⎤
⎢     ⎥
⎢-1.57⎥
⎢     ⎥
⎣  0  ⎦

Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.