Vektor-Komponenten

Einleitung

• Um die Temperatur eines Teilchens auf einer Linealkante zu beschreiben, braucht man nur eine Zahl mit Einheit \(\mathrm{K}\) (Kelvin).

• Um die Geschwindigkeit eines Teilchens auf einer Linealkante zu beschreiben, braucht man nicht nur eine Zahl mit Einheit \(\tfrac{\mathrm{m}}{\mathrm{s}}\) (Meter pro Sekunde). Sondern man muss auch festlegen, in welcher Richtung man die Geschwindigkeit positiv zählt!

• Man definiert dazu eine Bezugsrichtung (z.B. die Richtung nach rechts auf der Linealkante). Und dann sagt man z.B.: Die Geschwindigkeit des Teilchens nach rechts ist gleich 2 Meter pro Sekunde..

• Jemand, der für sich die Bezugsrichtung nach links festgelegt hat, sagt für dasselbe Teilchen: Die Geschwindigkeit des Teilchens nach links ist gleich minus 2 Meter pro Sekunde..

• Dasselbe jetzt in 2D: Um die Geschwindigkeit eines Teilchens auf einem Tisch zu beschreiben, muss man zwei Richtungen festlegen, in man die Geschwindigkeitskomponenten positiv zählt.

• Als erste Bezugsrichtung kann man z.B. nach rechts festlegen. Und als zweite Bezugsrichtung nach oben.

• Wenn sich ein Teilchen dann von links unten nach rechts oben bewegt, dann gilt für die Komponenten der Teilchen-Geschwindigkeit: Die Komponente nach rechts ist positiv. Und die Komponente nach oben ist auch positiv. Dies gilt aber nur für diese Bezugsrichtungen.

• Jemand, der für sich andere Bezugsrichtungen festgelegt hat, würde andere Komponenten messen für dieselbe Teilchen-Geschwindigkeit.

• Die Komponenten eines Vektors sind also abhängig vom Bezugssystem. Und wenn man die Komponenten in einem Bezugssystem kennt, kann man daraus die Komponenten desselben Vektors in irgendeinem anderen Bezugssystem ausrechnen.

• Man nennt das Passive Transformation von Vektor-Komponenten. Und es ist doch interessant, dass es in der Natur Temperaturen gibt und Geschwindigkeiten… und dass das offenbar ganz unterschiedliche Dinge sind…

Videos

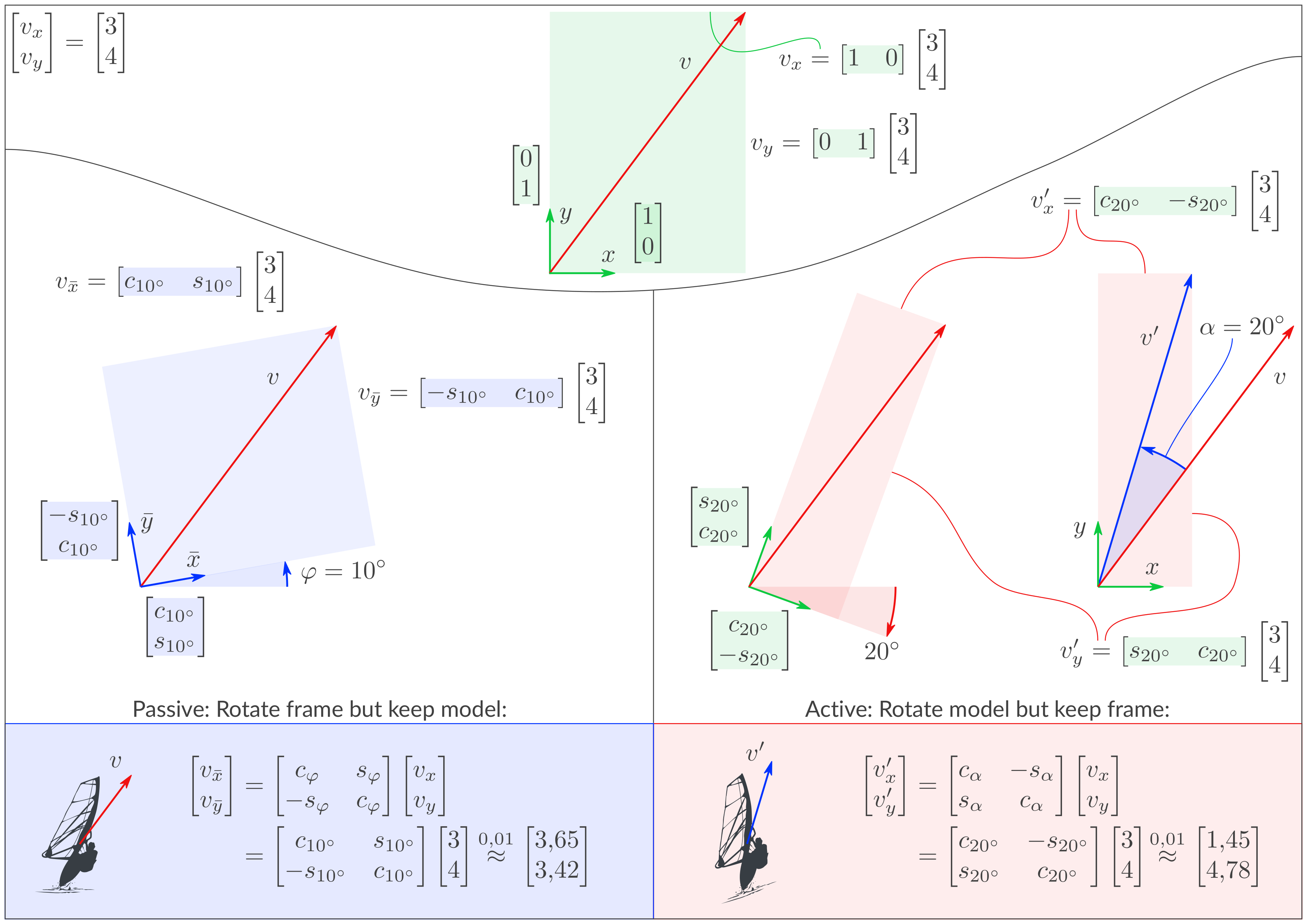
Passive Transformation (links) und Aktive Transformation (rechts).

Symbole

Winkel	zählt pos. um	zeigt Wink.-pos. v.	relativ zu
\(\varphi\)	\(z=\bar z\)	\((\bar x, \bar y)\)	\((x, y)\)
\(\alpha\)	\(z=\bar z\)	\(\boldsymbol v'\)	\(\boldsymbol v\)

Vektor	\((x,y)\)-Komp.	\((\bar x, \bar y)\)-Komp.
\(\boldsymbol v\)	\(\left(v_{x}, v_{y} \right)\)	\(\left( v_{\bar x}, v_{\bar y} \right)\)
\(\boldsymbol v'\)	\(\left(v'_{x}, v'_{y} \right)\)	nicht definiert

Passive und Aktive Transformation

Beispiel-Aufgaben:

• Passive Transformation: M.2.B

• Aktive Transformation: M.2.G

Passive Transformation

1 Vektor & 2 Bezugssysteme:

• \(\left(x, y\right)\)-System: Ist gegeben.

• \(\left(v_{x}, v_{y} \right)\): \(\left(x, y\right)\)-Komponenten des Vektors \(\boldsymbol v\) sind gegeben.

---

• \(\left(\bar x, \bar y\right)\)-System: Ist gedreht relativ zum \((x, y)\)-System um den gegebenen Winkel \(\varphi.\)

• \(\left( v_{\bar x}, v_{\bar y} \right)\): \((\bar x, \bar y)\)-Komponenten des Vektors \(\boldsymbol v\) werden berechnet.

\[\begin{split}\begin{bmatrix} v_{\bar x} \\ v_{\bar y} \end{bmatrix}= \underbrace{ \begin{bmatrix} c_\varphi & s_\varphi \\ -s_\varphi & c_\varphi \end{bmatrix} }_{R_\varphi} \begin{bmatrix} v_x \\ v_y \end{bmatrix}\end{split}\]

Beispiel 1

Sei wie üblich \(x\) nach rechts und \(y\) nach oben, so dass die pos. Zählrichtung für \(\varphi\) entgegen dem Uhrzeigersinn ist.

• \((v_x, v_y)=(3, 0)\): Der rote Vektor zeigt nach rechts und hat Länge 3.

• \(\varphi=90^\circ\): Das blaue System ist relativ zum grünen um \(90^\circ\) entgegen dem Uhrzeigersinn gedreht.

• Die blaue \(\bar x\)-Achse liegt auf der grünen \(y\)-Achse und zeigt nach oben.

• Die blaue \(\bar y\)-Achse zeigt nach links.

\[\begin{split}\begin{bmatrix} v_{\bar x} \\ v_{\bar y} \end{bmatrix} &= \begin{bmatrix} c_{90^\circ} & s_{90^\circ} \\ -s_{90^\circ} & c_{90^\circ} \end{bmatrix} \begin{bmatrix} 3 \\ 0 \end{bmatrix} \\ &= \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \begin{bmatrix} 3 \\ 0 \end{bmatrix} \\ &= \begin{bmatrix} 0 \\ -3 \end{bmatrix}\end{split}\]

Beispiel 2

Sei wie üblich \(x\) nach rechts und \(y\) nach oben.

• \((v_x, v_y)=(0, 4)\)

• \(\varphi=180^\circ\)

• Die blaue \(\bar x\)-Achse zeigt nach links.

• Die blaue \(\bar y\)-Achse zeigt nach unten.

\[\begin{split}\begin{bmatrix} v_{\bar x} \\ v_{\bar y} \end{bmatrix} &= \begin{bmatrix} c_{180^\circ} & s_{180^\circ} \\ -s_{180^\circ} & c_{180^\circ} \end{bmatrix} \begin{bmatrix} 0 \\ 4 \end{bmatrix} \\ &= \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \begin{bmatrix} 0 \\ 4 \end{bmatrix} \\ &= \begin{bmatrix} 0 \\ -4 \end{bmatrix}\end{split}\]

Beispiel 3

• \((v_x, v_y)=(3, 4)\)

• \(\varphi=10^\circ\)

\[\begin{split}\begin{bmatrix} v_{\bar x} \\ v_{\bar y} \end{bmatrix} &= \begin{bmatrix} c_{10^\circ} & s_{10^\circ} \\ -s_{10^\circ} & c_{10^\circ} \end{bmatrix} \begin{bmatrix} 3 \\ 4 \end{bmatrix} \\ &\stackrel{0{,}01}{\approx} \begin{bmatrix} 3{,}65 \\ 3{,}42 \end{bmatrix}\end{split}\]

Vektor-Komponente

Der Anteil eines Vektors in einer bestimmten Richtung (Einheitsvektor \(\boldsymbol e\)) heißt Vektor-Komponente in dieser Richtung:

• Die skalarwertige Vektor-Komponente \(v_e\) in Richtung \(\boldsymbol e\) ist:

  \[v_e = \boldsymbol e \cdot \boldsymbol v\]

• Die vektorwertige Vektor-Komponente \(\boldsymbol v_e\) in Richtung \(\boldsymbol e\) ist:

  \[\boldsymbol v_e = v_e \boldsymbol e\]

Zeigt der Einheitsvektor \(\boldsymbol e\) z.B. in Richtung \(\bar x\) und ist \(\bar x\) wie oben um \(\varphi\) relativ zu \(x\) gedreht: Dann gilt:

\[\begin{split}v_e &= \begin{bmatrix} c_\varphi & s_\varphi \end{bmatrix} \begin{bmatrix} v_x \\ v_y \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} v_{\bar x} \\ v_{\bar y} \end{bmatrix} \\ &= v_{\bar x}\end{split}\]

• \(v_{\bar x}\) ist die skalarwertige Vektor-Komponente in Richtung \(\bar x\).

• \(v_{\bar y}\) ist die skalarwertige Vektor-Komponente in Richtung \(\bar y\).

• \(v_{e}\) ist die skalarwertige Vektor-Komponente in Richtung des Vektors \(\boldsymbol e\).

Aktive Transformation

2 Vektoren & 1 Bezugssystem:

• \(\left(x, y\right)\)-System: Ist gegeben.

• \(\left(v_{x}, v_{y} \right)\): \(\left(x, y\right)\)-Komponenten des Vektors \(\boldsymbol v\) sind gegeben.

---

• Vektor \(\boldsymbol v'\): Ist gedreht relativ zum Vektor \(\boldsymbol v\) um den gegebenen Winkel \(\alpha.\)

• \(\left(v'_{x}, v'_{y} \right)\): \((x, y)\)-Komponenten des Vektors \(\boldsymbol v'\) werden berechnet.

\[\begin{split}\begin{bmatrix} v'_{x} \\ v'_{y} \end{bmatrix} = \begin{bmatrix} c_\alpha & -s_\alpha \\ s_\alpha & c_\alpha \end{bmatrix} \begin{bmatrix} v_x \\ v_y \end{bmatrix}\end{split}\]

Beispiel 1

Sei wie üblich \(x\) nach rechts und \(y\) nach oben, so dass die pos. Zählrichtung für \(\alpha\) entgegen dem Uhrzeigersinn ist.

• \((v_x, v_y)=(0, 4)\)

• \(\alpha=90^\circ\)

• Der rote Vektor \(\boldsymbol v\) zeigt nach oben.

• Der blaue Vektor \(\boldsymbol v'\) ist um \(90^\circ\) entgegen dem Uhrzeigersinn relativ zum roten Vektor gedreht und zeigt darum nach links.

\[\begin{split}\begin{bmatrix} v'_{x} \\ v'_{y} \end{bmatrix} &= \begin{bmatrix} c_{90^\circ} & -s_{90^\circ} \\ s_{90^\circ} & c_{90^\circ} \end{bmatrix} \begin{bmatrix} 0 \\ 4 \end{bmatrix} \\ &= \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 0 \\ 4 \end{bmatrix} \\ &= \begin{bmatrix} -4 \\ 0 \end{bmatrix}\end{split}\]

Beispiel 2

Sei \(x\) und \(y\) wie üblich.

• \((v_x, v_y)=(0, 4)\)

• \(\alpha=-90^\circ\)

• Der rote Vektor \(\boldsymbol v\) zeigt nach oben.

• Der blaue Vektor ist um \(\alpha=-90^\circ\) entgegen dem Uhrzeigersinn relativ zum roten Vektor gedreht - also um \(90^\circ\) im Uhrzeigersinn. Er zeigt darum nach rechts.

\[\begin{split}\begin{bmatrix} v'_{x} \\ v'_{y} \end{bmatrix} &= \begin{bmatrix} c_{-90^\circ} & -s_{-90^\circ} \\ s_{-90^\circ} & c_{-90^\circ} \end{bmatrix} \begin{bmatrix} 0 \\ 4 \end{bmatrix} \\ &= \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \begin{bmatrix} 0 \\ 4 \end{bmatrix} \\ &= \begin{bmatrix} 4 \\ 0 \end{bmatrix}\end{split}\]

Beispiel 3

Sei \(x\) und \(y\) wie üblich.

• \((v_x, v_y)=(3, 4)\)

• \(-\alpha=10^\circ\) bzw. gleichbedeutend \(\alpha=-10^\circ\)

• Der blaue Vektor ist um \(10^\circ\) im Uhrzeigersinn relativ zum roten Vektor gedreht.

\[\begin{split}\begin{bmatrix} v'_{x} \\ v'_{y} \end{bmatrix} &= \begin{bmatrix} c_{-10^\circ} & -s_{-10^\circ} \\ s_{-10^\circ} & c_{-10^\circ} \end{bmatrix} \begin{bmatrix} 3 \\ 4 \end{bmatrix} \\ &\stackrel{0{,}01}{\approx} \begin{bmatrix} 3{,}65 \\ 3{,}42 \end{bmatrix}\end{split}\]

Zusammenhang zwischen Passiver und Aktiver Transformation

\(\alpha=-\varphi\) bzw. gleichbedeutend \(\varphi = - \alpha\) liefert:

\[\begin{split}\begin{bmatrix} v_{\bar x} \\ v_{\bar y} \end{bmatrix} = \begin{bmatrix} v'_{x} \\ v'_{y} \end{bmatrix}\end{split}\]

• Eine passive Transformation mit \(\varphi=30^\circ\) führt auf dieselben transformierten Komponenten wie eine aktive Transformation (desselben Vektors) mit \(\alpha = -30^\circ\).

• Das Bezugssystem um 30 Grad entgegen dem Uhrzeigersinn zu drehen führt auf dieselben transformierten Komponenten wie den Vektor um 30 Grad im Uhrzeigersinn zu drehen.

• Die transformierten Komponenten sind hierbei zahlenmäßig gleich - haben dabei aber verschiedene Bedeutungen.

360-Grad-Periodizität

Passive und Aktive Transformation sind definiert für jeden beliebigen Winkel \(\varphi\) bzw. \(\alpha\). Denn es gilt für jedes beliebige \(n\in\mathbb{N}:\)

\[\begin{split}v_{\bar x}(\varphi\pm n \cdot 360^\circ) &= v_{\bar x}(\varphi) \\ v_{\bar y}(\varphi\pm n \cdot 360^\circ) &= v_{\bar y}(\varphi) \\ \\ v'_{x}(\alpha\pm n \cdot 360^\circ) &= v'_{x}(\alpha) \\ v'_{y}(\alpha\pm n \cdot 360^\circ) &= v'_{y}(\alpha) \\\end{split}\]

Beispiele:

\[\begin{split}v_{\bar x}(100^\circ) &= v_{\bar x}(-260^\circ) \\ v'_{y}(0^\circ) &= v'_{y}(360^\circ)\end{split}\]

SymPy

Nachfolgend ein Programm, dass Sie ausführen können:

• Auf dem PC z.B. mit Anaconda.

• Im Browser (online) in drei Schritten:

  1. Copy: Source Code in die Zwischenablage kopieren.

  2. Paste: Source Code als Python-Notebook einfügen z.B. auf:

     • JupyterLite oder

     • JupyterLab oder

     • Colab.

  3. Play: Ausführen.

from sympy.physics.units import *
from sympy import *

deg  =  pi/180

# Rounding:
import decimal
from decimal import Decimal as DX
from copy import deepcopy
def iso_round(obj, pv,
    rounding=decimal.ROUND_HALF_EVEN):
    import sympy
    """
    Rounding acc. to DIN EN ISO 80000-1:2013-08
    place value = Rundestellenwert
    """
    assert pv in set([
        # place value   #  round to:
        "1",              #  round to integer
        "0.1",            #  1st digit after decimal
        "0.01",           #  2nd
        "0.001",          #  3rd
        "0.0001",         #  4th
        "0.00001",        #  5th
        "0.000001",       #  6th
        "0.0000001",      #  7th
        "0.00000001",     #  8th
        "0.000000001",    #  9th
        "0.0000000001",   # 10th
        ])
    objc = deepcopy(obj)
    try:
        tmp = DX(str(float(objc)))
        objc = tmp.quantize(DX(pv), rounding=rounding)
    except:
        for i in range(len(objc)):
            tmp = DX(str(float(objc[i])))
            objc[i] = tmp.quantize(DX(pv), rounding=rounding)
    return objc

# ---

# For output only:
vbx, vby = var("vx\u0304, vy\u0304")
vpx, vpy = var("v'x, v'y")
vb = Matrix([vbx, vby])
vp = Matrix([vpx, vpy])

# Output precision:
prec = "0.01"

def print_angle(angle):
    pprint("Angle / deg:")
    tmp = angle
    tmp /= deg
    tmp = iso_round(tmp,prec)
    pprint(tmp)
    

def get_R(angle, passive=True):
    c, s = cos(angle), sin(angle)
    R = Matrix([[c, s],[-s, c]])
    if passive == True:
        pprint("\nPassive Transformation")
        print_angle(angle)
        return R
    else:
        pprint("\nActive Transformation")
        print_angle(angle)
        return R.transpose()

pprint("\nv:")
v = Matrix([3 ,4])
pprint(v)

phi = 10 * deg
R = get_R(phi, passive=True)
pprint(vb)
tmp = R*v
tmp = iso_round(tmp,prec)
pprint(tmp)

alpha = 20 * deg
R = get_R(alpha, passive=False)
pprint(vp)
tmp = R*v
tmp = iso_round(tmp,prec)
pprint(tmp)

  
v:
⎡3⎤
⎢ ⎥
⎣4⎦
                      
Passive Transformation
Angle / deg:
10.00
⎡vx̄⎤
⎢  ⎥
⎣vȳ⎦
⎡3.65⎤
⎢    ⎥
⎣3.42⎦
                     
Active Transformation
Angle / deg:
20.00
⎡v'x⎤
⎢   ⎥
⎣v'y⎦
⎡1.45⎤
⎢    ⎥
⎣4.78⎦

Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.

Web-App

Anleitung

• Oben die Komponenten \((v_x, v_y)\) eintragen als einheitenlose Größen. Falls z.B. ein Vektor untersucht werden soll mit den Komponenten \(\left(3\,\tfrac{\mathrm{m}}{\mathrm{s}}, 4 \,\tfrac{\mathrm{m}}{\mathrm{s}}\right)\): Dann würde man oben eintragen: \((v_x, v_y) = (3, 4).\)

• Unten am Schieberegler den Winkel \(\varphi\) oder \(-\alpha\) (jeweils in Grad) einstellen.

• Im Diagramm die transformierten Komponenten \((v_{\bar x}, v_{\bar y})\) oder \((v'_x, v'_y)\) ablesen.

3D

Bemerkung

Für 3D siehe 3D-Drehungen.