Herleitung klassisch
Voraussetzungen
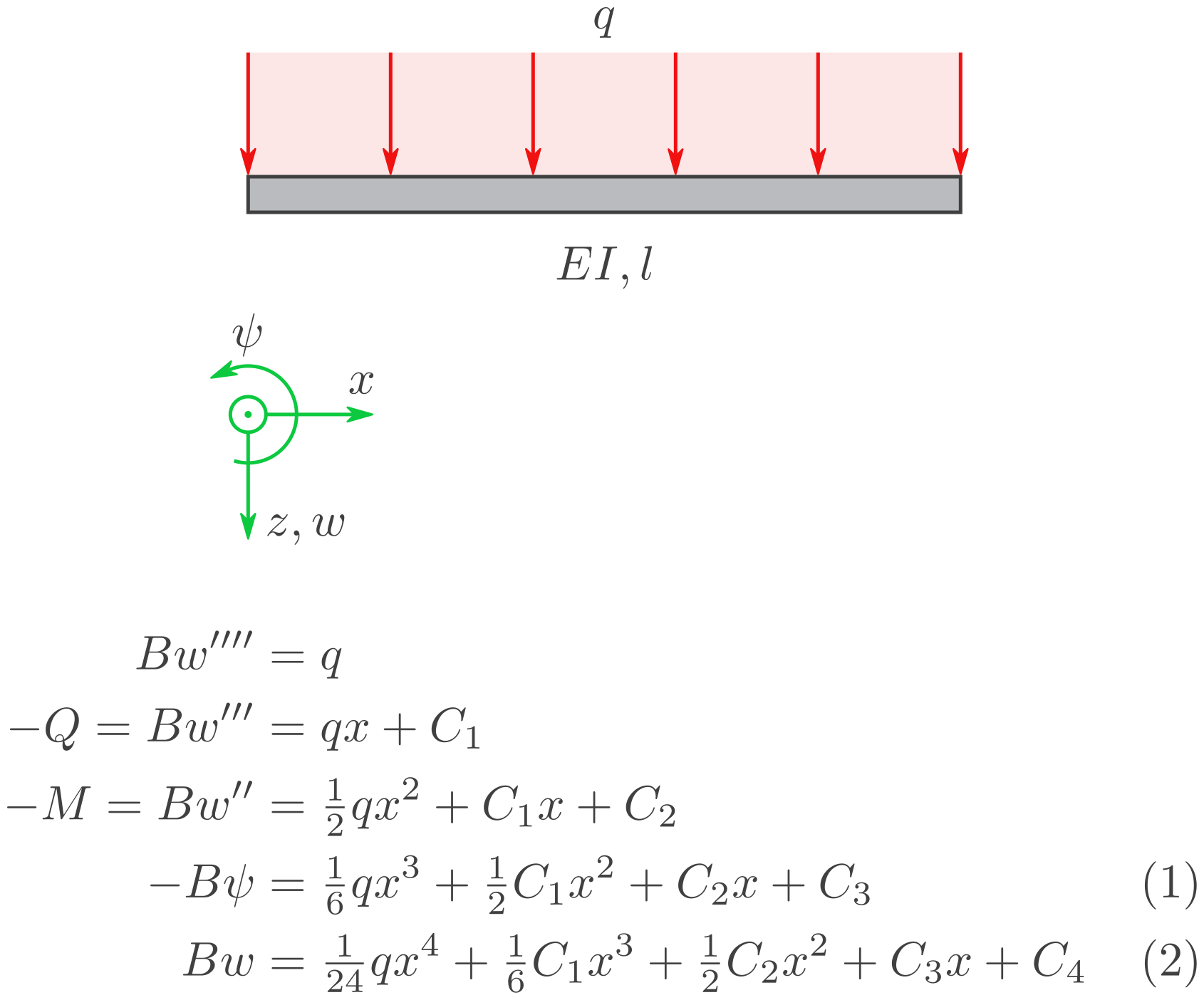
\(q\): Konstante verteilte Kraft.
\(B=EI\): Konstante Biegesteifigkeit.
Einzellasten nur an den Knoten.
\(M\) und \(Q\): Schnittgrößen.
\(w\): Querverschiebung.
\(\psi=-w'\): Neigungswinkel des Balkenquerschnitts.
Bezeichnungen
\((C_1, C_2, C_3, C_4)\): Integrationskonstanten.
\((M_1, F_1, M_2, F_2)\): Knotenlasten.
\((\psi_1, w_1, \psi_2, w_2, q)\): Freiheitsgrade.
Knotenlasten (Konstanten)
Der Zusammenhang zwischen den Knotenlasten und den Konstanten wird mit den Randbedingungen ermittelt. Dazu werden infinitesimal schmale Balkenstreifen freigeschnitten.
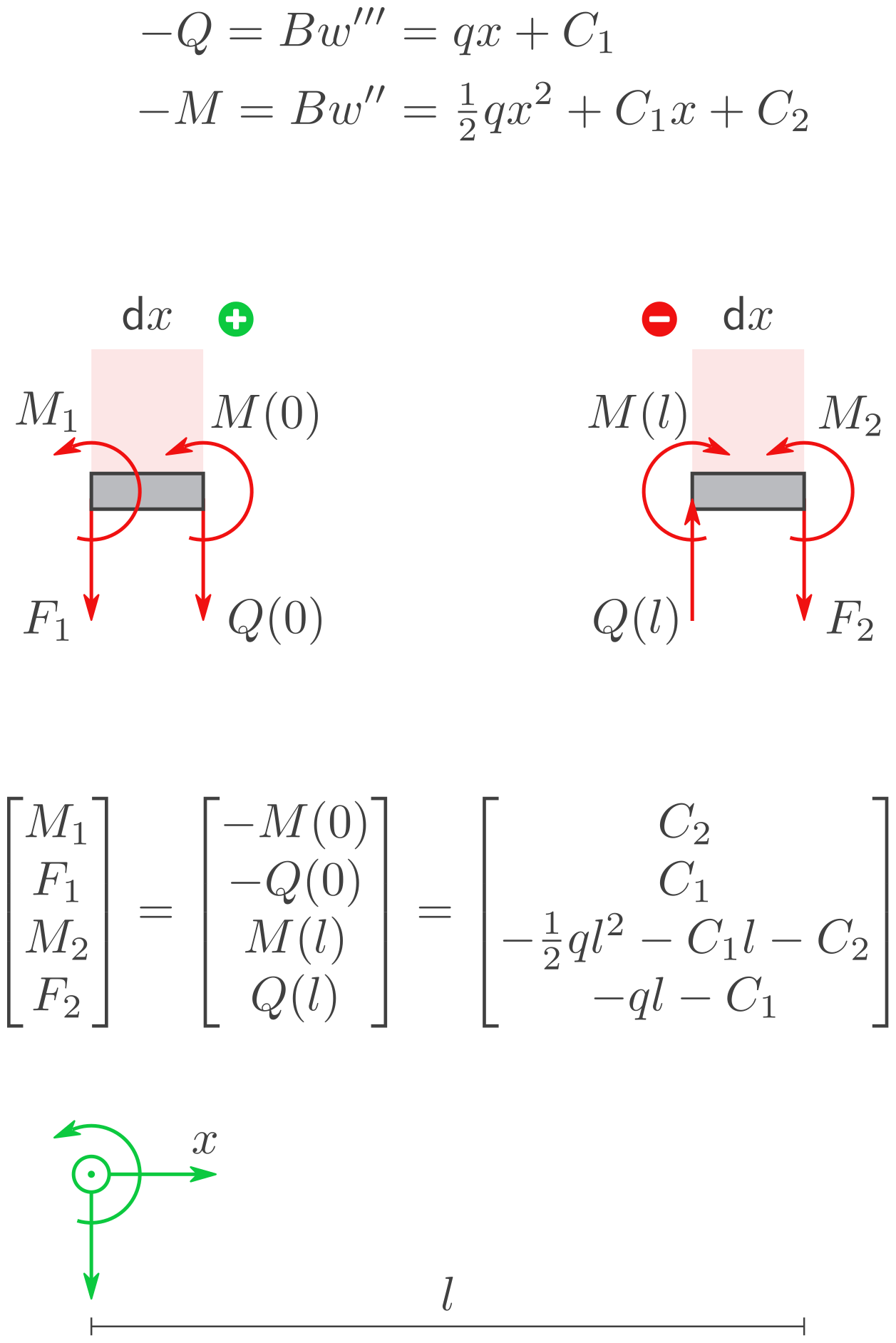
Konstanten (Freiheitsgrade)
Fünf Lastfälle werden definiert. In jedem Lastfall ist genau ein Freiheitsgrad „aktiv“. Davon abhängig ergeben sich die Integrationskonstanten abhängig von den Freiheitsgraden:
Lastfall |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
\(\psi(0)=\) |
\(\psi_1\) |
\(0\) |
\(0\) |
\(0\) |
\(0\) |
\(w(0)=\) |
\(0\) |
\(w_1\) |
\(0\) |
\(0\) |
\(0\) |
\(\psi(l)=\) |
\(0\) |
\(0\) |
\(\psi_2\) |
\(0\) |
\(0\) |
\(w(l)=\) |
\(0\) |
\(0\) |
\(0\) |
\(w_2\) |
\(0\) |
\(q=\) |
\(0\) |
\(0\) |
\(0\) |
\(0\) |
\(q\) |
\(\phantom{X}\) |
|||||
\(C_1=\) |
\(- \tfrac{6 B}{l^{2}}\) |
\(\tfrac{12 B}{l^{3}}\) |
\(- \tfrac{6 B}{l^{2}}\) |
\(- \tfrac{12 B}{l^{3}}\) |
\(-\tfrac12 l\) |
\(C_2=\) |
\(\tfrac{4 B}{l}\) |
\(- \tfrac{6 B}{l^{2}}\) |
\(\tfrac{2 B}{l}\) |
\(\tfrac{6 B}{l^{2}}\) |
\(\tfrac{1}{12}l^2\) |
\(C_3=\) |
\(- B\) |
\(0\) |
\(0\) |
\(0\) |
\(0\) |
\(C_4=\) |
\(0\) |
\(B\) |
\(0\) |
\(0\) |
\(0\) |
Lastfall 1 ist definiert über: Lastfall 2 entsprechend: Für Lastfall 1 berechnet man: Für Lastfall 2 entsprechend: Berechnung von \(C_1, C_2, C_3, C_4\) für Lastfall 1 mit: (1), (2) sind Gleichungen für \(\psi\) und \(w\). Auswerten dieser Gleichungen bei \(x=0\) und \(x=l\) liefert mit \(q(x)=0\): (a,b,c,d) eingesetzt in (1a,2b,1c,2d) liefert: Dies ist ein lineares Gleichungssystem. Und daraus lassen sich die Konstanten für den ersten Lastfall berechnen. Die Informationen aus den letzten beiden Abschnitten werden zusammengeführt: Im Abschnitt Knotenlasten (Konstanten) sind die Knotenlasten abhängig von den Konstanten dargestellt. Im Abschnitt Konstanten (Freiheitsgrade) sind die Konstanten abhängig von den Freiheitsgraden dargestellt. Hier in diesem Abschnitt sind die Knotenlasten abhängig von den Freiheitsgraden dargestellt. \(\psi_1\) \(w_1\) \(\psi_2\) \(w_2\) \(q\) \(M_1\) \(\tfrac{4 B}{l}\) \(- \tfrac{6 B}{l^{2}}\) \(\tfrac{2 B}{l}\) \(\tfrac{6 B}{l^{2}}\) \(\tfrac{1}{12} l^2\) \(F_1\) \(- \tfrac{6 B}{l^{2}}\) \(\tfrac{12 B}{l^{3}}\) \(- \tfrac{6 B}{l^{2}}\) \(- \tfrac{12 B}{l^{3}}\) \(- \tfrac12 l\) \(M_2\) \(\tfrac{2 B}{l}\) \(- \tfrac{6 B}{l^{2}}\) \(\tfrac{4 B}{l}\) \(\tfrac{6 B}{l^{2}}\) \(-\tfrac{1}{12} l^2\) \(F_2\) \(\tfrac{6 B}{l^{2}}\) \(- \tfrac{12 B}{l^{3}}\) \(\tfrac{6 B}{l^{2}}\) \(\tfrac{12 B}{l^{3}}\) \(-\tfrac12 l\) Proportionalität: Dasselbe mit Matrizen: Dieses Gleichungssystem lässt sich anschaulich interpretieren: Wenn z.B. ein bestimmter Verdrehwinkel \(\psi_1\) einstellt wird und wenn gleichzeitig die anderen Freiheitsgrade alle Null sind (\(w_1 = \psi_2 = w_2 = = 0\)): dann gilt: Wenn z.B. eine bestimmte Querverschiebung \(w_1\) einstellt wird und wenn gleichzeitig die anderen Freiheitsgrade alle Null sind (\(\psi_1 = \psi_2 = w_2 q = 0\)): dann gilt: Die Knotenlasten sind also proportional zu den Freiheitsgraden. Der Zusammenhang zwischen Freiheitsgraden und Knotenlasten ist linear. Gleichung (3) anders notiert und mit \(EI=B\) liefert: Gleichung (3) lässt sich notieren als: Oder nochmals anders notiert: Zu jedem Lastfall wurden die zugehörigen Integrationskonstanten berechnet. Einsetzen dieser Integrationskonstanten in (2) liefert die Gesamt-Querverschiebung als Überlagerung (Superposition) der Querverschiebungen der fünf Lastfälle: mit: Mit Matrix-Schreibweise notiert ist das: mit \(\xi=\tfrac x l\). Die Funktionen \(N_1\) bis \(N_5\) sind Interpolationsfunktionen. Und diese Interpolationsfunktionen werden im Postprocessing verwendet zur Berechnung der Querverschiebungen zwischen den Knoten, siehe Querverschiebung w.Details
Knotenlasten (Freiheitsgrade)
Details
Steifigkeitsmatrix und Lineares System
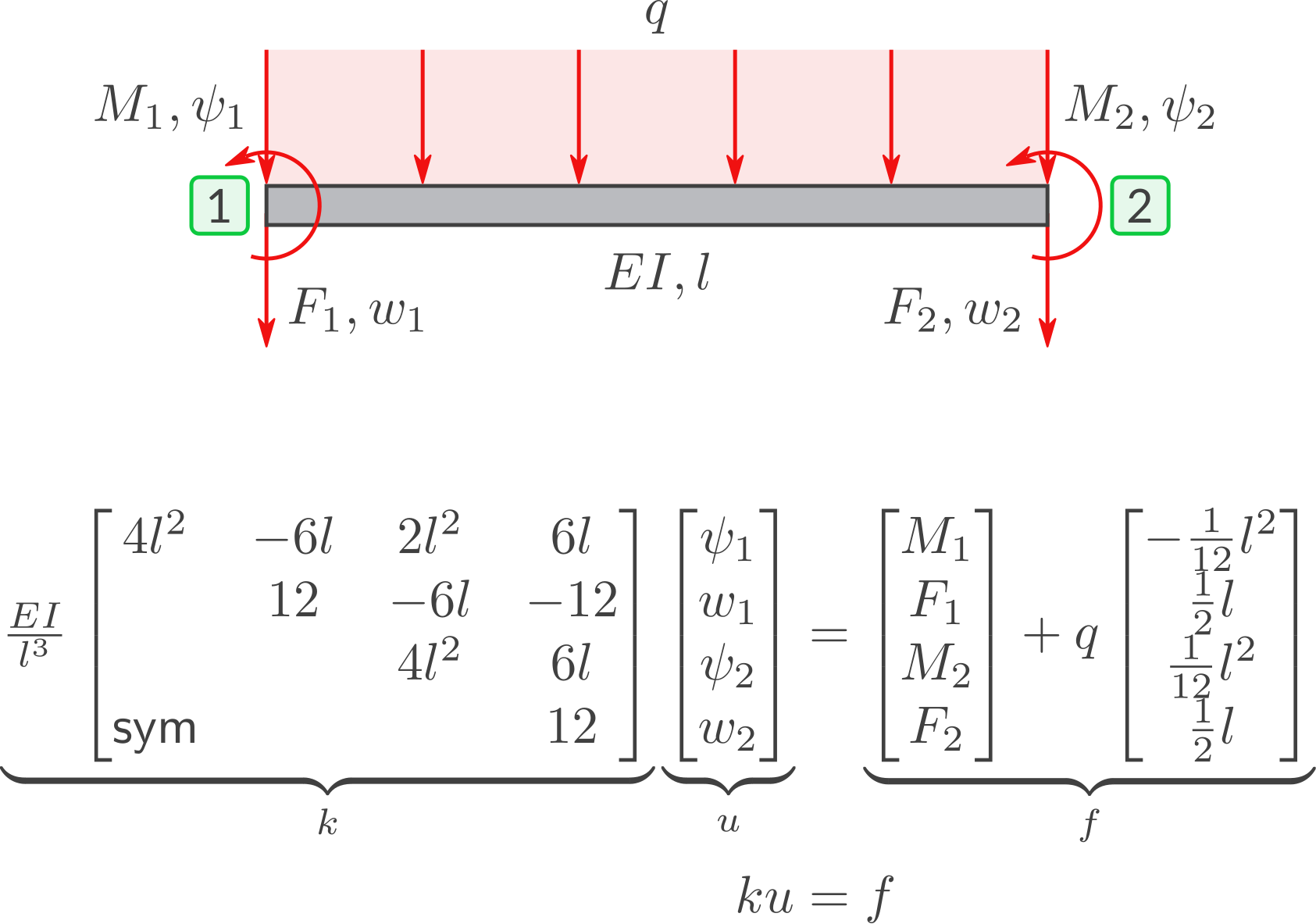
Details
Querverschiebung