B2.D
Klassische Lösung
siehe 2.4.2.I
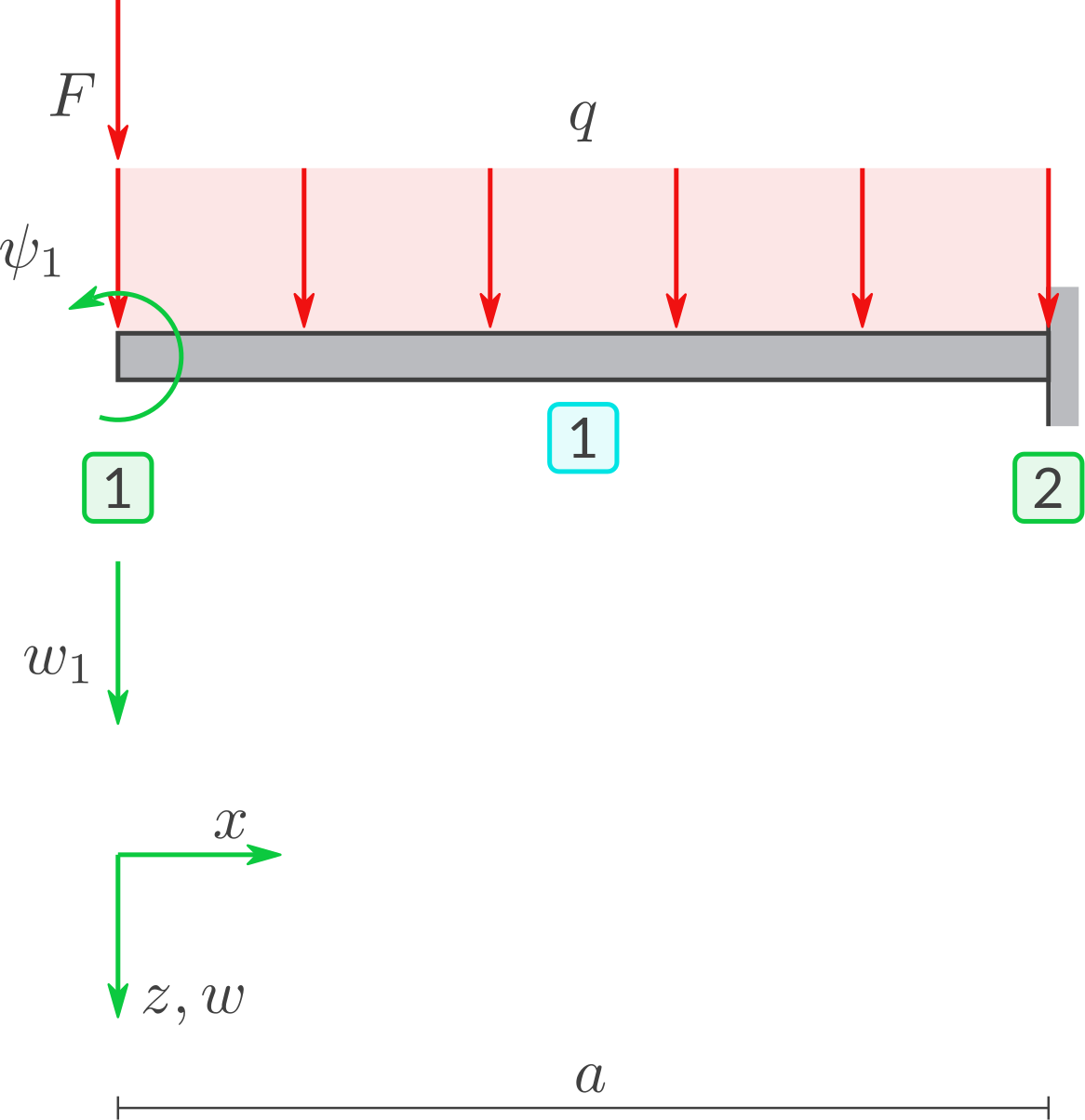
Gegebene Symbole: \(a, q, F, E, I\).
Gegeben ist ein Balken mit Elastizitätsmodul \(E\) und Flächenträgheitsmoment \(I\).
Berechnen Sie damit den Neigungswinkel \(\psi_1\) und die Querverschiebung \(w_1\). Verwenden Sie die Bezeichnungen aus Balken-Element B2. Gehen Sie wie folgt vor:
a) FEM-Gleichung
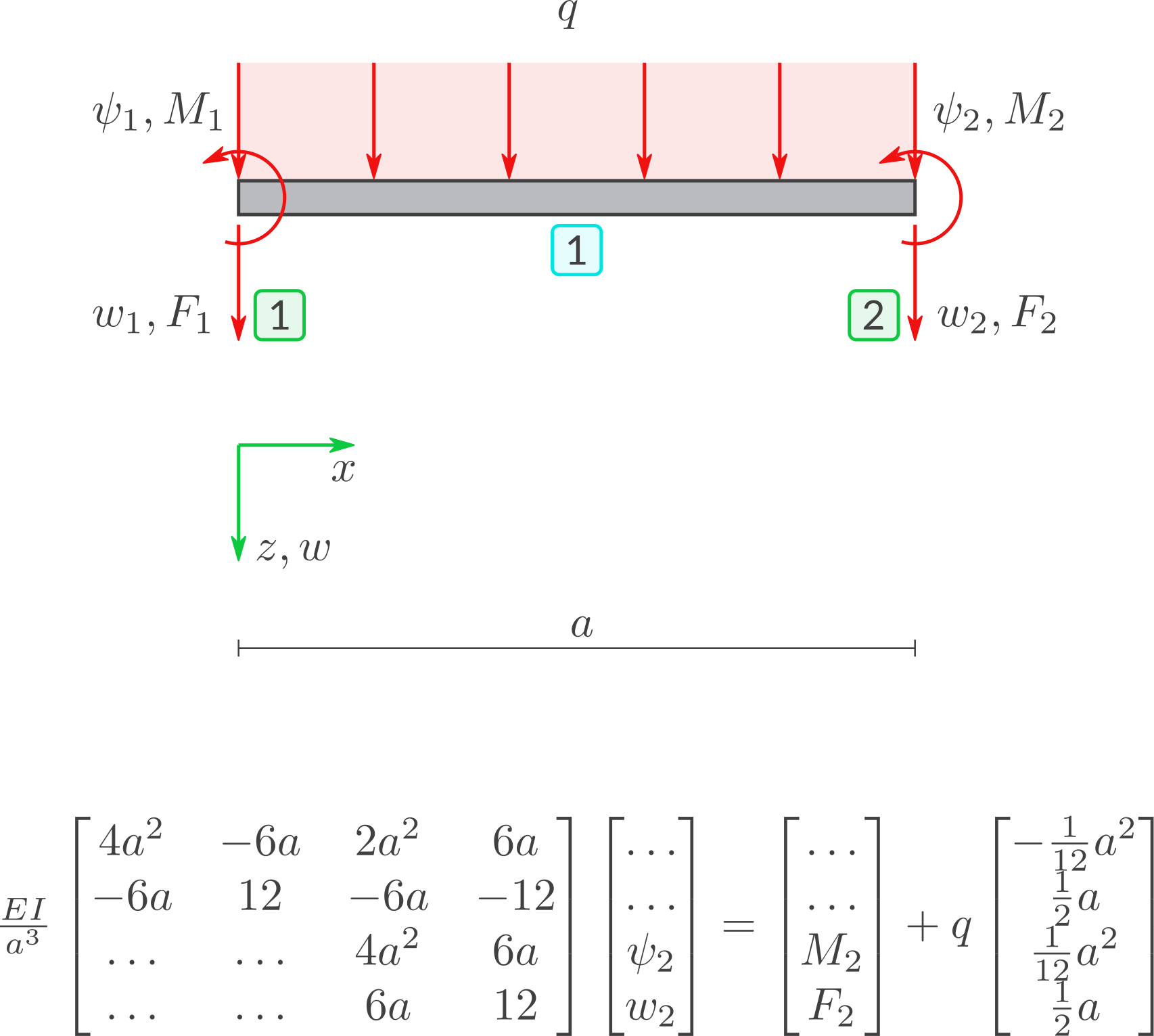
Tragen Sie die in der Gleichung fehlenden Werte ein.
Lösung
b) Superposition
Sei:
\((\psi_F, w_F)\): Neigungswinkel und Querverschiebung aufgrund \(F\) am linken Rand.
\((\psi_q, w_q)\): Neigungswinkel und Querverschiebung aufgrund \(q\) am linken Rand.
Falls beide Lasten wirken, ist:
Zeigen Sie, dass:
Einsetzen der Randbedingungen: und: in die ersten beiden Gleichungen liefert: Dazu äquivalent ist: Lösung: so dass:Lösung
c) Lösung für gegebene Größen
Seien folgenden Größen gegeben:
Berechnen Sie hierfür \(\psi_1\) in \(\mathrm{^\circ}\) (Grad) und \(w_1\) in \(\mathrm{mm}\) (Millimeter). Und zwar gerundet auf Rundestellenwert \(0{,}01\).
Oben wurde berechnet: Einsetzen der gegebenen Größen liefert:Lösung
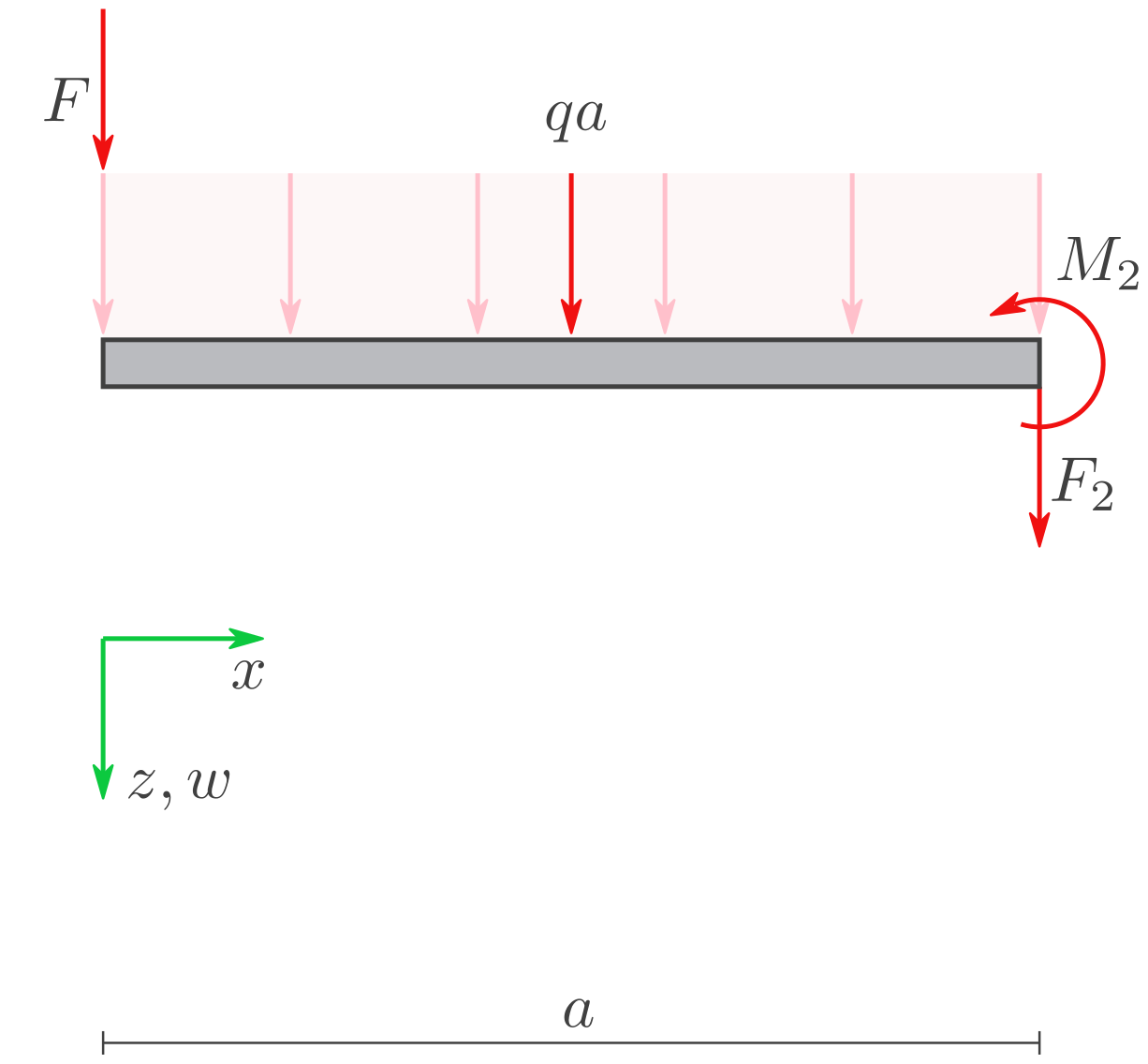
d) Lagerreaktionen
Berechnen Sie für diese Größen die Lagerreaktionen in \(\mathrm{kNm}\) (Kilonewtonmeter) bzw. \(\mathrm{kN}\) (Kilonewton):
mit der FEM-Gleichung und
unter Verwendung der Gleichgewichtsbedingungen.
\((M_2, F_2)\) sind die Lagerreaktionen. Betrachtung der letzten beiden Gleichungen der FEM-Gleichung in Matrix-Form: Berechnen von \((M_2, F_2)\) führt auf: Verwendung der Gleichgewichtsbedingungen: Also dasselbe Ergebnis wie vorher.Lösung
e) Feder
Statt der verteilten Last \(q\) sei jetzt eine Feder mit Federsteifigkeit \(c\) wirksam.

Gegebenes Symbol: \(c\). Gegebene Größe:
Berechnen Sie hierfür \(\psi_1\) und \(w_1\):
abhängig von den gegebenen Symbolen. Zeigen Sie, dass:
\[\begin{split}\psi_1 &= \frac{3 F a^{2}}{2 \left(3 EI + ca^{3}\right)} \\ w_1 &= \frac{F a^{3}}{3 EI + c a^{3}}\end{split}\]für die gegebenen Größen in \(\mathrm{^\circ}\) (Grad) bzw. in \(\mathrm{mm}\) (Millimeter) und gerundet auf Rundestellenwert \(0{,}01\). Zeigen Sie, dass:
\[\begin{split}\psi_1 &\stackrel{\small{0{,}01}}{\approx} 0{,}12 ^\circ \\ w_1 &\stackrel{\small{0{,}01}}{\approx} 4{,}09 \,\mathrm{mm}\end{split}\]
Berechnen von \(\psi_1\) und \(w_1\) aus diesem linearen Gleichungssystem liefert: Einsetzen der gegebenen Größen liefert: Bemerkung Wenn der linke Balkenrand sich um \(w_1\) absenkt, wird die Feder um \(w_1\) verkürzt. Im Innern der Feder wirkt dann eine Druckkraft \(c w_1\) bzw. gleichbedeutend eine Zugkraft \(- c w_1\). Von der Feder auf den Balken und nach oben gerichtet wirkt eine Kraft \(c w_1\).Lösung
Nachfolgend ein Programm, dass Sie ausführen können: Auf dem PC z.B. mit Anaconda. Im Browser (online) in drei Schritten: Copy: Source Code in die Zwischenablage kopieren. Paste: Source Code als Python-Notebook einfügen z.B. auf: JupyterLite oder JupyterLab oder Play: Ausführen. Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.SymPy
from sympy.physics.units import *
from sympy import *
# Units:
(mm, cm) = ( m/1000, m/100 )
kN = 10**3*newton
Pa = newton/m**2
MPa = 10**6*Pa
GPa = 10**9*Pa
deg = pi/180
half = S(1)/2
# Rounding:
import decimal
from decimal import Decimal as DX
from copy import deepcopy
def iso_round(obj, pv,
rounding=decimal.ROUND_HALF_EVEN):
import sympy
"""
Rounding acc. to DIN EN ISO 80000-1:2013-08
place value = Rundestellenwert
"""
assert pv in set([
# place value # round to:
"1", # round to integer
"0.1", # 1st digit after decimal
"0.01", # 2nd
"0.001", # 3rd
"0.0001", # 4th
"0.00001", # 5th
"0.000001", # 6th
"0.0000001", # 7th
"0.00000001", # 8th
"0.000000001", # 9th
"0.0000000001", # 10th
])
objc = deepcopy(obj)
try:
tmp = DX(str(float(objc)))
objc = tmp.quantize(DX(pv), rounding=rounding)
except:
for i in range(len(objc)):
tmp = DX(str(float(objc[i])))
objc[i] = tmp.quantize(DX(pv), rounding=rounding)
return objc
# ---
a, EI, F, q, c = var('a, EI, F, q, c')
spring = True
spring = False
sub_list = [
(a, 3 *m),
(q, 3 *kN/m),
(EI, 200 *GPa* 6500 *cm**4),
(F, 10 *kN),
(c, 1 *kN / mm),
]
a2 = a*a
a3 = a*a*a
K44 = EI/a3
K44 *= Matrix(
[
[ 4*a2 , -6*a , 2*a2 , 6*a ],
[ -6*a , 12 , -6*a , -12 ],
[ 2*a2 , -6*a , 4*a2 , 6*a ],
[ 6*a , -12 , 6*a , 12 ],
]
)
K = K44[0:2, 0:2]
p1,w1 = var("p1,w1")
M2,F2 = var("M2,F2")
u = Matrix([p1,w1])
if spring:
f = Matrix([0, F - c*w1])
else:
f = Matrix([0, F]) + q*Matrix([-a2/12, a/2])
unknowns = [p1, w1]
eq = Eq(K*u , f)
pprint(eq)
sol = solve(eq, unknowns)
p1, w1 = sol[p1], sol[w1]
pprint("\nψ₁:")
tmp = p1
pprint(tmp)
pprint("\nψ₁ / °:")
pprint(p1)
tmp = tmp.subs(sub_list)
tmp *= 180/pi
tmp = iso_round(tmp, "0.01")
pprint(tmp)
pprint("\nw₁:")
tmp = w1
pprint(tmp)
pprint("\nw₁ / mm:")
tmp = tmp.subs(sub_list)
tmp /= mm
tmp = iso_round(tmp, "0.01")
pprint(tmp)
if not spring:
K = K44[2:, 0:2]
u = Matrix([p1,w1])
f = Matrix([M2, F2]) + q*Matrix([a2/12, a/2])
unknowns = [M2, F2]
eq = Eq(K*u , f)
pprint(eq)
sol = solve(eq, unknowns)
M2, F2 = sol[M2], sol[F2]
pprint("\nM₂:")
tmp = M2
pprint(tmp)
pprint("\nM₂ / kNm:")
tmp = tmp.subs(sub_list)
tmp /= kN*m
pprint(tmp)
pprint("\nF₂:")
tmp = F2
pprint(tmp)
pprint("\nF₂ / kN:")
tmp = tmp.subs(sub_list)
tmp /= kN
pprint(tmp)
⎡ 4⋅EI⋅p₁ 6⋅EI⋅w₁ ⎤ ⎡ 2 ⎤
⎢ ─────── - ─────── ⎥ ⎢-a ⋅q ⎥
⎢ a 2 ⎥ ⎢────── ⎥
⎢ a ⎥ ⎢ 12 ⎥
⎢ ⎥ = ⎢ ⎥
⎢ 6⋅EI⋅p₁ 12⋅EI⋅w₁⎥ ⎢ a⋅q⎥
⎢- ─────── + ────────⎥ ⎢F + ───⎥
⎢ 2 3 ⎥ ⎣ 2 ⎦
⎣ a a ⎦
ψ₁:
2 3
3⋅F⋅a + a ⋅q
─────────────
6⋅EI
ψ₁ / °:
2 3
3⋅F⋅a + a ⋅q
─────────────
6⋅EI
0.26
w₁:
3 4
8⋅F⋅a + 3⋅a ⋅q
───────────────
24⋅EI
w₁ / mm:
9.26
⎡ 2 3 3 4 ⎤
⎢3⋅F⋅a + a ⋅q 8⋅F⋅a + 3⋅a ⋅q⎥ ⎡ 2 ⎤
⎢───────────── - ───────────────⎥ ⎢ a ⋅q⎥
⎢ 3⋅a 2 ⎥ ⎢M₂ + ────⎥
⎢ 4⋅a ⎥ ⎢ 12 ⎥
⎢ ⎥ = ⎢ ⎥
⎢ 2 3 3 4 ⎥ ⎢ a⋅q ⎥
⎢3⋅F⋅a + a ⋅q 8⋅F⋅a + 3⋅a ⋅q⎥ ⎢F₂ + ─── ⎥
⎢───────────── - ───────────────⎥ ⎣ 2 ⎦
⎢ 2 3 ⎥
⎣ a 2⋅a ⎦
M₂:
2
a ⋅q
-F⋅a - ────
2
M₂ / kNm:
-87/2
F₂:
-F - a⋅q
F₂ / kN:
-19
Balken-Aufgaben in SymPy gelöst
Lösung einiger Balken-Aufgaben in einem Programm hier.