a) Betrag und Winkelposition

Gegeben ist das grüne Bezugssystem und ein Vektor über seine \((x,y)\)-Komponenten.
Berechnen Sie:
den Betrag \(v\) des Vektors und
die Winkelposition \(-180^\circ < \varphi \le 180^\circ,\) des Vektors - und zwar in \(^\circ\) (Grad).
Runden Sie jeweils auf Rundestellenwert \(0{,}1\), und fassen Sie die Komponenten in einer Matrix zusammen:
\[\begin{split}\begin{bmatrix}
v \\ \varphi
\end{bmatrix}
&\stackrel{\small{0{,}1}}{\approx}
\begin{bmatrix}
\ldots \\ \ldots^\circ
\end{bmatrix}\end{split}\]
Lösung
\[\begin{split}v &= \sqrt{(-2)^2 + 3^2} \\
&\stackrel{\small{0{,}1}}{\approx} 3{,}6 \\
\varphi
&= 2 \arctan\tfrac{v_y}{v + v_x} \\
& \stackrel{\small{0{,}1}}{\approx} 123{,}7^\circ\end{split}\]
Dasselbe anders notiert, nämlich mit Zusammenfassung der Komponenten in einer Matrix:
\[\begin{split}\begin{bmatrix}
v \\ \varphi
\end{bmatrix}
&\stackrel{\small{0{,}1}}{\approx}
\begin{bmatrix}
3{,}6 \\ 123{,}7^\circ
\end{bmatrix}\end{split}\]
b) (x,y)-Komponenten
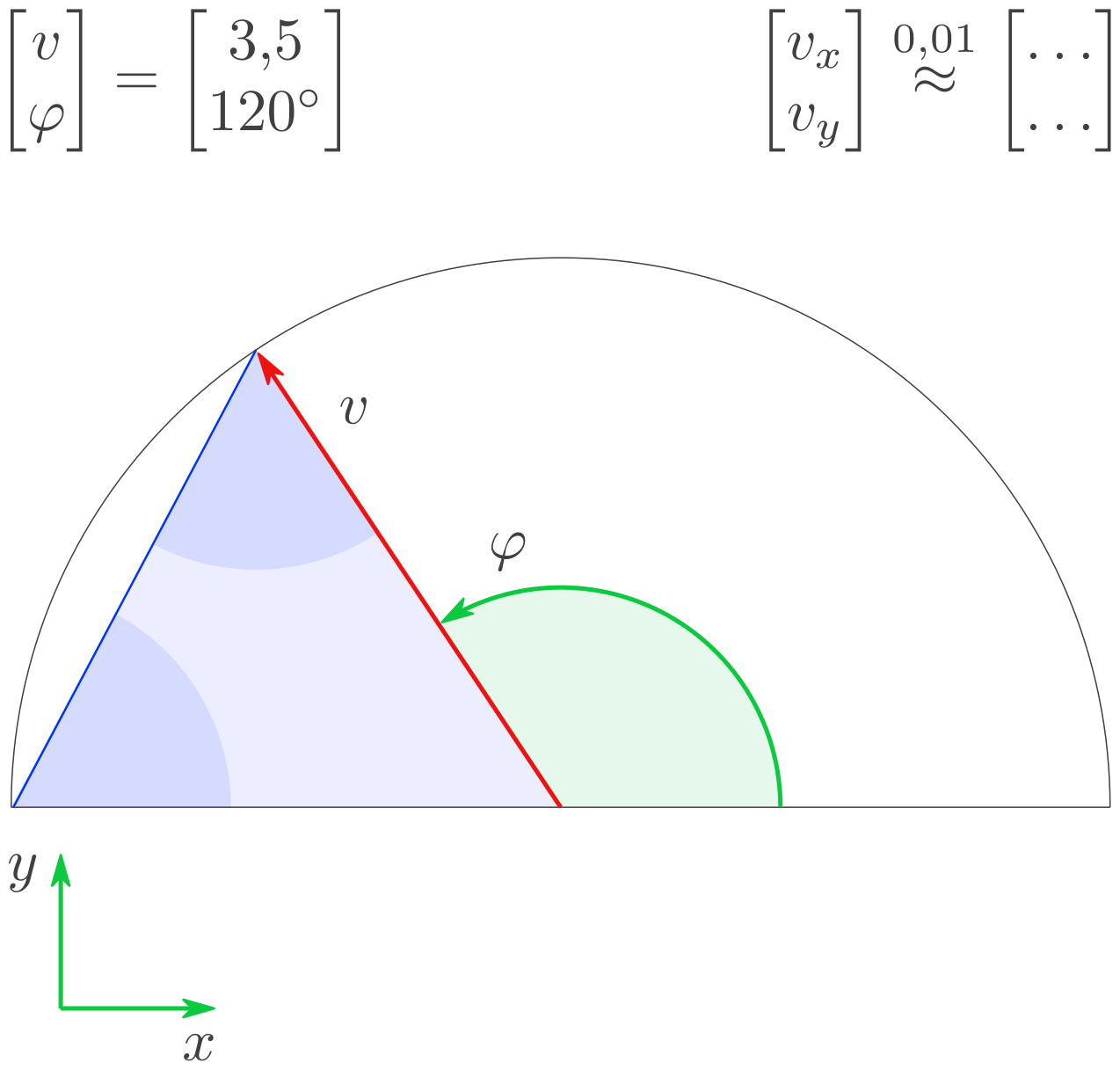
Gegeben ist das grüne Bezugssystem und ein Vektor über seine \((v,\varphi)\)-Komponenten (Polarkoordinaten).
\[\begin{split}\begin{bmatrix}
v \\ \varphi
\end{bmatrix}
=
\begin{bmatrix}
3{,}5 \\ 120^\circ
\end{bmatrix}\end{split}\]
Berechnen Sie die \((x,y)\)-Komponenten \(v_x\) und \(v_y\) - und zwar gerundet auf Rundestellenwert \(0{,}01\):
\begin{align*}
\begin{bmatrix}
v_x \\ v_y
\end{bmatrix}
&\stackrel{\small{0{,}01}}{\approx}
\begin{bmatrix}
\ldots \\
\ldots
\end{bmatrix}
\end{align*}
Lösung
\begin{align*}
\begin{bmatrix}
v_x \\ v_y
\end{bmatrix}
&=
\begin{bmatrix}
v c_\varphi \\ v s_\varphi
\end{bmatrix}
\\
&\stackrel{\small{0{,}01}}{\approx}
\begin{bmatrix}-1{,}75\\3{,}03\end{bmatrix}
\end{align*}

