2.2.C

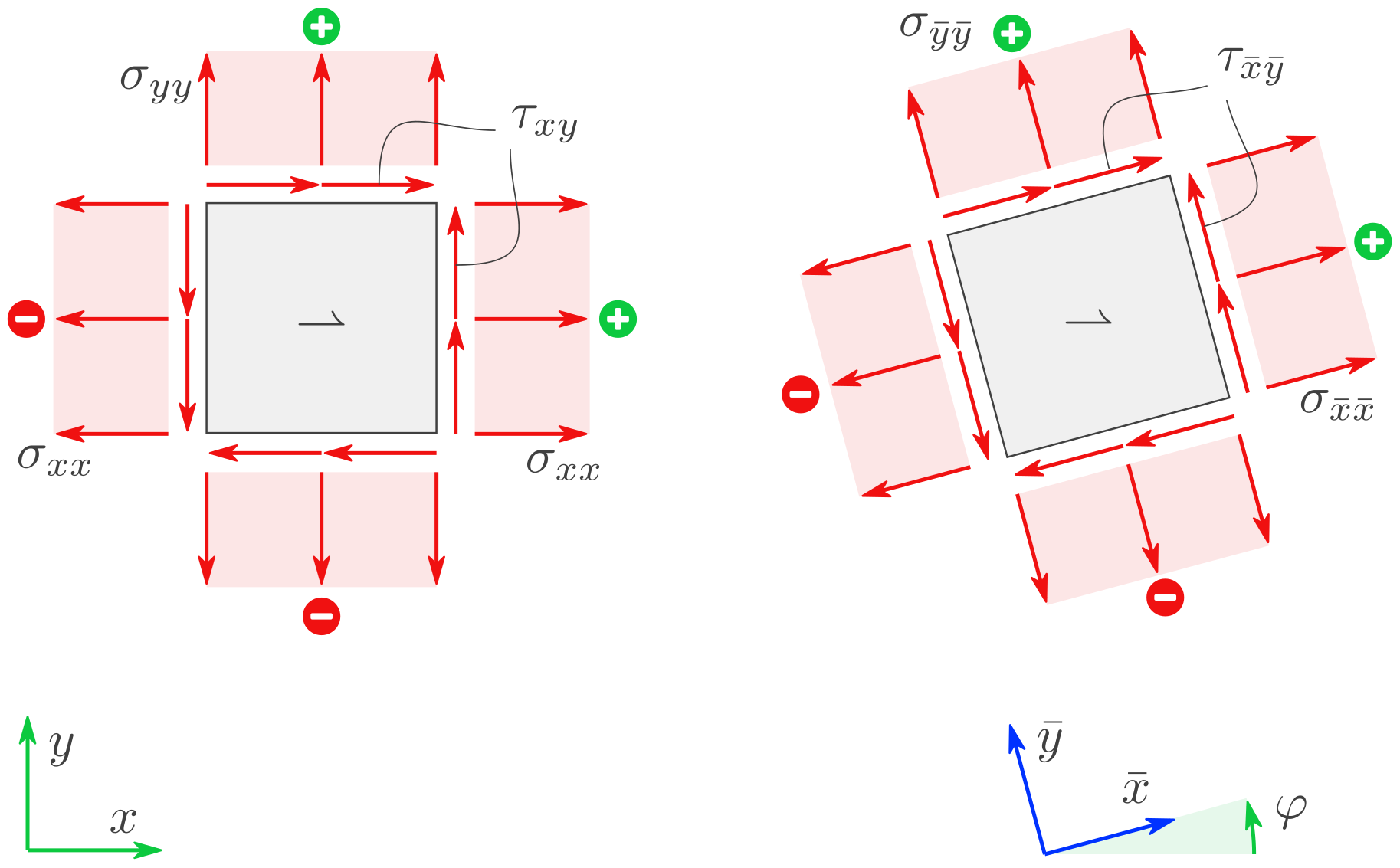
Gegebene Größen: Die \((x,y)\)-Komponenten des Spannungstensors bei einem 2D-Spannungszustand:

\[\begin{split}\begin{bmatrix} \sigma_{xx} & \tau_{xy} \\ \mathsf{sym} & \sigma_{yy} \end{bmatrix} = \begin{bmatrix} -1 & 6 \\ \mathsf{sym} & 2 \end{bmatrix} \, \mathrm{Pa}\end{split}\]

Verwenden Sie die dimensionslosen Komponenten:

\[\begin{split}\begin{bmatrix} T_{xx} & T_{xy} \\ \mathsf{sym} & T_{yy} \end{bmatrix} &= \begin{bmatrix} \frac{\sigma_{xx}}{\mathrm{Pa}} & \frac{\tau_{xy}}{\mathrm{Pa}} \\ \mathsf{sym} & \frac{\sigma_{yy}}{\mathrm{Pa}} \end{bmatrix} = \begin{bmatrix} -1 & 6 \\ \mathsf{sym} & 2 \end{bmatrix} \\ \begin{bmatrix} T_{\bar x \bar x} & T_{\bar x\bar y} \\ \mathsf{sym} & T_{\bar y\bar y} \end{bmatrix} &= \begin{bmatrix} \frac{\sigma_{\bar x\bar x}}{\mathrm{Pa}} & \frac{\tau_{\bar x\bar y}}{\mathrm{Pa}} \\ \mathsf{sym} & \frac{\sigma_{\bar y\bar y}}{\mathrm{Pa}} \end{bmatrix}\end{split}\]

Untersuchen Sie die Struktur. Gehen Sie wie folgt vor.

a) Komponenten berechnen

Berechnen Sie die dimensionslosen transformierten Komponenten gerundet auf Rundestellenwert \(0{,}01\). Zeigen Sie, dass:

• für \(\varphi = 30^\circ\):

  \[\begin{split}\begin{bmatrix} T_{\bar x \bar x} & T_{\bar x\bar y} \\ \mathsf{sym} & T_{\bar y\bar y} \end{bmatrix} \stackrel{\small{0{,}01}}{\approx} \begin{bmatrix} 4{,}95 & 4{,}3 \\ \mathsf{sym} & -3{,}95 \end{bmatrix}\end{split}\]

Lösung

Weg 1 = Mit Matrix-Multiplikation

Einsetzen der dimensionslosen Komponenten:

\[\begin{split}\begin{bmatrix} T_{xx} & T_{xy} \\ \mathsf{sym} & T_{yy} \end{bmatrix} = \begin{bmatrix} -1 & 6 \\ \mathsf{sym} & 2 \end{bmatrix}\end{split}\]

in die Transformationsformel (1) aus Passive Transformation liefert für \(\varphi = 30^\circ\):

\[\begin{split}\begin{bmatrix} T_{\bar x \bar x} & T_{\bar x\bar y} \\ \mathsf{sym} & T_{\bar y\bar y} \end{bmatrix} &= \begin{bmatrix}c_{\varphi} & s_{\varphi} \\-s_{\varphi} & c_{\varphi}\end{bmatrix} \begin{bmatrix} -1 & 6 \\ \mathsf{sym} & 2 \end{bmatrix} \begin{bmatrix}c_{\varphi} & -s_{\varphi} \\s_{\varphi} & c_{\varphi}\end{bmatrix} \\ &\! \stackrel{\small \varphi=30^\circ}{=} \begin{bmatrix}c_{ 30^\circ} & s_{ 30^\circ} \\-s_{ 30^\circ} & c_{ 30^\circ}\end{bmatrix} \begin{bmatrix} -1 & 6 \\ \mathsf{sym} & 2 \end{bmatrix} \begin{bmatrix}c_{ 30^\circ} & -s_{ 30^\circ} \\s_{ 30^\circ} & c_{ 30^\circ}\end{bmatrix} \\ &\stackrel{\small{0{,}01}}{\approx} \begin{bmatrix} 4{,}95 & 4{,}3 \\ \mathsf{sym} & -3{,}95 \end{bmatrix}\end{split}\]

Weg 2 = Ohne Matrix-Multiplikation

Statt mit Matrix-Multiplikation lassen sich die Größen auch direkt berechnen mit Gleichung (1‘) aus Passive Transformation. Verwendung der Abkürzungen:

\[\begin{split}c &= c_{2\varphi} \\ &= c_{ 60 ^\circ} \\ s &= s_{2\varphi} \\ &= s_{ 60 ^\circ}\end{split}\]

sowie:

\[\begin{split}\bar{T} &= \tfrac12 \left(T_{xx} + T_{yy}\right) \\ &\stackrel{\small{0{,}01}}{\approx} 0{,}5 \\ \tilde T &= \tfrac12 \left(T_{xx} - T_{yy}\right) \\ &\stackrel{\small{0{,}01}}{\approx} -1{,}5\end{split}\]

liefert wie oben:

\begin{align} \begin{bmatrix} T_{\bar x \bar x} & T_{\bar x\bar y} \\ \mathsf{sym} & T_{\bar y\bar y} \end{bmatrix} &= \begin{bmatrix} \bar{T} + \tilde T c + T_{xy} s & - \tilde T s + T_{xy} c\\ \mathsf{sym} & \bar{T} - \tilde T c - T_{xy} s \end{bmatrix} \\ &\stackrel{\small{0{,}01}}{\approx} \begin{bmatrix} 4{,}95 & 4{,}3 \\ \mathsf{sym} & -3{,}95 \end{bmatrix} \end{align}

b) Kreis mit Punkten zeichnen

Zeichnen Sie den Mohrschen Kreis. Markieren Sie folgende Punkte im Mohrschen Kreis:

• \(P_{0^\circ}\) bei \(\varphi=0^\circ\).

• \(P_{90^\circ}\) bei \(\varphi=90^\circ\).

• \(P_{\varphi_1}\) dort, wo \(T_{\bar x \bar x}\) maximal ist.

• \(P_{\varphi_1 \pm 90^\circ}\) dort wo \(T_{\bar x \bar x}\) minimal ist.

Lösung

c) Komponenten ablesen

Lesen Sie an Ihrem Mohrschen Kreis folgende Komponenten möglichst genau ab:

\(\varphi\)	\(T_{\bar x \bar x}\)	\(T_{\bar x \bar y}\)	\(T_{\bar y \bar y}\)
\(0 ^\circ\)
\(90 ^\circ\)
\(45 ^\circ\)
\(-45 ^\circ\)
\(180 ^\circ\)

Lösung

Berechnete Werte gerundet auf \(0{,}01\)

\(\varphi\)	\(T_{\bar x \bar x}\)	\(T_{\bar x \bar y}\)	\(T_{\bar y \bar y}\)
\(0 ^\circ\)	\(-1\)	\(6\)	\(2\)
\(90 ^\circ\)	\(2\)	\(-6\)	\(-1\)
\(45 ^\circ\)	\(6{,}5\)	\(1{,}5\)	\(-5{,}5\)
\(45 ^\circ\)	\(-5{,}5\)	\(-1{,}5\)	\(6{,}5\)
\(180 ^\circ\)	\(-1\)	\(6\)	\(2\)

d) Max. und min. Normalspannung

Zu jedem Winkel \(\varphi\) lässt sich die zugehörige Normalspannung \(T_{\bar x \bar x}(\varphi)\) berechnen. Für einige \(\varphi\) ist \(T_{\bar x \bar x}\) größer, und für andere kleiner. Ermitteln Sie die unter allen \(\varphi\) maximale und die unter allen \(\varphi\) minimale Normalspannung:

\[\begin{split}\max T_{\bar x \bar x} &\stackrel{\small{0{,}01}}{\approx} \ldots \\ \min T_{\bar x \bar x} &\stackrel{\small{0{,}01}}{\approx} \ldots\end{split}\]

Prüfen Sie Ihr Ergebnis am Mohrschen Kreis.

Berechnen Sie außerdem den zu \(\max T_{\bar x \bar x}\) gehörigen Winkel \(\varphi_1\) im Intervall \((-90^\circ, 90^\circ]\). Berechnen Sie also den Winkel, für den die Normalspannung maximal ist. Runden Sie auf Rundestellenwert \(0{,}01\). Zeigen Sie, dass:

\[\varphi_1 \stackrel{\small{0{,}01}}{\approx} 52{,}02 ^\circ\]

Lösung

\[\begin{split}\bar T &= \tfrac12 \left(T_{xx} + T_{yy}\right) \\ &\stackrel{\small{0{,}01}}{\approx} 0{,}5 \\ r &=\sqrt{\left\{ \tfrac12 \left(T_{xx}-T_{yy}\right)\right\}^2 + T_{xy}^2} \\ &\stackrel{\small{0{,}01}}{\approx} 6{,}18\end{split}\]

Damit:

\[\begin{split}\max T_{\bar x \bar x} &= \bar T + r \\ &\stackrel{\small{0{,}01}}{\approx} 6{,}68 \\ \min T_{\bar x \bar x} &= \bar T - r \\ &\stackrel{\small{0{,}01}}{\approx} -5{,}68 \\\end{split}\]

Nach A.2.4 Mohrscher Kreis gilt für den zu \(\max T_{\bar x \bar x}\) gehörigen Winkel:

\[\varphi_1 = \arctan{\tfrac{T_{xy}}{T_{xx} - \min T_{\bar x \bar x}}}\]

Laut Aufgabenstellung gilt:

• \(T_{xx} = -1\) sowie

• \(T_{xy}= 6\).

Und schon vorher verwendet wurde \(\min T_{\bar x \bar x} = \bar T - r.\) Einsetzen dieser Größen liefert:

\[\begin{split}\varphi_1 &\stackrel{\small{0{,}01}}{\approx} 52{,}02 ^\circ \\\end{split}\]

e) Max. Schubspannung

Zu jedem Winkel \(\varphi\) lässt sich die zugehörige Schubspannung \(T_{\bar x \bar y}(\varphi)\) berechnen. Für einige \(\varphi\) ist \(T_{\bar x \bar y}\) größer, und für andere kleiner. Ermitteln Sie die unter allen \(\varphi\) maximale Schubspannung:

\[\max T_{\bar x \bar y} = \ldots\]

Prüfen Sie Ihr Ergebnis am Mohrschen Kreis.

Berechnen Sie außerdem den zu \(\max T_{\bar x \bar y}\) gehörigen Winkel \(\varphi_1-45^\circ\) im Intervall \((-135^\circ, 45^\circ]\). Berechnen Sie also den Winkel, für den die Schubspannung maximal ist. Zeigen Sie, dass:

\[\varphi_1 - 45^\circ \stackrel{\small{0{,}01}}{\approx} 7{,}02 ^\circ\]

Lösung

Es gilt:

\[\begin{split}\max T_{\bar x \bar y} &= r \\ &\stackrel{\small{0{,}01}}{\approx} 6{,}18\end{split}\]

Am Mohrschen Kreis erkennt man, dass der Winkel, für den die Schubspannung maximal ist, um 45 Grad kleiner ist, als der Winkel, für den die Normalspannung maximal ist.

\[\varphi_1 - 45^\circ \stackrel{\small{0{,}01}}{\approx} 7{,}02 ^\circ\]