1.7.D
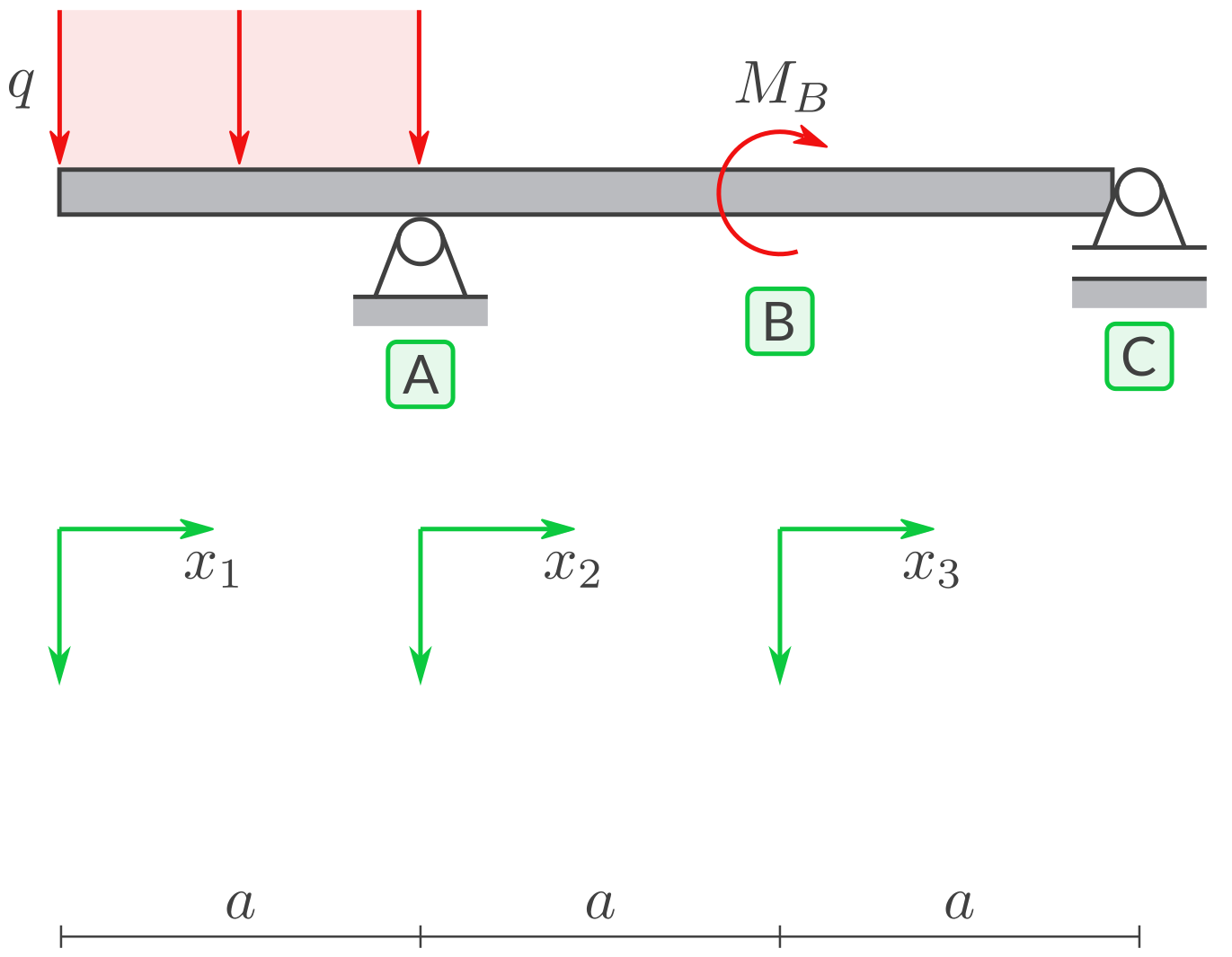
Gegebene Symbole: \(a, q\) und davon abhängig \(M_B=q a^2.\)
a) Lagerreaktionen
Für die gegebenen Symbole: Berechnen Sie die Lagerreaktionen bei A und C.
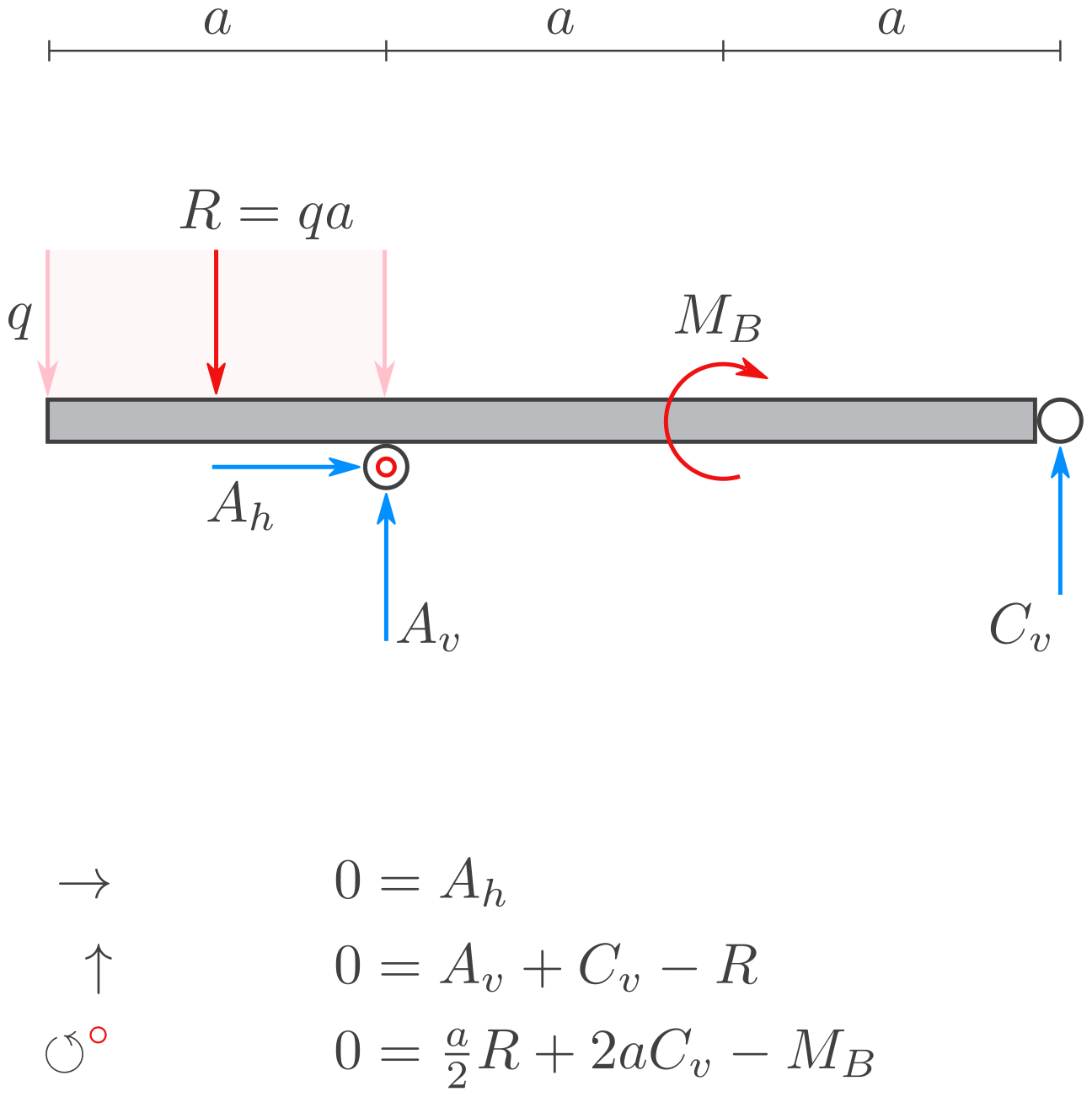
Lösung nach Einsetzen von \(M_B=q a^2\) und \(R=qa\):
Nachfolgend ein Programm, dass Sie ausführen können: Auf dem PC z.B. mit Anaconda. Im Browser (online) in drei Schritten: Copy: Source Code in die Zwischenablage kopieren. Paste: Source Code als Python-Notebook einfügen z.B. auf: JupyterLab oder Play: Ausführen. Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.
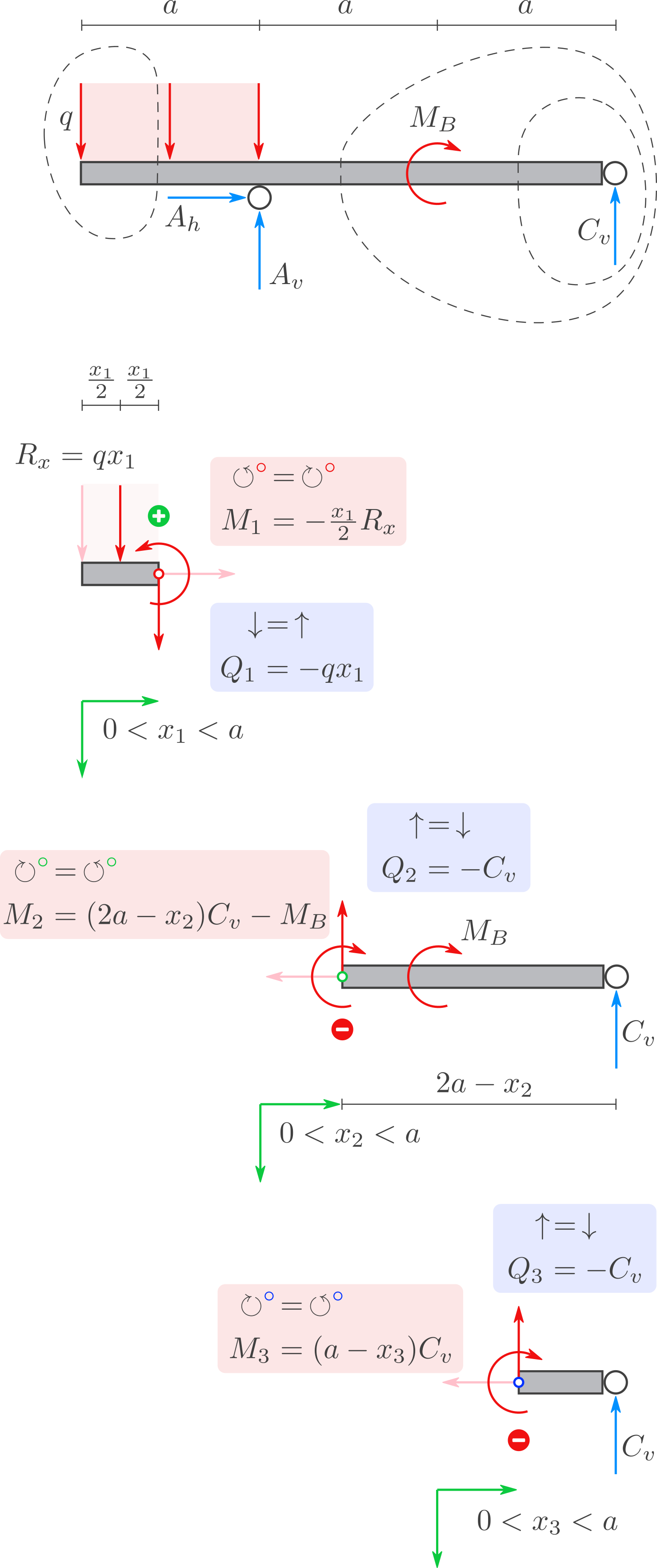
Für die gegebenen Symbole: Definieren Sie drei Definitionsbereiche: Und berechnen Sie die Schnittgrößen Querkraft und Biegemoment in den drei Bereichen: Lösung nach Einsetzen der Lagerreaktionen: mit den Abkürzungen \(\xi_1 = \tfrac{x_1}{a}, \xi_2 = \tfrac{x_2}{a}, \xi_3 = \tfrac{x_3}{a}\) und deren Definitionsbereichen:
Zeichnen Sie die Schnittgrößen Querkraft und Biegemoment in den drei Bereichen: \(\tfrac{Q_1}{qa}\) und \(\tfrac{M_1}{qa^2}\) über \(\xi_1\) \(\tfrac{Q_2}{qa}\) und \(\tfrac{M_2}{qa^2}\) über \(\xi_2\) \(\tfrac{Q_3}{qa}\) und \(\tfrac{M_3}{qa^2}\) über \(\xi_3\) mit den Abkürzungen \(\xi_1 = \tfrac{x_1}{a}, \xi_2 = \tfrac{x_2}{a}, \xi_3 = \tfrac{x_3}{a}\).
Berechnen Sie: die Kraft, die vom Lager bei C auf den Balken wirkt und die Querkraft und das Biegemoment sehr nah bei C für die Größen:
Berechnen Sie die Schnittgrößen in den ersten beiden Bereichen mit den Biege-Differentialgleichungen:
Lösung
SymPy
from sympy.physics.units import *
from sympy import *
a, q = var("a, q")
# Given:
M = q*a*a
R = q*a
Ah, Av, Cv = var('A_h, A_v, C_v')
# Equil. Conditions:
eq1 = Eq( 0, Ah )
eq2 = Eq( 0, Av + Cv - R )
eq3 = Eq( 0, a/2 * R + 2*a*Cv - M)
# Solve:
eqns = [eq1, eq2, eq3]
sol = solve(eqns, [Ah, Av, Cv])
# Output:
for s in sol:
pprint("\n")
pprint(s)
tmp = sol[s]
pprint(tmp)
Aₕ
0
Aᵥ
3⋅a⋅q
─────
4
Cᵥ
a⋅q
───
4
b) Querkraft und Biegemoment
Lösung
c) Funktionsgraphen
Lösung
d) Lagerkraft und Schnittgrößen bei C
Lösung
e) Differentialgleichungen
Lösung