3.4.C

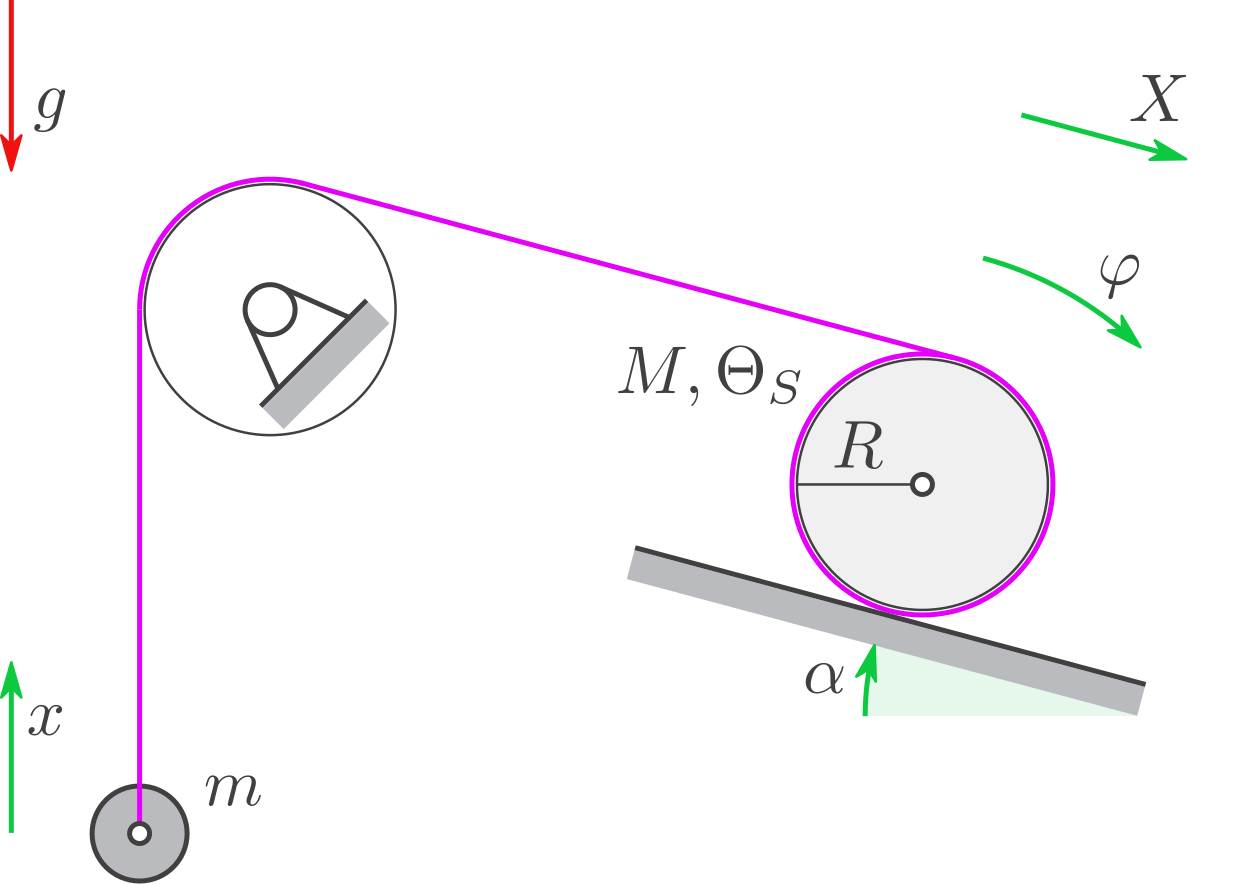
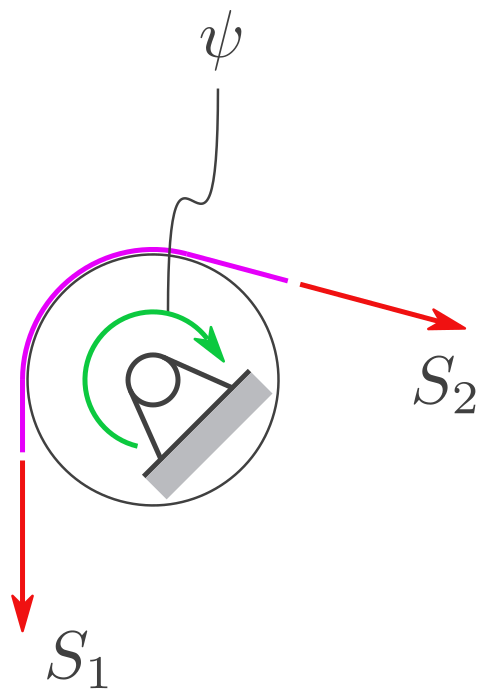
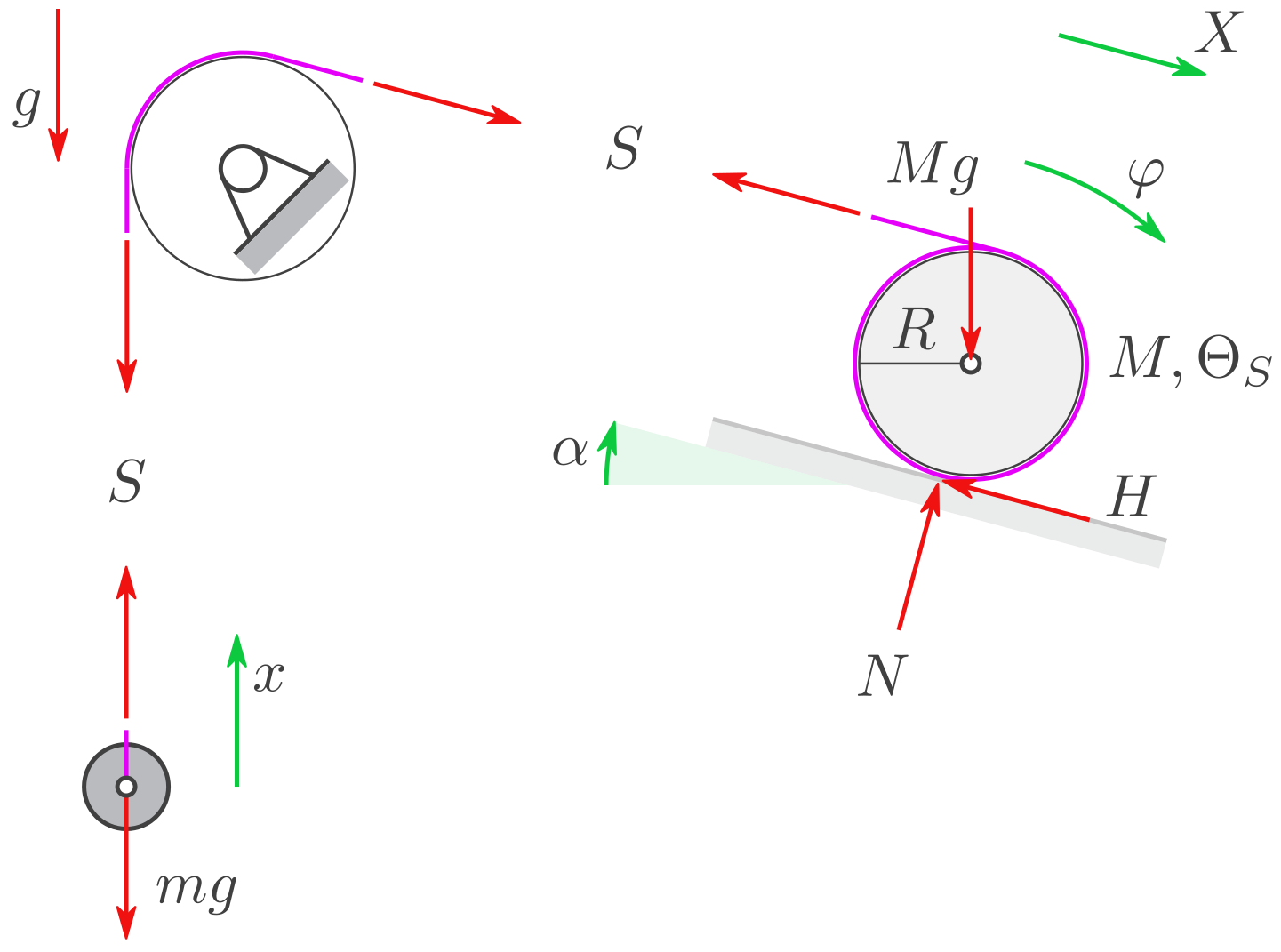
../../../_images/3.4.C.png — Geg. *Symbole*: \(g, M, m, R, \alpha\) und davon abhängig das Massenträgheitsmoment der Scheibe bezogen auf ihren Schwerpunkt: \(\Theta_S=\tfrac12 M R^2.\)

Eine Scheibe mit Masse \(M\) rollt nach unten und wickelt dabei ein Seil auf.
Das über die masselose Umlenkrolle gelegte Seil zieht eine Punktmasse mit Masse \(m\) nach oben.

Berechnen Sie die Beschleunigung \(\ddot X\) des Schwerpunkts der Scheibe.

Gehen Sie wie folgt vor:

a) Seilkraft

Zeigen Sie, dass die Seilkraft zwischen der Punktmasse und der masselosen Umlenkrolle genauso groß ist wie die Seilkraft zwischen der Umlenkrolle und der Scheibe.

Lösung

Das Massenträgheitsmoment der Rolle ist Null, weil die Rolle keine Masse hat. Der Drallsatz lautet - angenommen, die Rolle hätte den Radius \(r\):

\[0 \cdot \ddot \psi = r S_2 - r S_1\]

Und darum ist die Seilkraft überall gleich groß, nämlich:

\[S_1 = S_2 =: S\]

b) Schwerpunktsatz & Drallsatz

Schneiden Sie Punktmasse und Scheibe frei. Geben Sie an:

Schwerpunktsatz in \(x\)-Richtung für die Punktmasse,
Schwerpunktsatz in \(X\)-Richtung für die Scheibe und
Drallsatz um den Schwerpunkt der Scheibe.

Lösung

\[\begin{split}m \ddot x &= -m g + S \\ M \ddot X &= M g \sin\alpha - S - H\\ \Theta_S \ddot \varphi &= R ( H - S)\end{split}\]

c) Kinematik

Geben Sie die die Zwangsbedingungen an:

zwischen \(\ddot X\) und \(\ddot\varphi\) und
zwischen \(\ddot x\) und \(\ddot\varphi\).

Lösung

\[\begin{split}\ddot X &= R \ddot \varphi \\ \ddot x &= 2 R \ddot \varphi\end{split}\]

Details

Die Scheibe ist ein Rad, welches mit Winkelgeschwindigkeit \(\dot\varphi\) rollt.
Ein Teilchen auf dem (Massen-)Mittelpunkt des Rads bewegt sich nach rechts unten (parallel zum Boden) mit \(\dot X = R\dot\varphi\).
Alle Teilchen auf dem oberen Seilstück bewegen sich nach rechts unten (parallel zum Boden) mit: \(\dot x = 2R\dot\varphi\).
Alle Teilchen auf dem Seilstück links bewegen sich nach oben mit: derselben Geschwindigkeit \(\dot x = 2R\dot\varphi\).

d) Lösung

Die oben genannten Aussagen bilden ein Gleichungssystem bestehend aus 5 Gleichungen.
In diesen Gleichungen gibt es die 5 Unbekannten: Haftkraft, Seilkraft und \(\ddot x, \ddot X, \ddot \varphi\).
Die Lösung des Gleichungssystems liefert unter Anderem:

\[\begin{split}\ddot x &= \tfrac{4 g \left(M \sin {\alpha} - 2 m\right)}{3 M + 8 m} \\ \ddot X &= \tfrac{2 g \left(M \sin {\alpha} - 2 m\right)}{3 M + 8 m} \\ \ddot \varphi &= \tfrac{2 g \left(M \sin {\alpha} - 2 m\right)}{R \left(3 M + 8 m\right)}\end{split}\]

Zeigen Sie, dass diese Ausdrücke für \(\ddot x, \ddot X\) und \(\ddot \varphi\) die kinematischen Beziehungen erfüllen.

Lösung

Einsetzen liefert:

\[\begin{split}\ddot x &= 2 R \ddot \varphi \\ \tfrac{4 g \left(M \sin {\alpha} - 2 m\right)}{3 M + 8 m} &= 2 R \tfrac{2 g \left(M \sin {\alpha} - 2 m\right)}{R \left(3 M + 8 m\right)}\\ 1&=1\end{split}\]

und:

\[\begin{split}\ddot X &= R \ddot \varphi \\ \tfrac{2 g \left(M \sin {\alpha} - 2 m\right)}{3 M + 8 m} &= R \tfrac{2 g \left(M \sin {\alpha} - 2 m\right)}{R \left(3 M + 8 m\right)}\\ 1&=1\end{split}\]

e) \(\ddot X\) für geg. Größen

Verwenden Sie erst ab hier folgende Größen:

\[\begin{split}g &= 10\, \tfrac{\mathrm{m}}{{\mathrm{s}}^2} \\ M &=4 \,\mathrm{kg} \\ m &= 0{,}5 \,\mathrm{kg} \\ R &= 0{,}1 \, \mathrm{m} \\ \alpha &= 30^\circ\end{split}\]

Zeigen Sie, dass gilt:

\[\ddot X = 1{,}25 \, \tfrac{\mathrm{m}}{{\mathrm{s}}^2}\]

Lösung

\[\begin{split}\ddot X &= 20 \, \tfrac{\mathrm{m}}{{\mathrm{s}}^2} \tfrac{\left(4 \cdot \tfrac12 - 1\right)}{12 + 4} \\ &= \tfrac 5 4 \, \tfrac{\mathrm{m}}{{\mathrm{s}}^2}\end{split}\]

f) Verstrichene Zeit

Sei die Anfangsgeschwindigkeit der Scheibe gleich Null, also \(\dot X(t=0\,\mathrm{s})=0\). Berechnen Sie die Zeit \(\Delta t\), die verstreicht, bis für die Scheiben-Geschwindigkeit gilt: \(\dot X = 1{,}25\,\tfrac{\mathrm{m}}{\mathrm{s}}.\)

Lösung

Die verstrichene Zeit ist \(\Delta t=1\,\mathrm{s}\), denn:

\[\begin{split}\dot X &= \ddot X \Delta t \\ \tfrac 5 4 \, \tfrac{\mathrm{m}}{{\mathrm{s}}} &= \tfrac 5 4 \, \tfrac{\mathrm{m}}{{\mathrm{s}}^2} \,\Delta t \\ 1 &= \tfrac{\Delta t}{\mathrm{s}} \\ \Delta t &= 1 \, \mathrm{s}\end{split}\]

SymPy

Nachfolgend ein Programm, dass Sie ausführen können:

Auf dem PC z.B. mit Anaconda.
Im Browser (online) in drei Schritten:
1. Copy: Source Code in die Zwischenablage kopieren.
2. Paste: Source Code als Python-Notebook einfügen z.B. auf:
  - JupyterLite oder
  - JupyterLab oder
  - Colab.
3. Play: Ausführen.

from sympy import *
from sympy.physics.units import kg, m, s

deg = pi/180
half = S(1)/2

R, Mass, mass, alpha= var("R, M, m, alpha")
grav = var("g")

sub_list=[
    ( Mass,          4     *kg ),
    ( mass,       half     *kg ),
    ( R,       S(1)/10      *m ),
    ( alpha,        30    *deg ),
    ( grav,         10 *m/s**2 ),
    ]

Tht=Mass*R*R/2

# Unknowns:
# A = X''
# a = x''
# ap = phi''
A, a, ap, H, S = var('A, a, ap, H, S')

eq1 = Eq( Mass*A, Mass*grav*sin(alpha)-S-H )
eq2 = Eq( Tht*ap, R*(H-S) )
eq3 = Eq( mass*a, -mass*grav+S )
eq4 = Eq( A, R*ap )
eq5 = Eq( a, 2*R*ap )

eqns = [eq1, eq2, eq3, eq4, eq5]
unks = [A, a, ap, H, S]
sol = solve(eqns, unks)
pprint(sol)

⎧                             2                                                                                                      
⎪   2⋅M⋅g⋅sin(α) - 4⋅g⋅m     M ⋅g⋅sin(α) + 4⋅M⋅g⋅m⋅sin(α) + M⋅g⋅m     4⋅M⋅g⋅m⋅sin(α) + 3⋅M⋅g⋅m     4⋅M⋅g⋅sin(α) - 8⋅g⋅m      2⋅M⋅g⋅si
⎨A: ────────────────────, H: ────────────────────────────────────, S: ────────────────────────, a: ────────────────────, ap: ────────
⎪        3⋅M + 8⋅m                        3⋅M + 8⋅m                          3⋅M + 8⋅m                  3⋅M + 8⋅m               3⋅M⋅R
⎩                                                                                                                                    

            ⎫
n(α) - 4⋅g⋅m⎪
────────────⎬
 + 8⋅R⋅m    ⎪
            ⎭

Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.