2.2.C

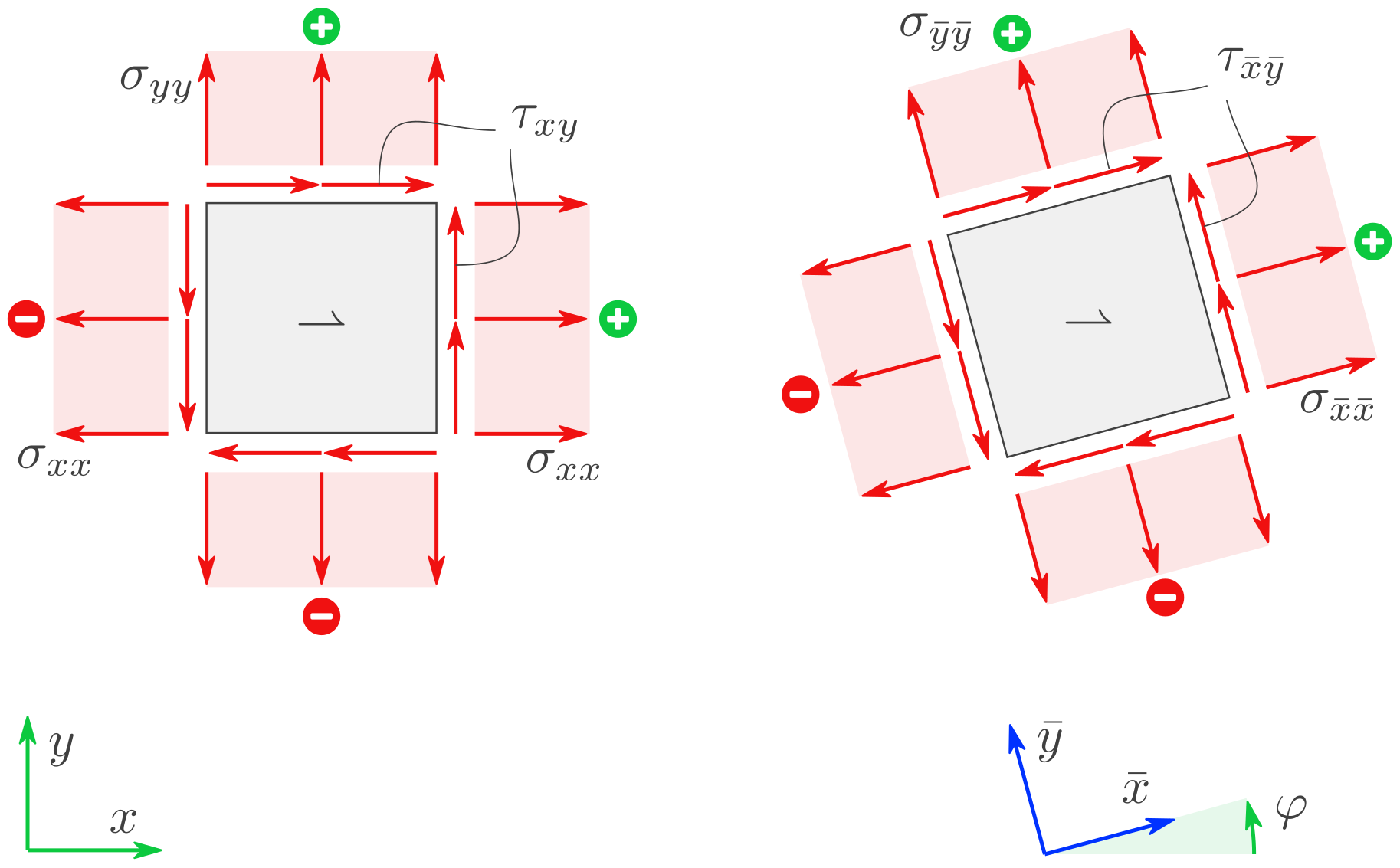
../../../_images/2.2.C.png — Gegebene *Größen*: Die \((x,y)\)-Komponenten des Spannungstensors bei einem 2D-Spannungszustand:

\[\begin{split}\begin{bmatrix} \sigma_{xx} & \tau_{xy} \\ \mathsf{sym} & \sigma_{yy} \end{bmatrix} = \begin{bmatrix} -1 & 4 \\ \mathsf{sym} & 5 \end{bmatrix} \, \mathrm{Pa}\end{split}\]

Verwenden Sie die dimensionslosen Komponenten:

\[\begin{split}\begin{bmatrix} T_{xx} & T_{xy} \\ \mathsf{sym} & T_{yy} \end{bmatrix} &= \begin{bmatrix} \frac{\sigma_{xx}}{\mathrm{Pa}} & \frac{\tau_{xy}}{\mathrm{Pa}} \\ \mathsf{sym} & \frac{\sigma_{yy}}{\mathrm{Pa}} \end{bmatrix} = \begin{bmatrix} -1 & 4 \\ \mathsf{sym} & 5 \end{bmatrix} \\ \begin{bmatrix} T_{\bar x \bar x} & T_{\bar x\bar y} \\ \mathsf{sym} & T_{\bar y\bar y} \end{bmatrix} &= \begin{bmatrix} \frac{\sigma_{\bar x\bar x}}{\mathrm{Pa}} & \frac{\tau_{\bar x\bar y}}{\mathrm{Pa}} \\ \mathsf{sym} & \frac{\sigma_{\bar y\bar y}}{\mathrm{Pa}} \end{bmatrix}\end{split}\]

und die Passive Transformation von Tensor-Komponenten.

Untersuchen Sie die Struktur. Gehen Sie wie folgt vor.

a) Komponenten berechnen

Berechnen Sie die dimensionslosen transformierten Komponenten gerundet auf Rundestellenwert \(0{,}01\). Zeigen Sie, dass:

für \(\varphi = 15^\circ\):

\[\begin{split}\begin{bmatrix} T_{\bar x \bar x} & T_{\bar x\bar y} \\ \mathsf{sym} & T_{\bar y\bar y} \end{bmatrix} \stackrel{\small{0{,}01}}{\approx} \begin{bmatrix} 1{,}4 & 4{,}96 \\ \mathsf{sym} & 2{,}6 \end{bmatrix}\end{split}\]

Lösung

Weg 1 = Mit Matrix-Multiplikation

Einsetzen der dimensionslosen Komponenten:

\[\begin{split}\begin{bmatrix} T_{xx} & T_{xy} \\ \mathsf{sym} & T_{yy} \end{bmatrix} = \begin{bmatrix} -1 & 4 \\ \mathsf{sym} & 5 \end{bmatrix}\end{split}\]

in die Transformationsformel (1) aus Passive Transformation liefert für \(\varphi = 15^\circ\):

\[\begin{split}\begin{bmatrix} T_{\bar x \bar x} & T_{\bar x\bar y} \\ \mathsf{sym} & T_{\bar y\bar y} \end{bmatrix} &= \begin{bmatrix}c_{\varphi} & s_{\varphi} \\-s_{\varphi} & c_{\varphi}\end{bmatrix} \begin{bmatrix} -1 & 4 \\ \mathsf{sym} & 5 \end{bmatrix} \begin{bmatrix}c_{\varphi} & -s_{\varphi} \\s_{\varphi} & c_{\varphi}\end{bmatrix} \\ &\! \stackrel{\small \varphi=15^\circ}{=} \begin{bmatrix}c_{15^\circ} & s_{15^\circ} \\-s_{15^\circ} & c_{15^\circ}\end{bmatrix} \begin{bmatrix} -1 & 4 \\ \mathsf{sym} & 5 \end{bmatrix} \begin{bmatrix}c_{15^\circ} & -s_{15^\circ} \\s_{15^\circ} & c_{15^\circ}\end{bmatrix} \\ &\stackrel{\small{0{,}01}}{\approx} \begin{bmatrix} 1{,}4 & 4{,}96 \\ \mathsf{sym} & 2{,}6 \end{bmatrix}\end{split}\]

Weg 2 = Ohne Matrix-Multiplikation

Statt mit Matrix-Multiplikation lassen sich die Größen auch direkt berechnen mit Gleichung (1‘) aus Passive Transformation. Verwendung der Abkürzungen:

\[\begin{split}\bar{T} &= \tfrac12 \left(T_{xx} + T_{yy}\right) \qquad & \qquad c &= c_{2\varphi} \\ \tilde T &= \tfrac12 \left(T_{xx} - T_{yy}\right) \qquad & \qquad s &= s_{2\varphi}\end{split}\]

und Einsetzen von \(\varphi = 15^\circ\) liefert wie oben:

\begin{align} \begin{bmatrix} T_{\bar x \bar x} & T_{\bar x\bar y} \\ \mathsf{sym} & T_{\bar y\bar y} \end{bmatrix} &= \begin{bmatrix} \bar{T} + \tilde T c + T_{xy} s & - \tilde T s + T_{xy} c\\ \mathsf{sym} & \bar{T} - \tilde T c - T_{xy} s \end{bmatrix} \\ &\stackrel{\small{0{,}01}}{\approx} \begin{bmatrix} 1{,}4 & 4{,}96 \\ \mathsf{sym} & 2{,}6 \end{bmatrix} \end{align}

Einsetzen von \(\varphi = 30^\circ\) statt \(\varphi = 15^\circ\) liefert wie oben:

\[\begin{split}\begin{bmatrix} T_{\bar x \bar x} & T_{\bar x\bar y} \\ \mathsf{sym} & T_{\bar y\bar y} \end{bmatrix} \stackrel{\small{0{,}01}}{\approx} \begin{bmatrix} 3{,}96 & 4{,}6 \\ \mathsf{sym} & 0{,}04 \end{bmatrix}\end{split}\]

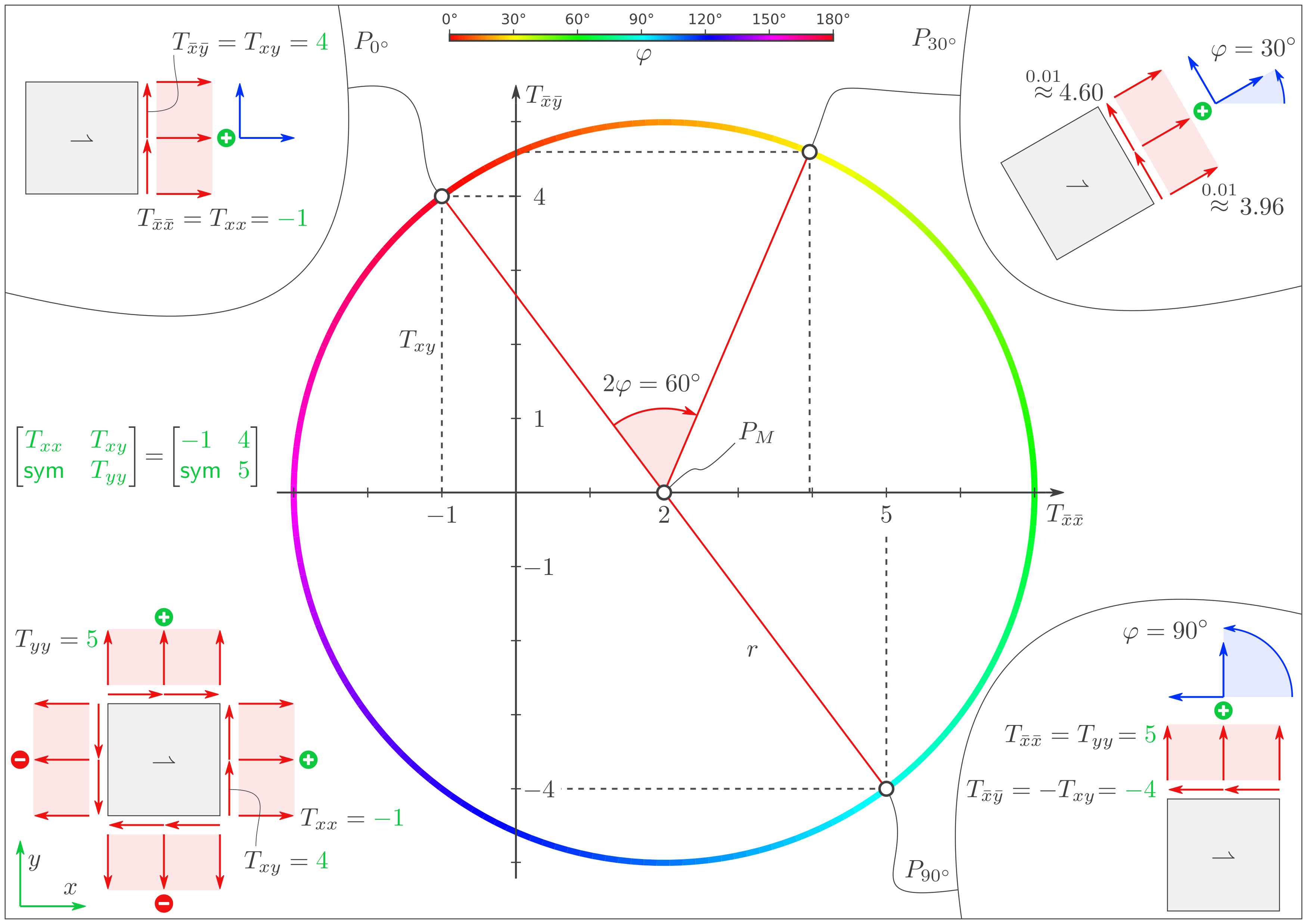
b) Kreis mit Punkten zeichnen

Zeichnen Sie den Mohrschen Kreis. Markieren Sie folgende Punkte im Mohrschen Kreis:

\(P_{0^\circ}\) bei \(\varphi=0^\circ\).
\(P_{90^\circ}\) bei \(\varphi=90^\circ\).
\(P_{\varphi_1}\) dort, wo \(T_{\bar x \bar x}\) maximal ist.
\(P_{\varphi_1 \pm 90^\circ}\) dort wo \(T_{\bar x \bar x}\) minimal ist.

Lösung

Tensor Transformation

c) Komponenten ablesen

Lesen Sie an Ihrem Mohrschen Kreis folgende Komponenten möglichst genau ab:

\(\varphi\)	\(T_{\bar x \bar x}\)	\(T_{\bar x \bar y}\)	\(T_{\bar y \bar y}\)
\(0^\circ\)
\(90^\circ\)
\(45^\circ\)
\(-45^\circ\)
\(180^\circ\)

Lösung

Ablesen liefert:

\(\varphi\)	\(T_{\bar x \bar x}\)	\(T_{\bar x \bar y}\)	\(T_{\bar y \bar y}\)
\(0 ^\circ\)	\(-1\)	\(4\)	\(5\)
\(90 ^\circ\)	\(5\)	\(-4\)	\(-1\)
\(45 ^\circ\)	\(6\)	\(3\)	\(-2\)
\(-45 ^\circ\)	\(-2\)	\(-3\)	\(6\)
\(180 ^\circ\)	\(-1\)	\(4\)	\(5\)

d) Max. und min. Normalspannung

Zu jedem Winkel \(\varphi\) lässt sich die zugehörige Normalspannung \(T_{\bar x \bar x}(\varphi)\) berechnen. Für einige \(\varphi\) ist \(T_{\bar x \bar x}\) größer, und für andere kleiner. Ermitteln Sie die unter allen \(\varphi\) maximale und die minimale Normalspannung:

\[\begin{split}\max T_{\bar x \bar x} &= \ldots \\ \min T_{\bar x \bar x} &= \ldots\end{split}\]

Prüfen Sie Ihr Ergebnis am Mohrschen Kreis.

Berechnen Sie außerdem den zu \(\max T_{\bar x \bar x}\) gehörigen Winkel \(\varphi_1\) im Intervall \((-90^\circ, 90^\circ]\). Berechnen Sie also den Winkel, für den die Normalspannung maximal ist. Runden Sie auf Rundestellenwert \(0{,}01\). Zeigen Sie, dass:

\[\varphi_1 \stackrel{\small{0{,}01}}{\approx} 63{,}43^\circ\]

Lösung

\[\begin{split}\bar T &= \tfrac12 \left(T_{xx} + T_{yy}\right) \\ &= 2 \\ r &=\sqrt{\left\{ \tfrac12 \left(T_{xx}-T_{yy}\right)\right\}^2 + T_{xy}^2} \\ &= 5\end{split}\]

Damit:

\[\begin{split}\max T_{\bar x \bar x} &= \bar T + r \\ &= 7 \\ \\ \min T_{\bar x \bar x} &= \bar T - r \\ &= -3\end{split}\]

Nach Mohrscher Kreis gilt für den zu \(\max T_{\bar x \bar x}\) gehörigen Winkel:

\[\varphi_1 = \arctan{\tfrac{T_{xy}}{T_{xx} - \min T_{\bar x \bar x}}}\]

Gegeben sind hierbei \(T_{xx}=-1\) sowie \(T_{xy}=4\). Und schon berechnet wurde \(\min T_{\bar x \bar x}=-3,\) so dass:

\[\begin{split}\varphi_1 &= \arctan{}\tfrac{4}{-1 - (-3)} \\ &= \arctan{}2 \\ &\stackrel{\small{0{,}01}}{\approx} 63{,}43^\circ \\\end{split}\]

e) Max. Schubspannung

Zu jedem Winkel \(\varphi\) lässt sich die zugehörige Schubspannung \(T_{\bar x \bar y}(\varphi)\) berechnen. Für einige \(\varphi\) ist \(T_{\bar x \bar y}\) größer, und für andere kleiner. Ermitteln Sie die unter allen \(\varphi\) maximale Schubspannung:

\[\max T_{\bar x \bar y} = \ldots\]

Prüfen Sie Ihr Ergebnis am Mohrschen Kreis.

Berechnen Sie außerdem den zu \(\max T_{\bar x \bar y}\) gehörigen Winkel \(\varphi_1-45^\circ\) im Intervall \((-135^\circ, 45^\circ]\). Berechnen Sie also den Winkel, für den die Schubspannung maximal ist. Runden Sie auf Rundestellenwert \(0{,}01\). Zeigen Sie, dass:

\[\varphi_1 - 45^\circ \stackrel{\small{0{,}01}}{\approx} 18{,}43^\circ\]

Lösung

Es gilt:

\[\begin{split}\max T_{\bar x \bar y} &= r \\ &= 5\end{split}\]

Am Mohrschen Kreis erkennt man, dass der Winkel, für den die Schubspannung maximal ist, um 45 Grad kleiner ist, als der Winkel, für den die Normalspannung maximal ist.

\[\varphi_1 - 45^\circ \stackrel{\small{0{,}01}}{\approx} 18{,}43^\circ\]

Bild zur Aufgabe

Programm

SymPy

Nachfolgend ein Programm, dass Sie ausführen können:

Auf dem PC z.B. mit Anaconda.
Im Browser (online) in drei Schritten:
1. Copy: Source Code in die Zwischenablage kopieren.
2. Paste: Source Code als Python-Notebook einfügen z.B. auf:
  - JupyterLite oder
  - JupyterLab oder
  - Colab.
3. Play: Ausführen.

#!/usr/bin/python3

                  
(x,y)-Comp's of T:
⎡-1  4⎤
⎢     ⎥
⎣4   5⎦
                          
Passive Transformation: φ:
-4°
                  
(x̄,ȳ)-Comp's of T:
⎡-1.53  3.54⎤
⎢           ⎥
⎣3.54   5.53⎦

Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.