1.6.G

../../../_images/1.6.G.png

Gegebene Symbole: \(a, F, G.\)

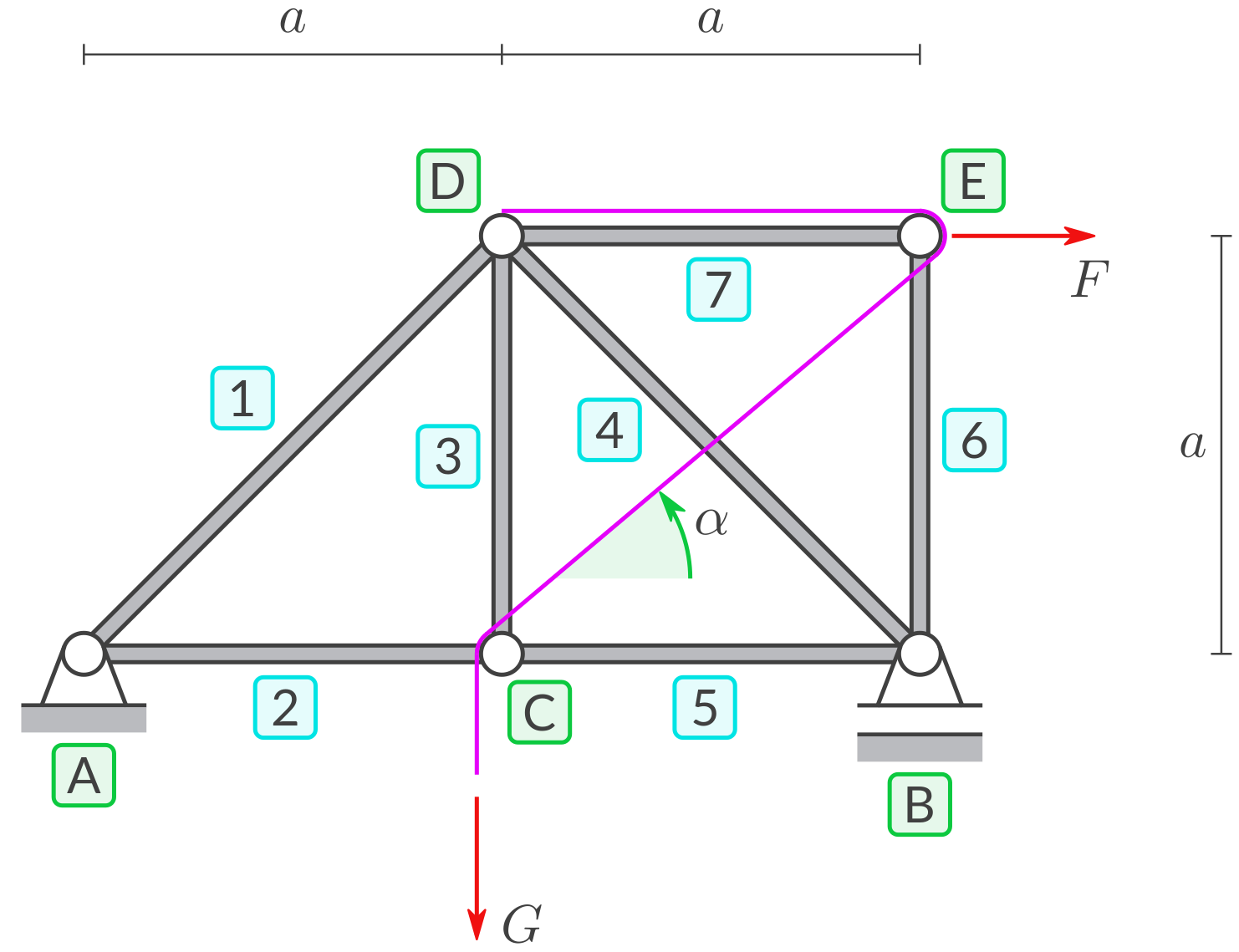
Gegeben ist ein Fachwerk:

  • Am Knoten D ist ein Seil angebracht.

  • Die Gelenke haben keine räumliche Ausdehnung, so dass gilt: \(\alpha=45^\circ.\)

  • Der Kontakt zwischen den Gelenken und dem über die Gelenke gelegten Seil ist reibungslos.

Berechnen Sie die Lagerreaktionen und die Stabkräfte. Gehen Sie wie folgt vor.

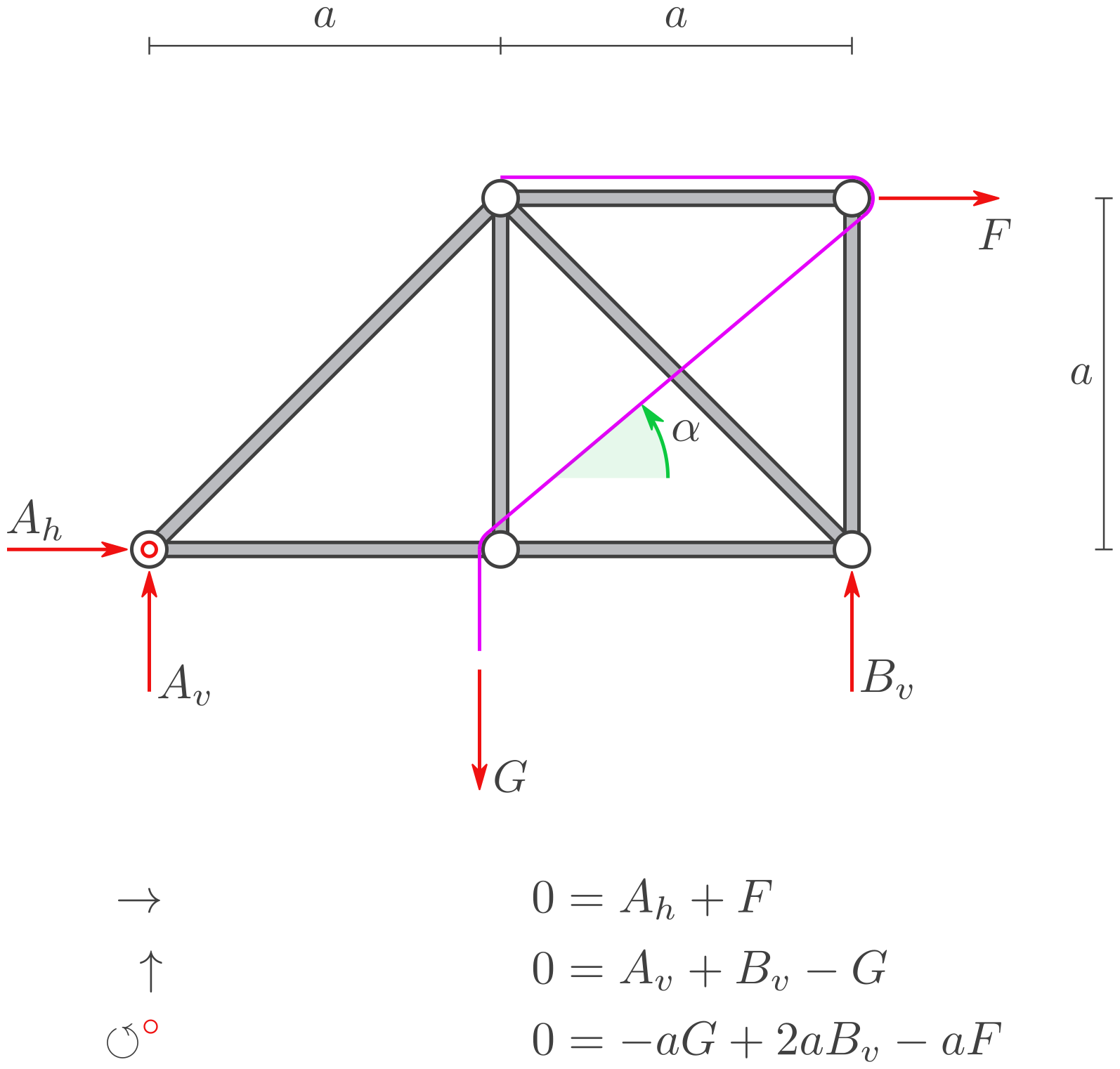
a) Lagerreaktionen

Berechnen Sie die Lagerreaktionen.

Lösung

../../../_images/1.6.G_1.png

Lösung:

\[\begin{split}A_{h} &= - F \\ A_{v} &= - \tfrac{F}{2} + \tfrac{G}{2} \\ B_{v} &= \tfrac{F}{2} + \tfrac{G}{2}\end{split}\]

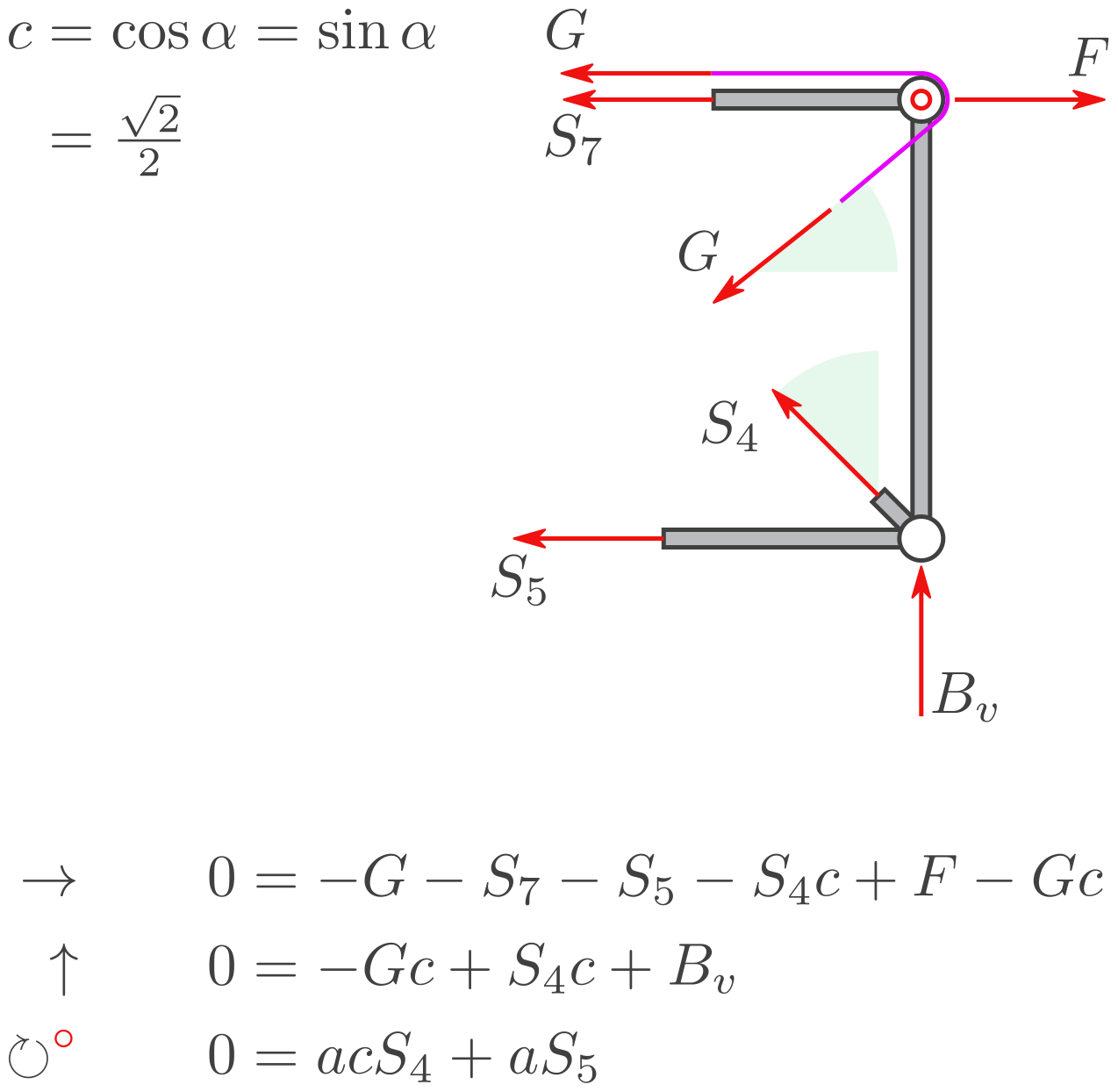
b) Stäbe 4, 5 und 7

Berechnen Sie \(S_4, S_5, S_7\). Schneiden Sie dazu in einem Freischnitt durch alle drei Stäbe.

Lösung

../../../_images/1.6.G_2.png

Lösung:

\[\begin{split}S_{4} &= - \sqrt{2} B_{v} + G \\ S_{5} &= B_{v} - \tfrac{\sqrt{2} G}{2} \\ S_{7} &= F - G - \tfrac{\sqrt{2} G}{2}\end{split}\]

c) Spezialfall

Berechnen Sie \(S_4, S_5, S_7\) für den Fall:

\[F = G = 1 \, \mathrm{N}\]

Lösung

\[\begin{split}S_{4} &= \left(- \sqrt{2} + 1\right)\,\mathrm{N}\\ S_{5} &= \tfrac{1}{2} \left(- \sqrt{2} + 2\right)\,\mathrm{N}\\ S_{7} &= - \tfrac{\sqrt{2}}{2} \,\mathrm{N}\end{split}\]

SymPy

Nachfolgend ein Programm, dass Sie ausführen können:

  • Auf dem PC z.B. mit Anaconda.

  • Im Browser (online) in drei Schritten:

    1. Copy: Source Code in die Zwischenablage kopieren.

    2. Paste: Source Code als Python-Notebook einfügen z.B. auf:

    3. Play: Ausführen.

from sympy import *

a, F, G = var("a, F, G")

Ah, Av, Bv = var('A_h A_v B_v')

eqns = [
    Eq(0, Ah + F),
    Eq(0, Av + Bv - G),
    Eq(0, - G * a + Bv * 2 * a - F * a),
    ]

unknowns = [Bv,Ah,Av]
sol = solve(eqns, unknowns)
pprint(sol)

Bv = sol[Bv]

S4, S5, S7    = var('S4 S5 S7')

c=sqrt(2)/2

eqns = [
    Eq(0, -G - S7 - S5 - S4*c + F - G*c),
    Eq(0, -G*c + S4*c + Bv),
    Eq(0, a*S4*c + a*S5),
    ]

unknowns=[S4, S5, S7]
sol = solve(eqns, unknowns)
pprint(sol)

⎧              F   G      F   G⎫
⎨Aₕ: -F, Aᵥ: - ─ + ─, Bᵥ: ─ + ─⎬
⎩              2   2      2   2⎭
⎧      √2⋅F   √2⋅G          F   √2⋅G   G              √2⋅G⎫
⎨S₄: - ──── - ──── + G, S₅: ─ - ──── + ─, S₇: F - G - ────⎬
⎩       2      2            2    2     2               2  ⎭

Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.