2.1.Q

Video

FEM-Lösung

siehe R2.A

../../../_images/2.1.Q.png — Gegebene *Symbole*: \(F, E, A, l\)

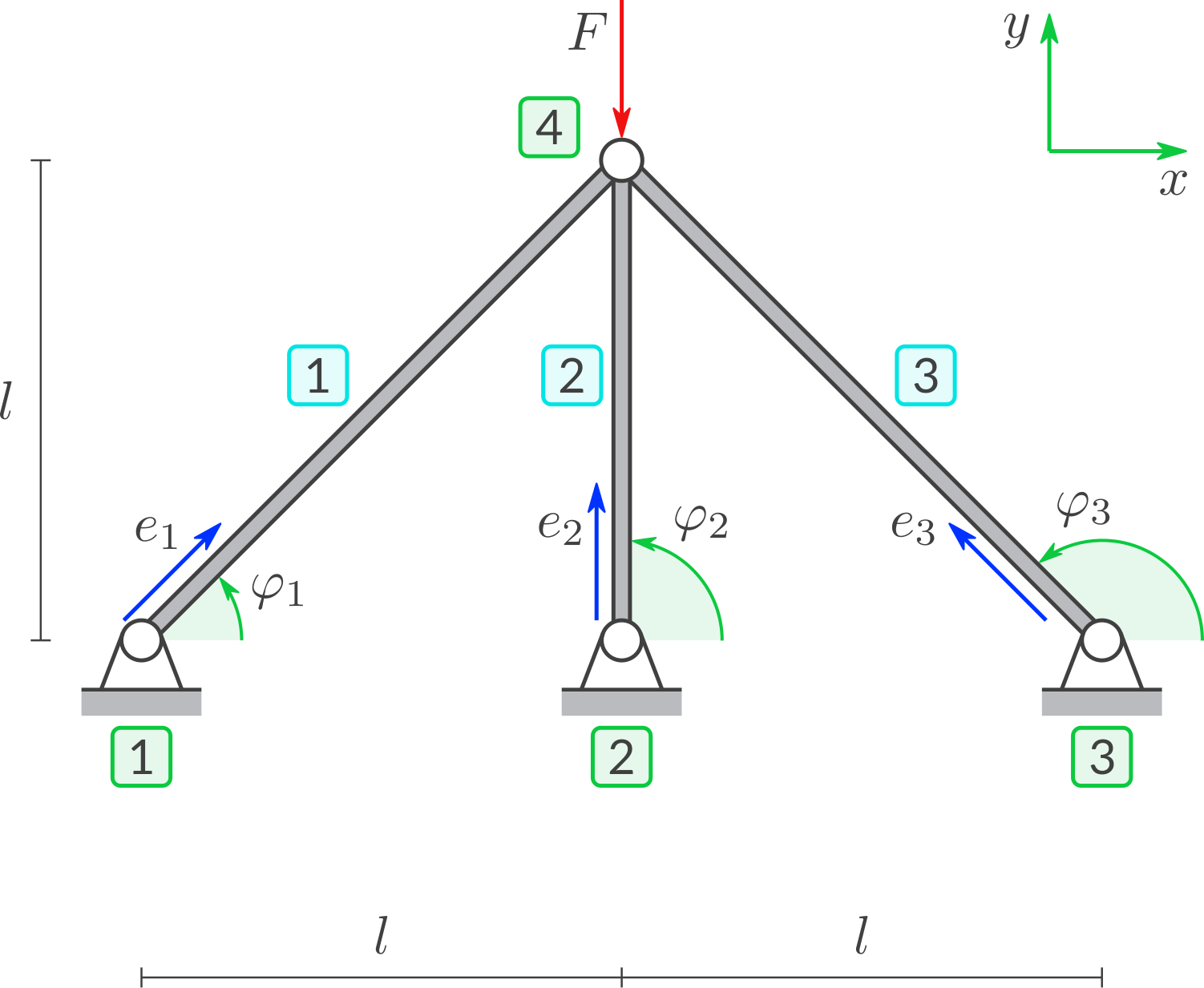
Untersuchen Sie die Struktur aus drei Stäben mit E-Modul \(E\) und Querschnittsfläche \(A\).

Verwenden Sie folgende Abkürzungen:

\begin{align*} \begin{bmatrix} {\color{green}{c_1}} \\ {\color{green}{s_1}} \end{bmatrix} &= \begin{bmatrix} \cos \varphi_1 \\ \sin \varphi_1 \end{bmatrix} \\ \begin{bmatrix} {\color{green}{c_2}} \\ {\color{green}{s_2}} \end{bmatrix} &= \begin{bmatrix} \cos \varphi_2 \\ \sin \varphi_2 \end{bmatrix} \\ \begin{bmatrix} {\color{green}{c_3}} \\ {\color{green}{s_3}} \end{bmatrix} &= \begin{bmatrix} \cos \varphi_3 \\ \sin \varphi_3 \end{bmatrix} \end{align*}

Gehen Sie wie folgt vor:

Lösung auf einer Seite

../../../_images/2.1.Q_all.png — Bezugssystem definieren und Knoten und Stäbe nummerieren. 1. Gleichgewicht, 2. Stab-Einheitsvektoren und (genäherte) Stabverlängerungen, 3. Elastizität, 4. Gleichungssystem und Lösung, 5. Einheiten und Plausibilität prüfen. Gelb = Gegeben. Orange = Unbekannt.

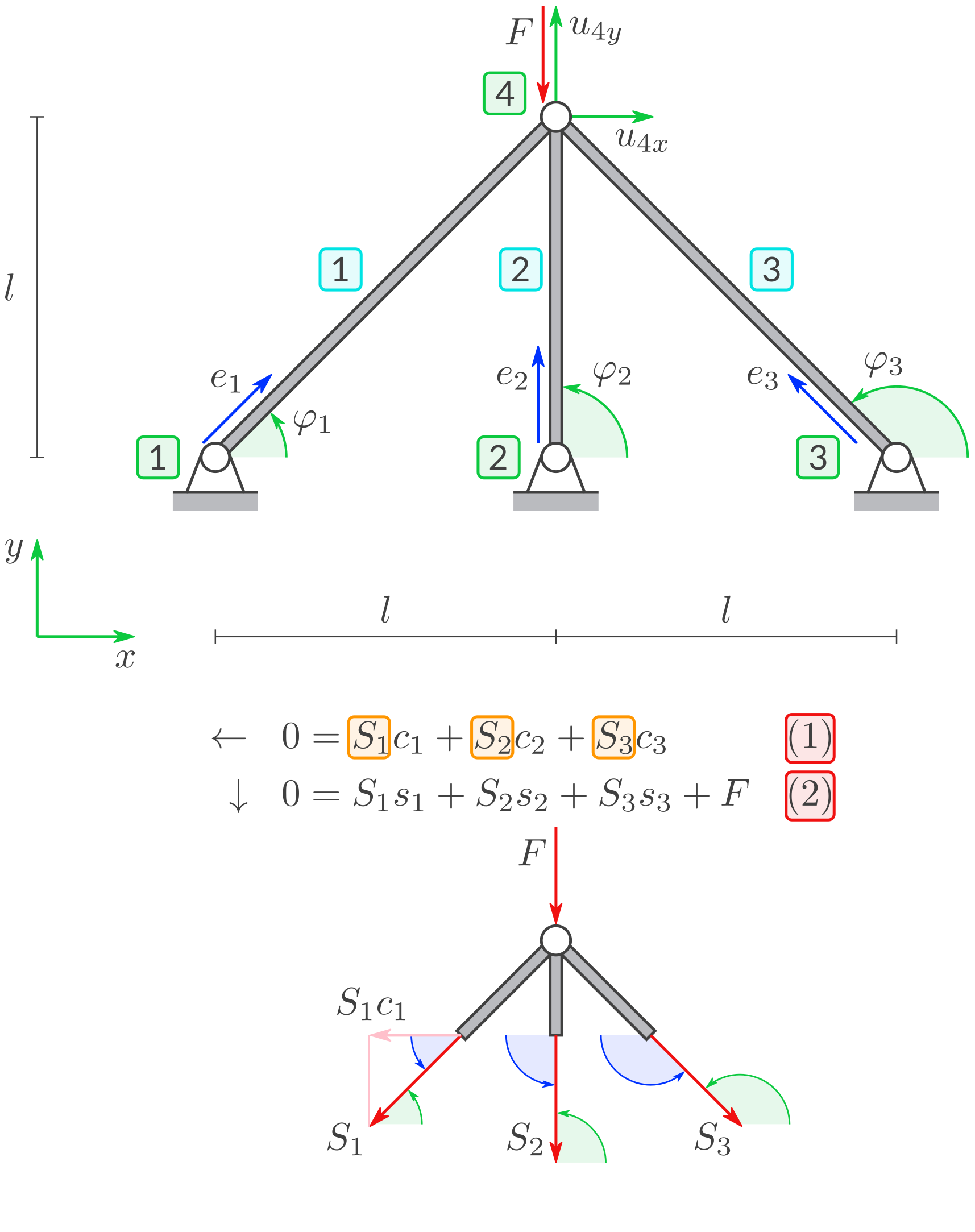
1. Gleichgewicht

Machen Sie einen Knotenschnitt am Knoten 1. Geben Sie zwei Gleichgewichtsbedingungen an.

Lösung

2. Kinematik: Einheitsvektoren und Verlängerungen

Geben Sie die (genäherten) Stabverlängerungen \(\Delta l_1, \Delta l_2, \Delta l_3\) an abhängig von den \((x,y)\)-Komponenten \((u_{4x}, u_{4y})\) des Verschiebungsvektors \(\boldsymbol u_4\) von Knoten 4.

Lösung

\((x,y)\)-Komponenten der Einheitsvektoren:

\begin{align*} \begin{bmatrix} e_{1x} \\ e_{1y} \end{bmatrix} &= \begin{bmatrix} {\color{green}{c_1}} \\ {\color{green}{s_1}} \end{bmatrix} \\ \begin{bmatrix} e_{2x} \\ e_{2y} \end{bmatrix} &= \begin{bmatrix} {\color{green}{c_2}} \\ {\color{green}{s_2}} \end{bmatrix} \\ \begin{bmatrix} e_{3x} \\ e_{3y} \end{bmatrix} &= \begin{bmatrix} {\color{green}{c_3}} \\ {\color{green}{s_3}} \end{bmatrix} \end{align*}

Stabverlängerungen:

\begin{align*} \Delta l_1 &= \begin{bmatrix} {\color{green}{c_1}} & {\color{green}{s_1}} \end{bmatrix} \begin{bmatrix} u_{4x} \\ u_{4y} \end{bmatrix} \\ &= \begin{bmatrix} \tfrac{\sqrt2}{2} & \tfrac{\sqrt2}{2} \end{bmatrix} \begin{bmatrix} u_{4x} \\ u_{4y} \end{bmatrix} \\ &= \tfrac{\sqrt2}{2} (u_{4x} + u_{4y})\tag{3} \\ \Delta l_2 &= \begin{bmatrix} {\color{green}{c_2}} & {\color{green}{s_2}} \end{bmatrix} \begin{bmatrix} u_{4x} \\ u_{4y} \end{bmatrix} \\ &= \begin{bmatrix} 0 & 1 \end{bmatrix} \begin{bmatrix} u_{4x} \\ u_{4y} \end{bmatrix} \\ &= u_{4y}\tag{4} \\ \Delta l_3 &= \begin{bmatrix} {\color{green}{c_3}} & {\color{green}{s_3}} \end{bmatrix} \begin{bmatrix} u_{4x} \\ u_{4y} \end{bmatrix} \\ &= \begin{bmatrix} \tfrac{-\sqrt2}{2} & \tfrac{\sqrt2}{2} \end{bmatrix} \begin{bmatrix} u_{4x} \\ u_{4y} \end{bmatrix} \\ &= \tfrac{\sqrt2}{2} (-u_{4x} + u_{4y})\tag{5} \end{align*}

3. Elastizität

Geben Sie die genäherten Stabverlängerungen an abhängig von den Stab-Zugkräften und den gegebenen Symbolen.

Lösung

Die Stäbe 1 und 3 haben die Länge \(\sqrt 2 l\). Und Stab 2 hat die Länge \(l\).

\begin{align} \Delta l_1 &= \tfrac{S_1}{EA} \sqrt 2 l \tag{6}\\ \Delta l_2 &= \tfrac{S_2}{EA} l \tag{7}\\ \Delta l_3 &= \tfrac{S_3}{EA} \sqrt 2 l \tag{8} \end{align}

4. Gleichungssystem und Lösung

Berechnen Sie abhängig von den gegebenen Symbolen:

\begin{align*} S_1 &= \ldots F \\ S_2 &= \ldots F \\ S_3 &= \ldots F \\ \Delta l_1 &= \ldots \frac{Fl}{EA} \\ \Delta l_2 &= \ldots \frac{Fl}{EA} \\ \Delta l_3 &= \ldots \frac{Fl}{EA} \\ u_{4x} &= \ldots \frac{Fl}{EA} \\ u_{4y} &= \ldots \frac{Fl}{EA} \end{align*}

Berechnen Sie außerdem \(u_{4y}\) für folgende Größen:

\begin{align*} F &= 5\,\mathrm{kN} \\ E &= 200\,\mathrm{GPa} \\ A &= 25\,\mathrm{mm}^2 \\ l &= 1707\,\mathrm{mm} \end{align*}

Und zwar in \(\mathrm{mm}\) (Millimeter) und gerundet auf Rundestellenwert \(0{,}0001\):

\[u_{4y} \stackrel{0{,}0001}{\approx} \ldots \, \mathrm{mm}\]

Lösung

8 Gleichungen zur Berechnung der 8 Unbekannten \((S_1, S_2, S_3, \Delta l_1, \Delta l_2, \Delta l_3, u_{4x}, u_{4y})\):

\begin{align*} 0 &= S_1 c_1 - S_3 c_1 \tag{1}\\ 0 &= F + S_1 c_1 + S_2 + S_3 c_1 \tag{2}\\ \Delta l_1 &= \tfrac{\sqrt2}{2} (u_{4x} + u_{4y}) \tag{3}\\ \Delta l_2 &= u_{4y} \tag{4} \\ \Delta l_3 &= \tfrac{\sqrt2}{2} (-u_{4x} + u_{4y})\tag{5}\\ \Delta l_1 &= \tfrac{S_1}{EA} \sqrt 2 l \tag{6}\\ \Delta l_2 &= \tfrac{S_2}{EA} l \tag{7}\\ \Delta l_3 &= \tfrac{S_3}{EA} \sqrt 2 l\tag{8} \end{align*}

Lösung:

\begin{align*} S_1 &= \left(-1 + \frac{\sqrt{2}}{2} \right) F \notag \\ S_2 &= \left(-2 + \sqrt{2} \right) F \notag \\ S_3 &= \left(-1 + \frac{\sqrt{2}}{2} \right) F \notag \\ \Delta l_1 &= \left( - \sqrt{2} + 1 \right) \frac{Fl}{EA} \notag \\ \Delta l_2 &= \left( -2 + \sqrt{2} \right) \frac{Fl}{EA} \notag \\ \Delta l_3 &= \left( - \sqrt{2} + 1 \right) \frac{Fl}{EA} \notag \\ u_{4x} &= 0 \cdot \frac{Fl}{EA}\notag \\ u_{4y} &= \left( -2 + \sqrt{2} \right) \frac{Fl}{EA} \notag \\ \notag \\ u_{4y} &\stackrel{0{,}0001}{\approx} -0{,}9999\,\mathrm{mm} \end{align*}

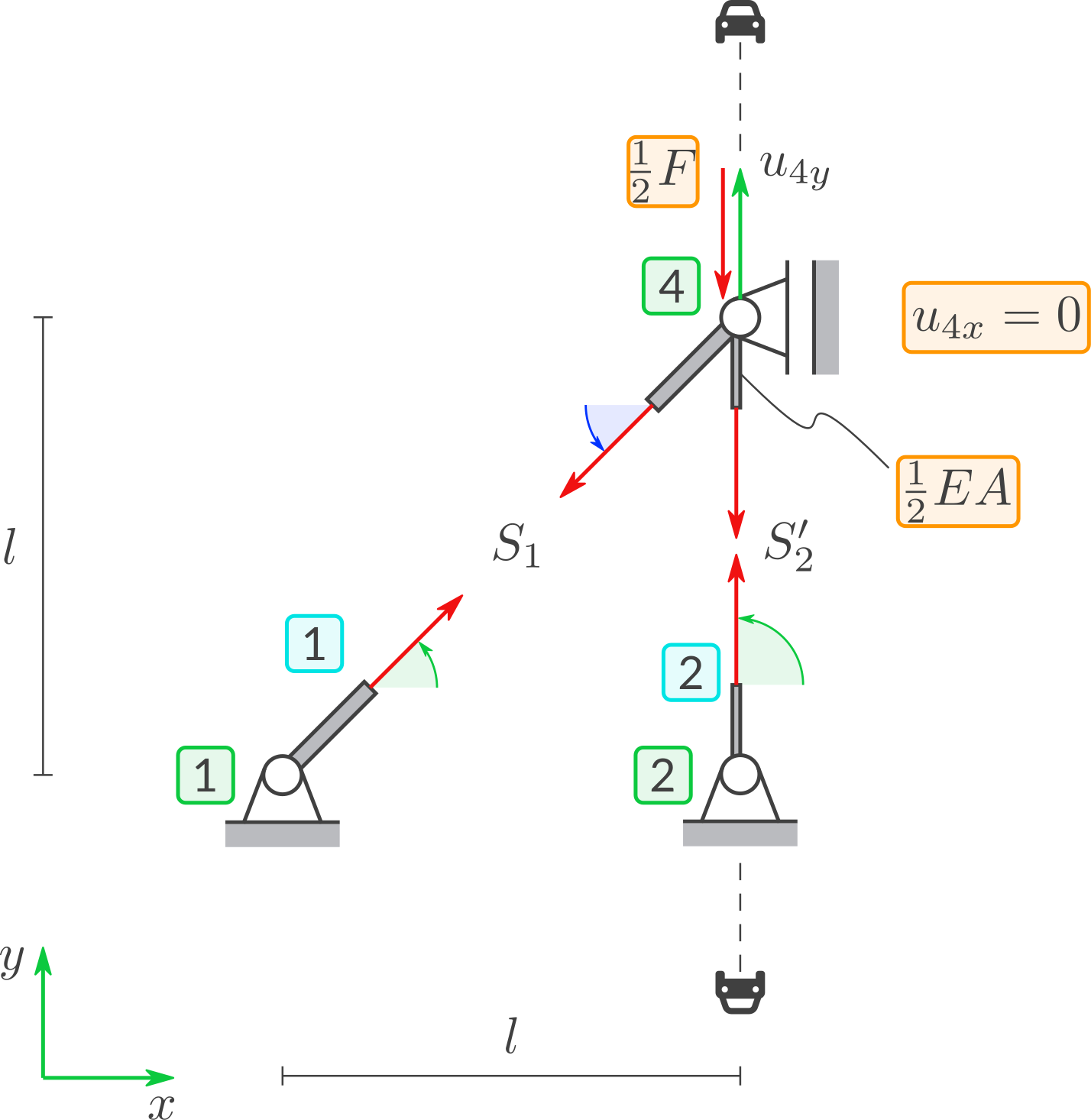
5. Symmetrie

Zeigen Sie, dass Sie bei Ausnutzung der Symmetrie dieselbe Lösung erhalten.

Lösung

6 Gleichungen zur Berechnung der 6 Unbekannten \((S_1, S_2', \Delta l_1, \Delta l_2, u_{4x}, u_{4y})\) und Lösung:

\begin{align*} 0 &= u_{4x} \tag{1}\\ 0 &= \tfrac 1 2 F + S_1 c_1 + S_2' \tag{2} \\ \Delta l_1 &= \tfrac{\sqrt2}{2} (u_{4x} + u_{4y}) \tag{3} \\ \Delta l_2 &= u_{4y} \tag{4} \\ \Delta l_1 &= \tfrac{S_1}{EA} \sqrt 2 l \tag{5} \\ \Delta l_2 &= \tfrac 1 2 \tfrac{S_2}{EA} l \tag{6} \\ \notag\\ S_1 &= \left(-1 + \frac{\sqrt{2}}{2} \right) F \notag \\ S_2' &= \tfrac 1 2 \left(-2 + \sqrt{2} \right) F = \tfrac12 S_2 \notag \\ \Delta l_1 &= \left( - \sqrt{2} + 1 \right) \frac{Fl}{EA} \notag \\ \Delta l_2 &= \left( -2 + \sqrt{2} \right) \frac{Fl}{EA} \notag \\ u_{4x} &= 0 \cdot \frac{Fl}{EA}\notag \\ u_{4y} &= \left( -2 + \sqrt{2} \right) \frac{Fl}{EA} \notag \end{align*}

SymPy

Nachfolgend ein Programm, dass Sie ausführen können:

Auf dem PC z.B. mit Anaconda.
Im Browser (online) in drei Schritten:
1. Copy: Source Code in die Zwischenablage kopieren.
2. Paste: Source Code als Python-Notebook einfügen z.B. auf:
  - JupyterLite oder
  - JupyterLab oder
  - Colab.
3. Play: Ausführen.

from sympy.physics.units import *
from sympy import *

# Units:
(mm, cm)  =  ( m/1000, m/100 )
kN        =  10**3*newton
Pa        =  newton/m**2
MPa       =  10**6*Pa
GPa       =  10**9*Pa
deg       =  pi/180
half      =  S(1)/2

# Rounding:
import decimal
from decimal import Decimal as DX
from copy import deepcopy
def iso_round(obj, pv,
    rounding=decimal.ROUND_HALF_EVEN):
    import sympy
    """
    Rounding acc. to DIN EN ISO 80000-1:2013-08
    place value = Rundestellenwert
    """
    assert pv in set([
        # place value   #  round to:
        "1",              #  round to integer
        "0.1",            #  1st digit after decimal
        "0.01",           #  2nd
        "0.001",          #  3rd
        "0.0001",         #  4th
        "0.00001",        #  5th
        "0.000001",       #  6th
        "0.0000001",      #  7th
        "0.00000001",     #  8th
        "0.000000001",    #  9th
        "0.0000000001",   # 10th
        ])
    objc = deepcopy(obj)
    try:
        tmp = DX(str(float(objc)))
        objc = tmp.quantize(DX(pv), rounding=rounding)
    except:
        for i in range(len(objc)):
            tmp = DX(str(float(objc[i])))
            objc[i] = tmp.quantize(DX(pv), rounding=rounding)
    return objc

# Parameters:
F, E, A, l = var("F, E, A, l")
EA = E*A

# Shortcuts:
p1, p2, p3 = 45 *deg, 90 *deg, 135 *deg
c1, c2, c3 = cos(p1), cos(p2), cos(p3)
s1, s2, s3 = sin(p1), sin(p2), sin(p3)

r = sqrt(2)
c = r / 2

# Symbols:
S1, S2, S2p, S3    = var("S1, S2, S2p, S3")
dl1, dl2, dl3 = var("dl1, dl2, dl3")
u4x, u4y      = var("u4x, u4y")

sub_list = [
    ( F,        5 *kN     ),
    ( E,      200 *GPa    ),
    ( A,       25 *mm**2  ),
    ( l,     1707 *mm     ),
    ]

symm = True
symm = False

# Equations:
if not symm:
    unks = [S1, S2, S3, dl1, dl2, dl3, u4x, u4y]
    eqns = [
        Eq(  0, S1*c1 + S2*c2 + S3*c3       ),
        Eq(  0, S1*s1 + S2*s2 + S3*s3 + F   ),
        Eq(          dl1 ,  c*( u4x + u4y)  ),
        Eq(          dl2 ,  u4y             ),
        Eq(          dl3 ,  c*(-u4x + u4y)  ),
        Eq(          dl1 ,  S1/EA * r*l     ),
        Eq(          dl2 ,  S2/EA * l       ),
        Eq(          dl3 ,  S3/EA * r*l     ),
        ]
else:
    unks = [S1, S2p, dl1, dl2, u4x, u4y]
    eqns = [
        Eq(             0,  u4x             ),
        Eq(    0, S1*s1 + S2p + F/2         ), 
        Eq(          dl1 ,  c*( u4x + u4y)  ),
        Eq(          dl2 ,  u4y             ),
        Eq(          dl1 ,  S1/EA * r*l     ),
        Eq(          dl2 ,  S2p/(EA/2) * l  ),
        ]

sol = solve(eqns, unks)
fac = F*l / EA
if not symm:
    S1, S2, S3, dl1, dl2, dl3, u4x, u4y = \
        sol[S1],sol[S2],sol[S3],sol[dl1],sol[dl2],sol[dl3],sol[u4x],sol[u4y]

    pprint("\n(S₁, S₂, S₃) / F:")
    for S in [S1, S2, S3]:
        tmp = S / F
        tmp = tmp.simplify()
        pprint(tmp)

    pprint("\n(Δl₁, Δl₂, Δl₃) / ( Fl / (EA) ):")
    for s in [dl1, dl2, dl3]:
        tmp = s / fac
        tmp = tmp.simplify()
        pprint(tmp)
    pprint("\n(u4x, u4y) / ( Fl / (EA) ):")
    tmp = Matrix([u4x, u4y])
    tmp /= fac
    tmp = tmp.applyfunc(simplify)
    pprint(tmp)
    pprint("\nu4y / mm:")
    tmp = u4y
    tmp = tmp.subs(sub_list)
    tmp /= mm
    tmp = iso_round(tmp,"0.0001")
    pprint(tmp)

elif symm:
    S1, dl1, dl2, u4x, u4y = \
        sol[S1],sol[dl1],sol[dl2],sol[u4x],sol[u4y]
    S2p = sol[S2p]
    pprint("\n(S₁, S₂') / F:")
    for S in [S1, S2p]:
        tmp = S / F
        tmp = tmp.simplify()
        pprint(tmp)

    pprint("\n(Δl₁, Δl₂) / (Fl/EA):")
    for s in [dl1, dl2]:
        tmp = s / fac
        tmp = tmp.simplify()
        pprint(tmp)

    pprint("\n(u4x, u4y) / (Fl/EA):")
    tmp = Matrix([u4x, u4y])
    tmp /= fac
    tmp = tmp.simplify()
    pprint(tmp)

    pprint("\nu4y / mm:")
    tmp = u4y
    tmp = tmp.subs(sub_list)
    tmp /= mm
    tmp = iso_round(tmp,"0.0001")
    pprint(tmp)

                 
(S₁, S₂, S₃) / F:
     √2
-1 + ──
     2 
-2 + √2
     √2
-1 + ──
     2 
                                
(Δl₁, Δl₂, Δl₃) / ( Fl / (EA) ):
1 - √2
-2 + √2
1 - √2
                           
(u4x, u4y) / ( Fl / (EA) ):
⎡   0   ⎤
⎢       ⎥
⎣-2 + √2⎦
         
u4y / mm:
-0.9999

Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.