2.4.2.I

Video

Lösung auf einer Seite

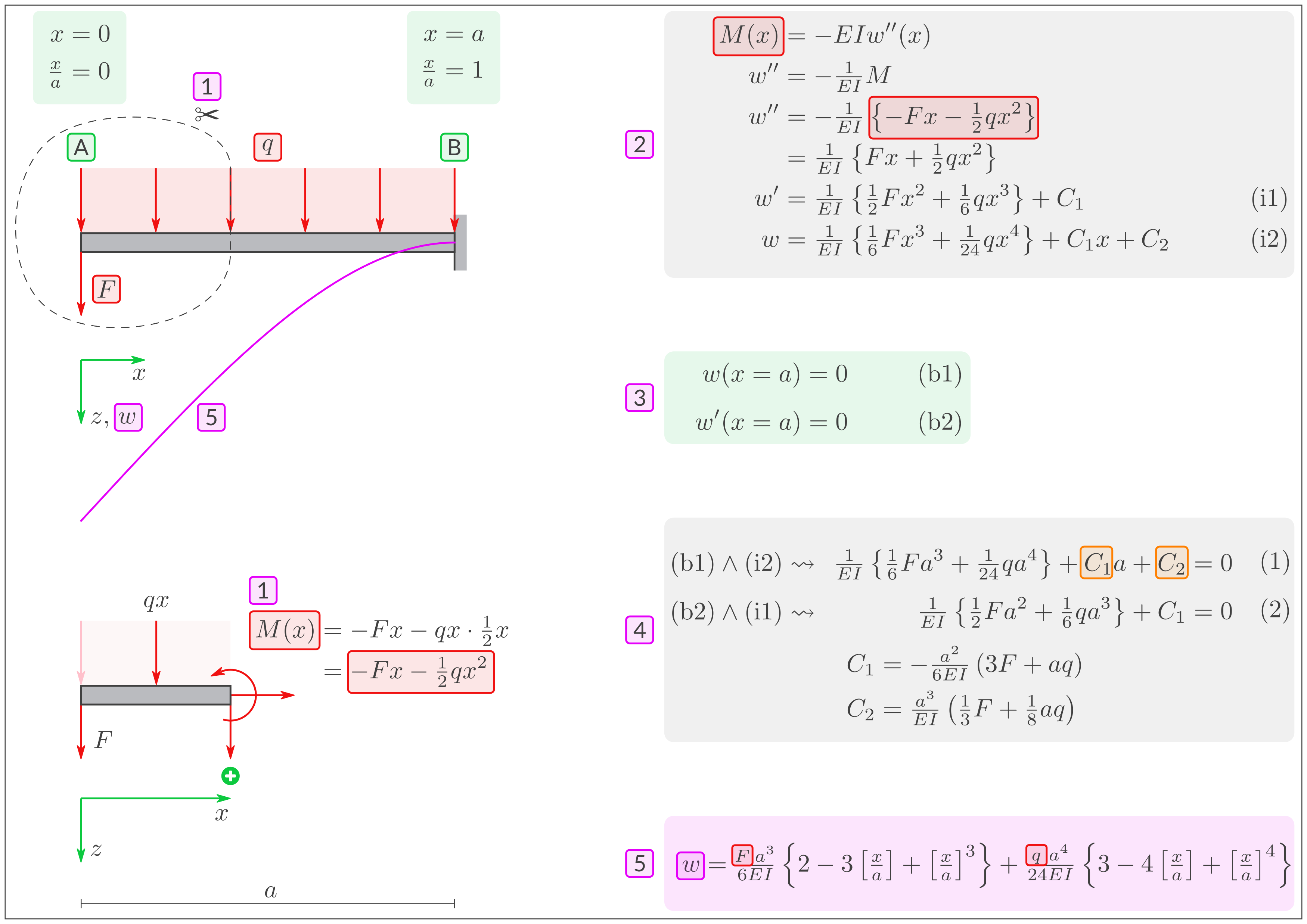
../../../../_images/2.4.2.I_all.png — 1: Freischneiden und \(M\) berechnen. 2: Integrieren zur allgemeinen Lösung. 3: Randbedingungen in \(w\) und \(w'\). 4: Integrationskonstanten berechnen. 5: Spezielle Lösung \(w\).

FEM-Lösung

siehe B2.D

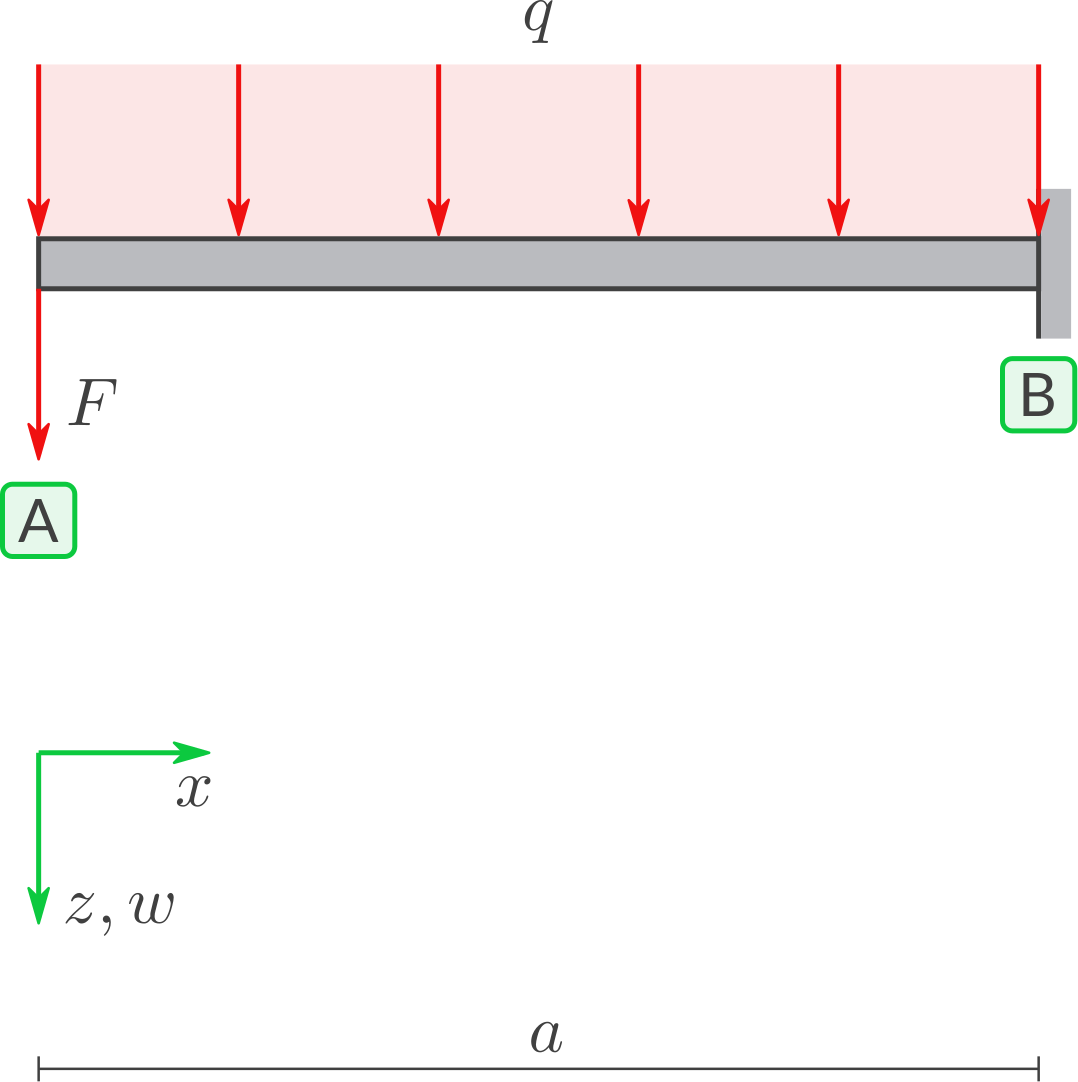
../../../../_images/2.4.2.I.png — Gegebene *Symbole*: \(a, q, F, E, I.\)

Gegeben ist ein rechts bei B eingespannter Balken, auf den äußere Lasten wirken.

Gegebene Größen:

\[\begin{split}a &= 3 \, \mathrm{m} \\ q &= 3 \, \tfrac{\mathrm{kN}}{\mathrm{m}} \\ F &= 10 \, \mathrm{kN} \\ E &= 200 \, \mathrm{GPa} \\ I &= 6500 \, \mathrm{cm}^4\end{split}\]

1. Biegesteifigkeit

Für die gegebenen Größen: Berechnen Sie die Biegesteifigkeit \(B\) in \(\mathrm{kNm}^2\):

\[\begin{split}B &= EI \\ &= \dots \,\mathrm{kNm}^2\end{split}\]

Lösung

\[B = 13000 \,\mathrm{kNm}^2\]

2. Biegemoment

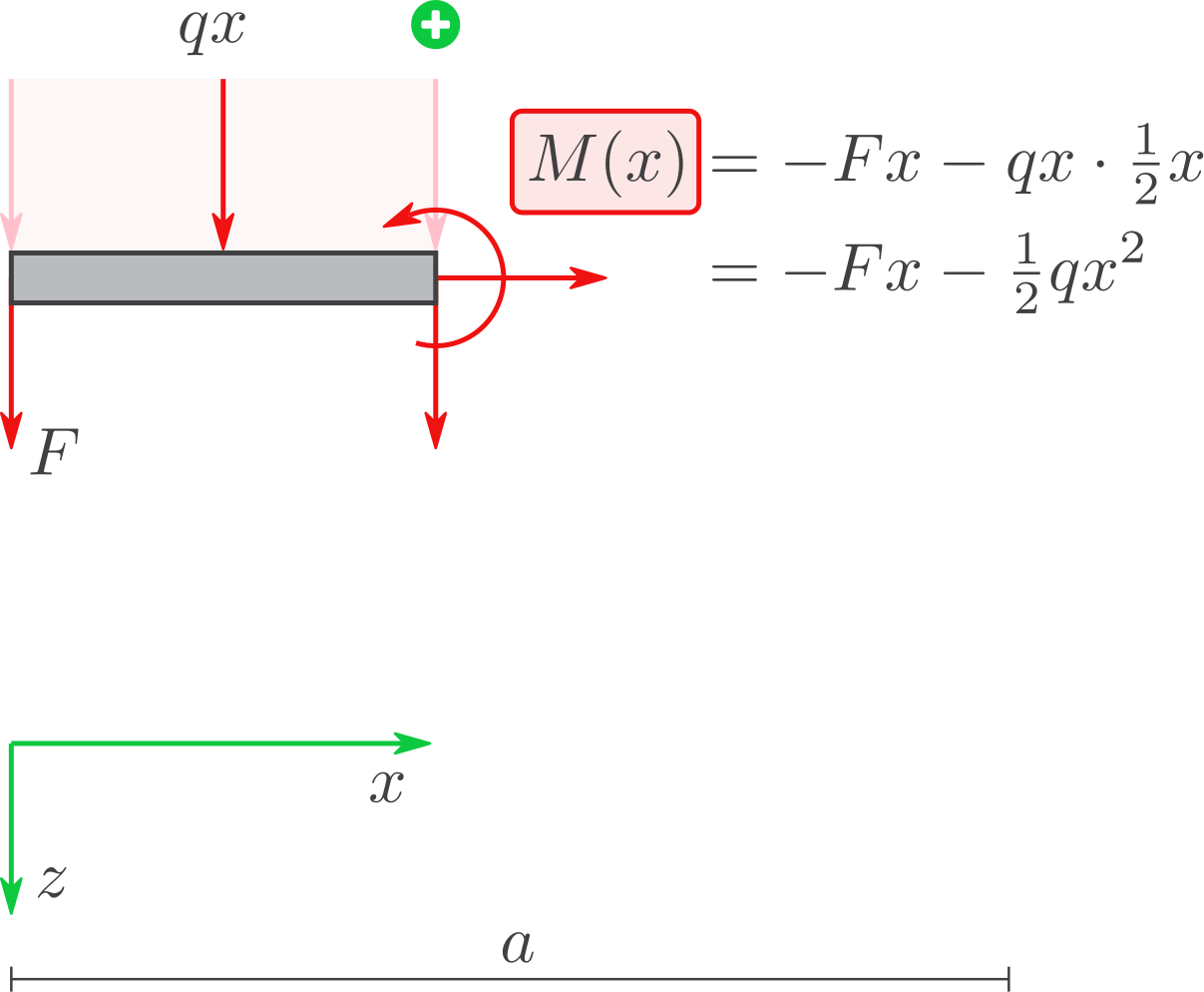
Berechnen Sie das Biegemoment \(M\):

für die gegebenen Symbole als Funktion \(M(x)\) und
für die gegebenen Größen, und zwar bei \(x = 3\,\mathrm{m}.\)

Lösung

Für die gegebenen Symbole:

\begin{align*} M(x) = - \tfrac{1}{2} x \left(2 F + q x\right) \end{align*}

Für die gegebenen Größen und nach Einsetzen von \(x=3\,\mathrm{m}\):

\[\begin{split}M(x = 3\mathrm{m}) &= - \tfrac{87}{2} \,\mathrm{kNm} \\ &= - 43{,}5 \,\mathrm{kNm}\end{split}\]

3. Integration und allgemeine Lösung

Für die gegebenen Symbole: Zeigen Sie, dass:

\begin{align*} w= \tfrac{1}{E I} \left\{ \tfrac{1}{6} F x^{3} + \tfrac{1}{24} q x^{4} \right\} + C_{1} x + C_{2} \end{align*}

mit zwei Konstanten \(C_1, C_2\).

Lösung

Ausgehend von:

\[M(x) = - EI w''(x)\]

Einsetzen von \(M(x)=- \tfrac{1}{2} x \left(2 F + q x\right)\) und Integration liefert:

\begin{align} \label{eq-2.4.2.I-i} M(x) &= - EI w''(x) \\ \\ w'' &= - \tfrac{1}{EI} M \\ &= - \tfrac{1}{EI} \left\{- F x - \tfrac{1}{2} q x^2 \right\} \notag \\ &= \tfrac{1}{EI} \left\{ F x + \tfrac{1}{2} q x^2 \right\} \notag \\ \\ w' &= \tfrac{1}{EI} \left\{\tfrac 1 2 F x^2 + \tfrac{1}{6} q x^3 \right\} + C_1 \tag{i1} \\ \\ w &= \tfrac{1}{E I} \left\{ \tfrac{1}{6} F x^{3} + \tfrac{1}{24} q x^{4} \right\} + C_{1} x + C_{2} \tag{i2} \end{align}

mit \(C_1\) und \(C_2\) als Integrationskonstanten. Die letzte Gleichung heißt allgemeine Lösung.

4. Randbedingungen und spezielle Lösung

Geben Sie Randbedingungen an. Zeigen Sie, dass die Auswertung der Randbedingungen auf folgende Integrationskonstanten führt:

\[\begin{split}C_1 &= - \tfrac{a^{2}}{6 EI} \left(3 F + a q\right) \\ C_2 &= \tfrac{a^{3}}{EI} \left(\tfrac{1}{3} F + \tfrac{1}{8} a q\right)\end{split}\]

Zeigen Sie, dass:

\[\begin{split}w &= \tfrac{F a^3}{6 E I}\left\{ 2 - 3 \left[\tfrac x a \right] + \left[\tfrac x a \right]^3 \right\} \dots \\ \dots &+ \tfrac{q a^4}{24 E I}\left\{ 3 - 4 \left[\tfrac x a \right] + \left[\tfrac x a \right]^4 \right\}\end{split}\]

Lösung

Randbedingungen am rechten Rand bei \(x=a\):

\begin{align} \label{eq-2.4.2.I-b} w(x=a) &= 0 \tag{b1}\\ w'(x=a)&= 0 \tag{b2} \end{align}

Auswerten der Funktionen (i2) an der Stelle \(x=a\) und Verwendung von (b1) liefert:

\[w(x=a) = \tfrac{1}{E I} \left\{ \tfrac{1}{6} F a^{3} + \tfrac{1}{24} q a^{4} \right\} + C_{1} a + C_{2} \stackrel{!}{=} 0\]

Auswerten der Funktionen (i1) an der Stelle \(x=a\) und Verwendung von (b2) liefert:

\[w'(x=a) = \tfrac{1}{EI} \left\{\tfrac 1 2 F a^2 + \tfrac{1}{6} q a^3 \right\} + C_1 \stackrel{!}{=} 0\]

Und aus diesen beiden Gleichungen lassen sich \(C_1\) und \(C_2\) berechnen. Lösung:

\begin{align} C_1 &= - \tfrac{a^{2}}{6 EI} \left(3 F + a q\right) \\ C_2 &= \tfrac{a^{3}}{EI} \left(\tfrac{1}{3} F + \tfrac{1}{8} a q\right) \end{align}

Einsetzen dieser \(C_1, C_2\) in die allgemeine Lösung liefert die spezielle Lösung:

\begin{align} \label{eq-2.4.2.I-S} w = \tfrac{Fa^3}{6 E I}\left\{ 2 - 3 \left[\tfrac x a \right] + \left[\tfrac x a \right]^3 \right\} + \tfrac{qa^4}{24 E I}\left\{ 3 - 4 \left[\tfrac x a \right] + \left[\tfrac x a \right]^4 \right\} \tag{1} \end{align}

5. Funktionsgraph der w-Funktion

Für die gegebenen Größen: Zeichnen Sie \(w\) in \(\mathrm{mm}\) (Millimeter) über \(x\) in \(\mathrm{m}\) (Meter) - und zwar für verschiedene \(-10\,\mathrm{kN} < F <10\,\mathrm{kN}\) und verschiedene \(-3 \, \tfrac{\mathrm{kN}}{\mathrm{m}} < q < 3 \, \tfrac{\mathrm{kN}}{\mathrm{m}}.\)

Lösung

Bokeh Plot

6. Ergebnisse für Größen

Für die gegebenen Größen: Berechnen Sie die Querverschiebung \(w\) und deren Ableitung \(w'\) bei \(x=0\,\mathrm{m}\). Runden Sie auf Rundestellenwert \(0{,}01\) bzw. \(0{,}0001\). Zeigen Sie, dass:

\[\begin{split}w(0) &\stackrel{0{,}01}{\approx} 9{,}26 \,\mathrm{mm} \\ w'(0) &\stackrel{0{,}0001}{\approx} -0{,}0045\end{split}\]

Berechnen Sie außerdem den Neigungswinkel \(\psi\) bei \(x=0\) in \(^\circ\) (Grad) und gerundet auf \(0{,}0001\). Zeigen Sie, dass:

\[\begin{split}\psi(0) &= - w'(0) \\ &\stackrel{0{,}0001}{\approx} 0{,}2578^\circ\end{split}\]

Lösung

Auswertung von (1) bei \(x=0\) liefert:

\[w(0)\stackrel{0{,}01}{\approx} 9{,}26\,\mathrm{mm}\]

Ableitung von \(w(x)\) liefert:

\[\begin{split}w' &= \tfrac{F a^2}{6 E I}\left\{ - 3 + 3 \left[\tfrac x a \right]^2 \right\} \dots \\ \dots &+ \tfrac{q a^3}{24 E I}\left\{ - 4 + 4 \left[\tfrac x a \right]^3 \right\}\end{split}\]

Auswertung bei \(x=0\) und Einsetzen der gegebenen Größen liefert:

\[w'(0) = -0{,}00450\]

Neigungswinkel bei \(x=0\):

\[\begin{split}\psi(0) &= - w'(0)\\ &= 0{,}0045 \tfrac{180^\circ}{\pi} \\ &\stackrel{0{,}0001}{\approx} 0{,}2578^\circ\end{split}\]

7. Ergebnis-Kontrolle

Überprüfen Sie Ihrer Ergebnisse. Zeigen Sie dazu, dass:

\[\begin{split}w(a) &= 0 \\ w'(a) &= 0\end{split}\]

Lösung

Auswerten der speziellen Lösung \(w\) bzw. (1) und der Ableitung \(w'\) bei \(x=a\) liefert:

\[\begin{split}w(a) &= 0 \\ w'(a) &= 0\end{split}\]

8. Spezialfall

Für die gegebenen Symbole: Berechnen Sie \(F\) abhängig von \(qa\), so dass die Querverschiebung \(w(0)\) am linken Rand Null ist.

Lösung

Auswertung von (1) bei \(x=0\) führt auf:

\[\begin{split}w(0) = 2 F\tfrac{a^3}{6 E I} + 3 q \tfrac{a^4}{24 E I} &\stackrel{!}{=} 0 \\ \tfrac 1 3 F &= - \tfrac 1 8 q a \\ F &= -\tfrac 3 8 q a\end{split}\]

SymPy

Nachfolgend ein Programm, dass Sie ausführen können:

Auf dem PC z.B. mit Anaconda.
Im Browser (online) in drei Schritten:
1. Copy: Source Code in die Zwischenablage kopieren.
2. Paste: Source Code als Python-Notebook einfügen z.B. auf:
  - JupyterLite oder
  - JupyterLab oder
  - Colab.
3. Play: Ausführen.

from sympy.physics.units import *
from sympy import *

# Units:
(mm, cm)  =  ( m/1000, m/100 )
kN        =  10**3*newton
Pa        =  newton/m**2
MPa       =  10**6*Pa
GPa       =  10**9*Pa
deg       =  pi/180
half      =  S(1)/2

# Rounding:
import decimal
from decimal import Decimal as DX
from copy import deepcopy
def iso_round(obj, pv,
    rounding=decimal.ROUND_HALF_EVEN):
    import sympy
    """
    Rounding acc. to DIN EN ISO 80000-1:2013-08
    place value = Rundestellenwert
    """
    assert pv in set([
        # place value   #  round to:
        "1",              #  round to integer
        "0.1",            #  1st digit after decimal
        "0.01",           #  2nd
        "0.001",          #  3rd
        "0.0001",         #  4th
        "0.00001",        #  5th
        "0.000001",       #  6th
        "0.0000001",      #  7th
        "0.00000001",     #  8th
        "0.000000001",    #  9th
        "0.0000000001",   # 10th
        ])
    objc = deepcopy(obj)
    try:
        tmp = DX(str(float(objc)))
        objc = tmp.quantize(DX(pv), rounding=rounding)
    except:
        for i in range(len(objc)):
            tmp = DX(str(float(objc[i])))
            objc[i] = tmp.quantize(DX(pv), rounding=rounding)
    return objc


a, q, F, E, I = var('a, q, F, E, I')

sub_list = [
    (a, 3 *m),
    (q, 3 *kN/m),
    (F, 10 *kN),
    (E, 200 *GPa),
    (I, 65*10**6 *mm**4)
    ]

pprint("EI / kNm²:")
B = E*I
tmp = B
tmp = tmp.subs(sub_list)
tmp /= kN*m**2
pprint(tmp)

pprint("\nM:")
x = var("x")
M = - F * x - q*x*x/2
M = M.simplify()
tmp = M
pprint(tmp)

pprint("\nM(x = 3 m)/ kNm:")
tmp = tmp.subs(sub_list)
tmp = tmp.subs(x, 3*m)
tmp /= kN*m
tmp = tmp.simplify()
pprint(tmp)

pprint("Integrating...")
C1, C2 = var('C1, C2')
xi = var("xi")

# w'' = - M / EI
wpp = - M/B
wp = integrate(wpp,x) + C1
w =  integrate(wp,x) + C2
pprint("\nGeneral Solution:")
pprint("\nw:")
w = w.simplify()
tmp = w
pprint(w)

pprint("\nParticular solution:")
# Boundary Conditions:
# 1: w(a)  = 0
# 2: w'(a) = 0
bc1 = Eq(w.subs(x,a), 0)
bc2 = Eq(wp.subs(x,a), 0)

unknowns = [C1, C2]
eqns = [bc1, bc2]
sol = solve(eqns, unknowns)
sC1 = sol[C1]
sC2 = sol[C2]
pprint(sC1)
pprint(sC2)

pprint("\nw:")
w = w.subs({C1: sC1, C2: sC2})
w = w.simplify()
pprint(w)

pprint("\nw(x=0) / mm:")
w0 = w.subs(x, 0)
w0 = w0.subs(sub_list)
tmp = w0
tmp /= mm
tmp = iso_round(tmp,"0.01")
pprint(tmp)

pprint("\nw':")
wp = diff(w,x)
pprint(wp)

wp0 = wp.subs(x, 0)
wp0 = wp0.subs(sub_list)
psi = - wp0
pprint("\nψ(0):")
tmp = psi
pprint(tmp)
tmp = iso_round(tmp, "0.0001")
pprint(tmp)

pprint("\nψ(0) / °:")
tmp /= deg
tmp = iso_round(tmp, "0.0001")
pprint(tmp)

pprint("\nw(x = 3 m):")
tmp = w.subs(sub_list)
tmp = tmp.subs(x,3*m)
pprint(tmp)

pprint("\nw'(x = 3 m):")
tmp = wp.subs(sub_list)
tmp = tmp.subs(x,3*m)
pprint(tmp)

pprint("\n27 / 80:")
tmp = S(27)/80
tmp = iso_round(tmp, "0.01")
pprint(tmp)

EI / kNm²:
13000
  
M:
-x⋅(2⋅F + q⋅x) 
───────────────
       2       
                
M(x = 3 m)/ kNm:
-87/2
Integrating...
                 
General Solution:
  
w:
                     3      4
                  F⋅x    q⋅x 
E⋅I⋅(C₁⋅x + C₂) + ──── + ────
                   6      24 
─────────────────────────────
             E⋅I             
                    
Particular solution:
       2    3  
- 3⋅F⋅a  - a ⋅q
───────────────
     6⋅E⋅I     
     3      4  
8⋅F⋅a  + 3⋅a ⋅q
───────────────
     24⋅E⋅I    
  
w:
     3        3      4        2                    4
8⋅F⋅a  + 4⋅F⋅x  + 3⋅a ⋅q - 4⋅a ⋅x⋅(3⋅F + a⋅q) + q⋅x 
────────────────────────────────────────────────────
                       24⋅E⋅I                       
            
w(x=0) / mm:
9.26
   
w':
      2      2                    3
12⋅F⋅x  - 4⋅a ⋅(3⋅F + a⋅q) + 4⋅q⋅x 
───────────────────────────────────
               24⋅E⋅I              
     
ψ(0):
9/2000
0.0045
         
ψ(0) / °:
0.2578
           
w(x = 3 m):
0
            
w'(x = 3 m):
0
        
27 / 80:
0.34

Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.