3.3.A

Video

Simulation

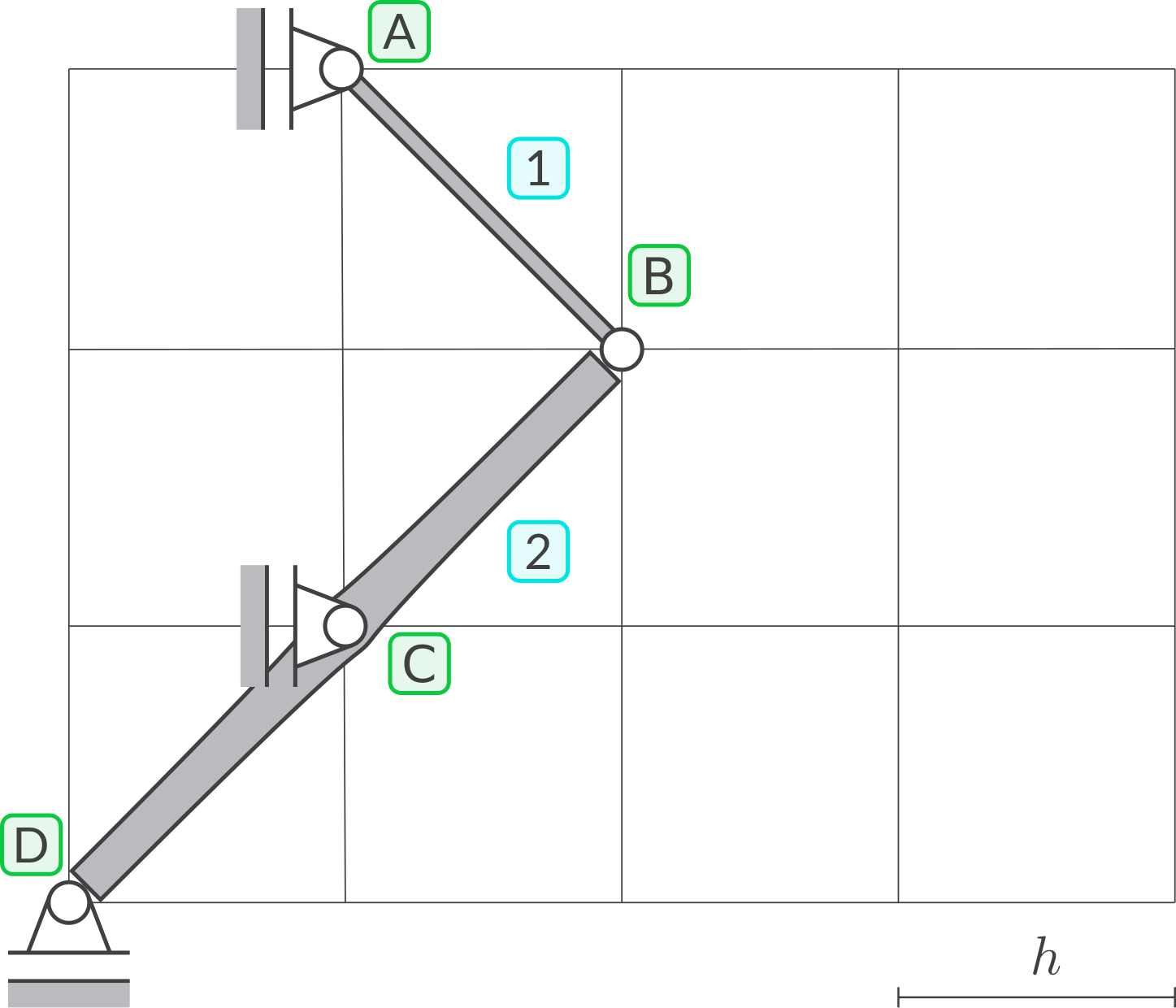
../../../_images/3.3.A.png

Gegebenes Symbol: \(h\)

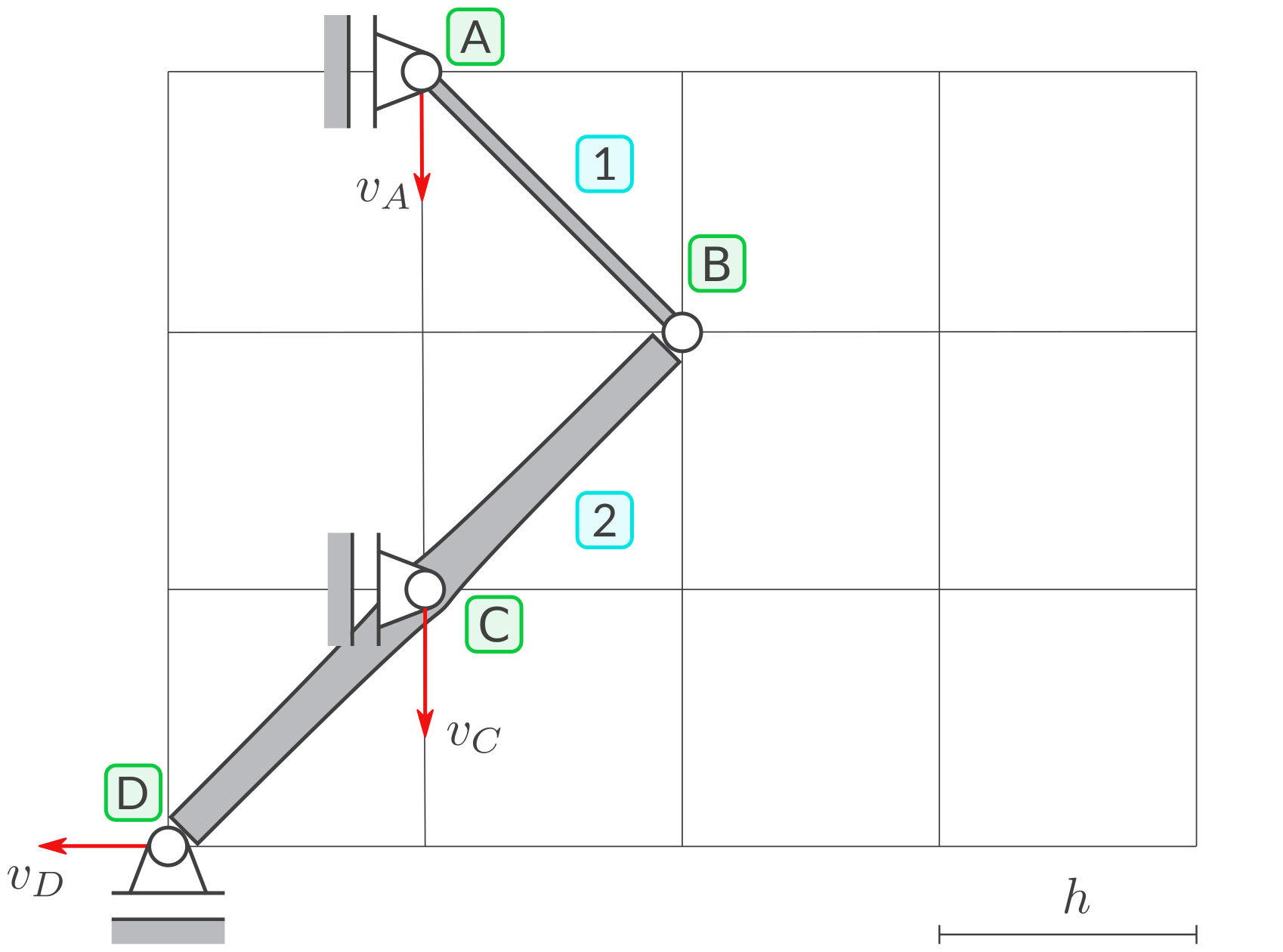
Es geht um ein bewegliches System, das aus den Starrkörpern 1 und 2 besteht. Im betrachteten Zeitpunkt ist das System in der dargestellten Lage.

  • Starrkörper 1 und 2 sind bei B gelenkig miteinander verbunden.

  • Das Gelenk A wird vertikal geführt.

  • Das Gelenk C wird vertikal geführt.

  • Das Gelenk D wird horizontal geführt.

1. Geschwindigkeiten von Teilchen

Definieren Sie mit Pfeilen:

  • \(v_A\): Die Geschwindigkeit eines Teilchens bei A (nach unten positiv).

  • \(v_C\): Die Geschwindigkeit eines Teilchens bei C (nach unten positiv).

  • \(v_D\): Die Geschwindigkeit eines Teilchens bei D (nach links positiv).

Lösung

../../../_images/3.3.A_1.png

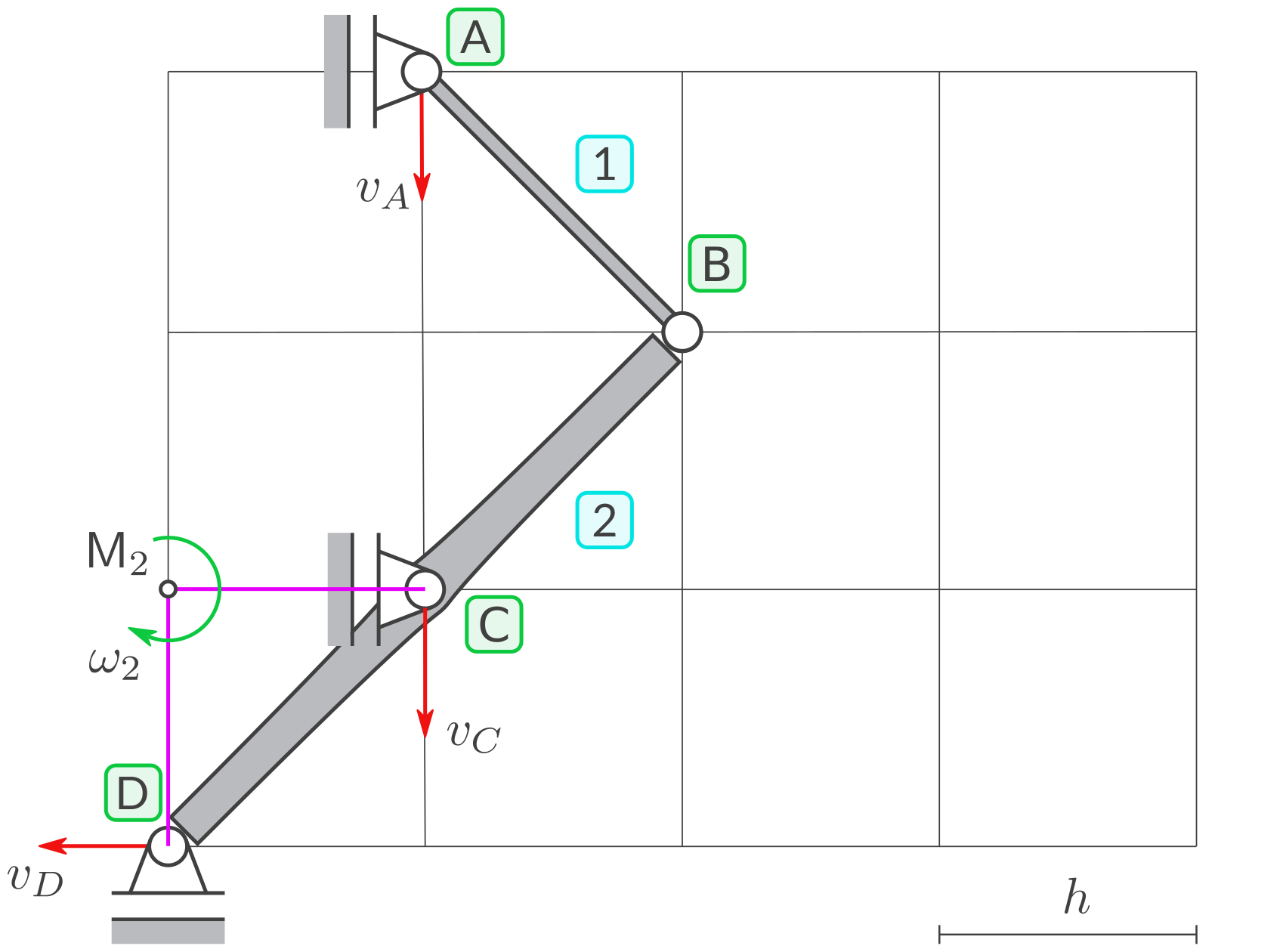
2. Winkelgeschwindigkeit von Körper 2

Definieren Sie die Winkelgeschwindigkeit \(\omega_2\) von Starrkörper 2 (positiv im Uhrzeigersinn). Und zwar am Momentanpol von Starrkörper 2.

Lösung

../../../_images/3.3.A_2.png

3.Winkelgeschwindigkeit von Körper 1

Definieren Sie die Winkelgeschwindigkeit \(\omega_1\) von Starrkörper 1 (positiv entgegen dem Uhrzeigersinn). Und zwar am Momentanpol von Starrkörper 1.

Lösung

../../../_images/3.3.A_3.png

4. Vergleich der Winkelgeschwindigkeiten

Zeigen Sie, dass:

\[\omega_1 = \omega_2\]

Lösung

../../../_images/3.3.A_3.png
\[\begin{split}v_B &= r \omega_1 \\ &= r \omega_2\end{split}\]

Darum ist:

\[\begin{split}r \omega_1 &= r \omega_2 \\\ \omega_1 &= \omega_2\end{split}\]

5. Geschwindigkeit von A

Zeigen Sie, dass:

\[v_A = 3 v_D\]

Lösung

../../../_images/3.3.A_3.png

D bewegt sich nach links, weil D unter dem Momentanpol liegt und Starrkörper 2 im Uhrzeigersinn rotiert. Da der Abstand zwischen \(\mathsf{M}_2\) und D ein Drittel des Abstands zwischen \(\mathsf{M}_1\) und A ist, und da beide Starrkörper dieselbe Winkelgeschwindigkeit \(\omega = \omega_1=\omega_2\) haben, gilt:

\[\begin{split}v_A&=3 h \omega \\ v_D&=h \omega\end{split}\]

Und darum ist:

\[v_A=3 v_D\]

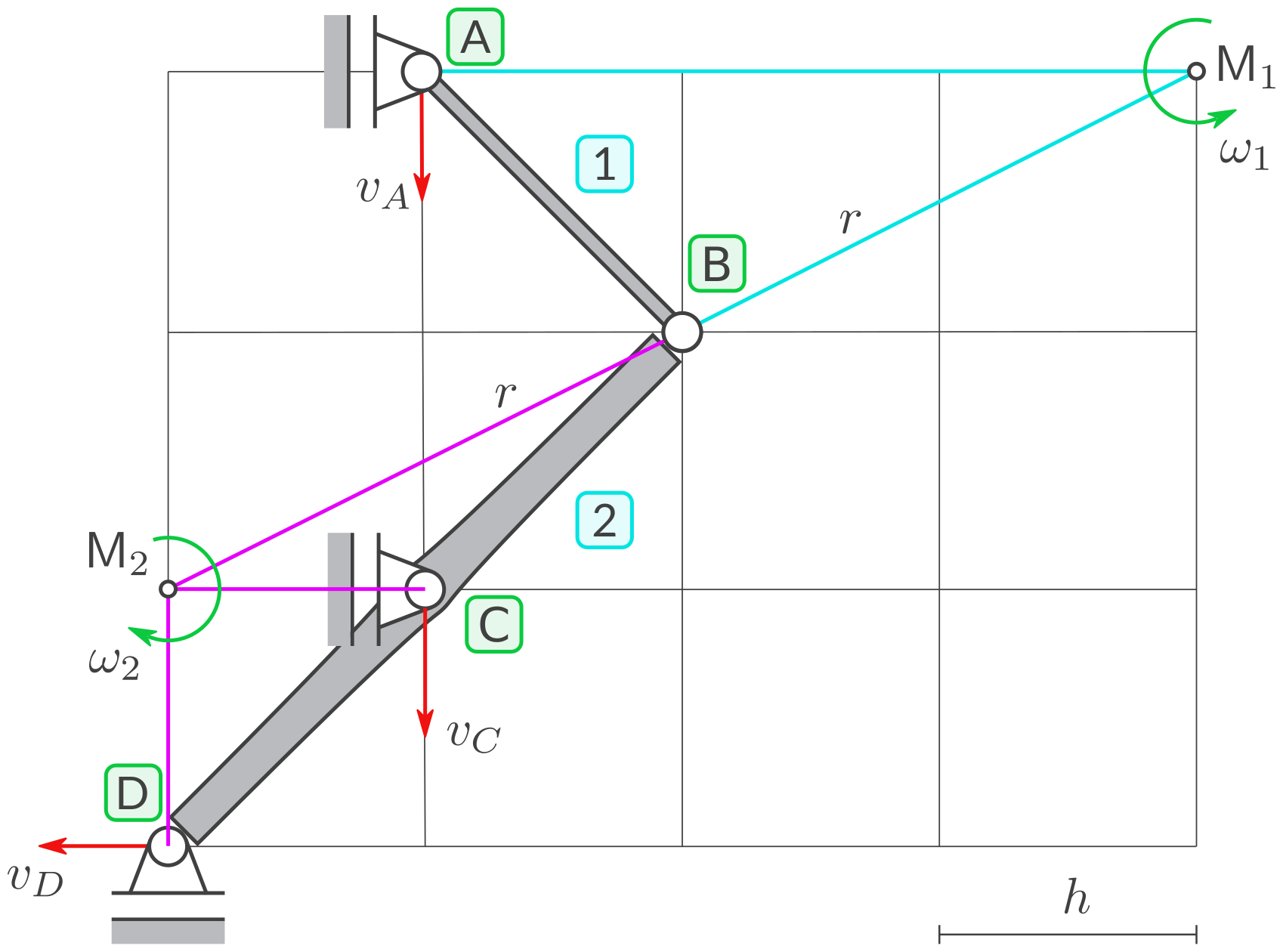
Berechnen Sie \(v_A\) für die folgenden gegebenen Größen:

\[\begin{split}v_D &= 2{,}5\,\tfrac{\mathrm m}{\mathrm s} \\ h &= 10\,\mathrm m\end{split}\]

Lösung

\[\begin{split}v_A &=3 v_D \\ &= 7{,}5\,\tfrac{\mathrm m}{\mathrm s}\end{split}\]

6. Winkelgeschwindigkeit von 2

Berechnen Sie die Winkelgeschwindigkeit \(\omega_2\) von Starrkörper 2 in \(\tfrac{1}{\mathrm s}\) (1 durch Sekunde) für dieselben gegebenen Größen.

Lösung

\[\begin{split}\omega_2 &= \tfrac{v_A}{3 h}\\ &= \tfrac{7.5\,\tfrac{\mathrm m}{\mathrm s}}{30\,\mathrm m} \\ &= 0{,}25 \,\tfrac{1}{\mathrm s}\end{split}\]