3.4.E
Gegeben
Symbole :
\[m, R, r, v_0, g \qquad \Theta = \tfrac25 m r^2\]
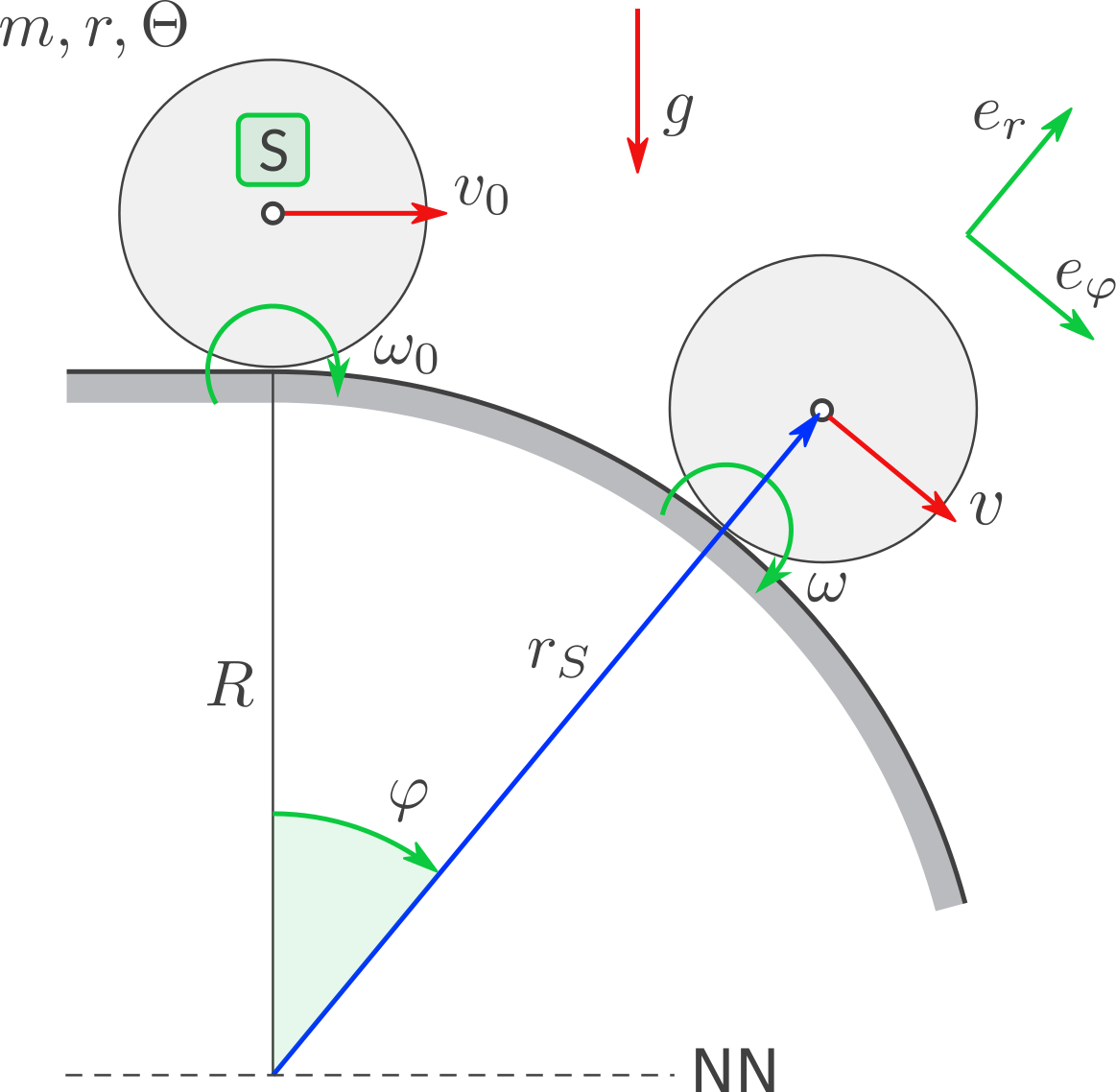
Eine Kugel mit Radius \(r\) und Masse \(m\) rollt im Schwerefeld auf einer Kreisbahn hinab.
Ihre Bewegung beginnt bei \(\varphi=0\) mit der Geschwindigkeit des Schwerpunkts \(v_0\) .
\(\Theta\) ist das Trägheitsmoment der Kugel bezüglich Schwerpunkt S.
a) Winkelgeschwindigkeit
Berechnen Sie für die gegebenen Symbole :
\[\omega_0 = \dots \quad,\quad \omega = \dots\]
Lösung
\[\begin{split}\omega_0 &= \tfrac{v_0}{r} \\
\omega &= \tfrac{v}{r}\end{split}\]
b) Energien
Berechnen Sie folgende Energien für die gegebenen Symbole :
\(E_0 = E_{\mathsf{kin},0} + E_{\mathsf{pot},0}\) : Energie der Kugel bei \(\varphi=0\) und Geschwindigkeit \(v_0\) .
\(E=E_{\mathsf{kin}} + E_{\mathsf{pot}}\) : Energie bei beliebigem Winkel \(\varphi\) und Geschwindigkeit \(v\) .
Lösung
\[\begin{split}E_{\mathsf{kin},0} &= \tfrac{1}{2} m {v_0}^2 + \tfrac{1}{2} \Theta {\omega_0}^2 \\
E_{\mathsf{pot},0} &= mg(R+r) \\
E_{\mathsf{kin}} &= \tfrac{1}{2} m v^2 + \tfrac{1}{2} \Theta \omega^2 \\
E_{\mathsf{pot}} &= mg(R+r)\cos{\varphi}\end{split}\]
c) Energiesatz
Berechnen Sie mit dem Energiesatz die Geschwindigkeit \(v\) bzw. \(v^2\) abhängig von \(\varphi\) und abhängig von den gegebenen Symbolen .
\[v^2(\varphi) = \dots\]
Lösung
Energiesatz:
\[\begin{split}E_0 &= E \\
E_{\mathsf{kin},0} + E_{\mathsf{pot},0} &= E_{\mathsf{kin}} + E_{\mathsf{pot}} \\
\tfrac{1}{2} m {v_0}^2 + \tfrac{1}{2} \Theta {\omega_0}^2 + mg(R+r) &=
\tfrac{1}{2} m v^2 + \tfrac{1}{2} \Theta \omega^2 + mg(R+r)\cos{\varphi}\end{split}\]
Einsetzen vom gegebenen \(\Theta = \tfrac25 m r^2\) sowie Einsetzen von \(\omega_0 = \tfrac{v_0}{r}\) und \(\omega = \tfrac{v}{r}\) liefert:
\[v^2 = {v_0}^2 + \tfrac{10}{7}g(R+r)(1- \cos{\varphi})\]
Details
\[m {v_0}^2 + \Theta {\omega_0}^2 =
m v^2 + \Theta \omega^2 + 2 mg(R+r) \left( \cos{\varphi} - 1 \right)\]
Einsetzen vom gegebenen \(\Theta = \tfrac25 m r^2\) liefert:
\[\begin{split}m {v_0}^2 + \tfrac25 m r^2 {\omega_0}^2 &=
m v^2 + \tfrac25 m r^2 \omega^2 + 2 mg(R+r) \left( \cos{\varphi} - 1 \right) \\
{v_0}^2 + \tfrac25 r^2 {\omega_0}^2 &=
v^2 + \tfrac25 r^2 \omega^2 + 2 g(R+r) \left( \cos{\varphi} - 1 \right)\end{split}\]
Einsetzen von \(\omega_0 = \tfrac{v_0}{r}\) und \(\omega = \tfrac{v}{r}\) liefert:
\[\begin{split}{v_0}^2 + \tfrac25 r^2 \frac{v_0^2}{r^2} &=
v^2 + \tfrac25 r^2 \frac{v^2}{r^2} + 2 g(R+r) \left( \cos{\varphi} - 1 \right) \\
{v_0}^2 + \tfrac25 v_0^2 &=
v^2 + \tfrac25 v^2 + 2 g(R+r) \left( \cos{\varphi} - 1 \right) \\
5 {v_0}^2 + 2 v_0^2 &=
5 v^2 + 2 v^2 + 10 g(R+r) \left( \cos{\varphi} - 1 \right) \\
7 {v_0}^2 &=
7 v^2 + 10 g(R+r) \left( \cos{\varphi} - 1 \right) \\
{v_0}^2 &=
v^2 + \tfrac{10}{7} g(R+r) \left( \cos{\varphi} - 1 \right) \\
{v_0}^2 &=
v^2 - \tfrac{10}{7} g(R+r) \left( 1 - \cos{\varphi} \right) \\\end{split}\]
Ergebnis:
\[v^2 = {v_0}^2 + \tfrac{10}{7}g(R+r)(1- \cos{\varphi})\]
d) Schwerpunkt-Beschleunigung
Der Ortsvektor zum Schwerpunkt ist:
\[\boldsymbol{r_S} = (R+r) \boldsymbol e_R\]
Zeigen Sie, dass die Beschleunigung des Schwerpunkts ist:
\[\boldsymbol a =
- (R+r) \dot{\varphi}^2 \boldsymbol e_R
+ (R+r) \ddot \varphi \boldsymbol e_\varphi\]
Lösung
Beschleunigung des Schwerpunkts, der sich auf einer Kreisbahn mit Radius \(R+r\) bewegt:
\[\begin{split}\boldsymbol{r_S} &= (R+r) \boldsymbol e_R\\
\boldsymbol{v} &= (R+r) \dot{\varphi} \boldsymbol e_\varphi \\
\boldsymbol a &= \underbrace{-(R+r) \dot{\varphi}^2}_{a_R} \boldsymbol e_R +
\underbrace{(R+r) \ddot \varphi}_{a_\varphi} \boldsymbol e_\varphi\end{split}\]
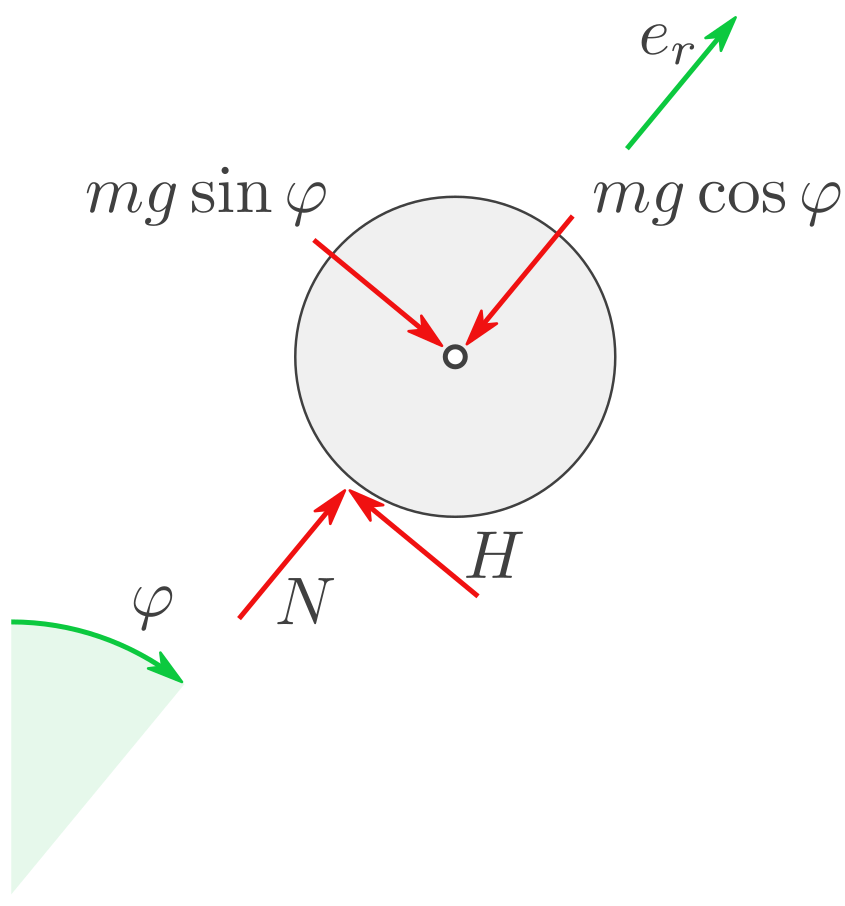
e) Normalkraft
Betrachten Sie ab hier den Fall, dass die Anfangsgeschwindigkeit Null ist, also \(v_0=0\) .
Schneiden Sie die Kugel frei. Und berechnen Sie die Normalkraft \(N\) zwischen Kugel und Kreisbahn abhängig von \(\varphi\) - mit dem Schwerpunktsatz und für die gegebenen Symbole . Zeigen Sie, dass:
\[N = mg\left(\tfrac{17}{7} \cos{\varphi} - \tfrac{10}{7}\right)\]
Berechnen Sie \(N\) in \(\mathrm{N}\) (Newton) gerundet auf Rundestellenwert \(0{,}1\) für \(\varphi=45^\circ\) und für die Größen :
\[m = 5\,\mathrm{kg}\quad,\quad g = 9{,}81 \,\tfrac{\mathrm{m}}{\mathrm s^2}\]
Lösung
Die Beschleunigung des Schwerpunkts in \(\boldsymbol e_R\) -Richtung ist:
\[\begin{split}a_R
&= -(R+r) \dot{\varphi}^2 \\
&= -(R+r) \tfrac{v^2}{(R+r)^2} \\
&= - \tfrac{v^2}{R+r}\end{split}\]
Einsetzen dieser Beschleunigung in den Schwerpunktsatz in \(\boldsymbol e_R\) -Richtung:
\[\begin{split}ma_R &= N - mg \cos{\varphi}\\
-m \tfrac{v^2}{R+r} &= N - mg \cos{\varphi}\\
N &= mg \cos{\varphi} -m \tfrac{v^2}{R+r}\end{split}\]
Einsetzen von \(v^2\) wie oben berechnet sowie \(v_0=0\) ergibt:
\[\begin{split}N
&= mg\left( \cos{\varphi} - \tfrac{10}{7}(1- \cos{\varphi})\right)\\
&= mg\left(\tfrac{17}{7} \cos{\varphi} - \tfrac{10}{7}\right)\end{split}\]
Einsetzen von \(\varphi=45^\circ\) und den gegebenen Größen ergibt:
\[N \stackrel{\scriptscriptstyle{0{,}1}}{\approx} 14{,}2\,\mathrm{N}\]
f) Abhebe-Winkel
Berechnen Sie den Winkel \(\varphi^*\) , für den die Kugel abhebt, in \(^\circ\) (Grad) und gerundet auf Rundestellenwert \(0{,}1\) :
\[\varphi^*\stackrel{\scriptscriptstyle{0{,}1}}{\approx} \dots^\circ\]
Lösung
Die Kugel hebt ab für \(N=0\) , sodass:
\[\begin{split}\tfrac{17}{7} \cos{\varphi^*} - \tfrac{10}{7}&= 0\\
\cos \varphi^* - \tfrac{10}{17}&=0\\
\varphi^* &\stackrel{\scriptscriptstyle{0{,}1}}{\approx} 54{,}0^\circ\end{split}\]
Bokeh Plot
