A.2.4 Mohrscher Kreis
Bemerkung
Videos siehe A.0.8 Tensor-Komponenten
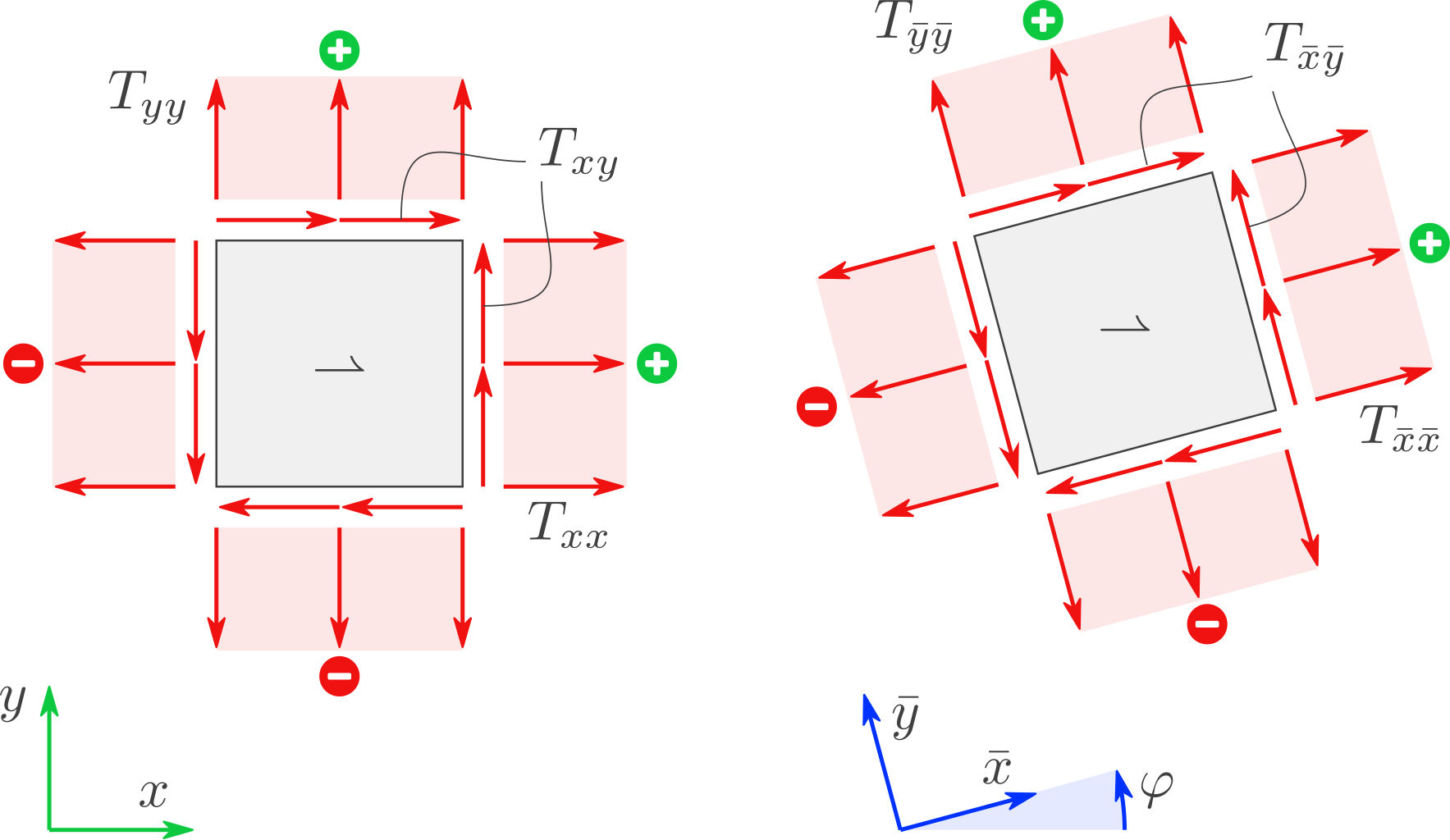
Scheibe unter Spannung. Fasern des Materials sind rot markiert, damit man sieht, wie das Material liegt. Links und rechts liegt das Material also gleich. Nur ist die Scheibe unterschiedlich ausgeschnitten.
Gegeben
Die zwei Bezugssysteme \((x, y)\) und \((\bar x,\bar y)\).
Die dimensionslosen \((x,y)\)-Komponenten eines symmetrischen Tensors in 2D, zum Beispiel des Spannungstensors:
\[\begin{split}\begin{bmatrix} T_{xx} & T_{xy} \\ \mathsf{sym} & T_{yy} \end{bmatrix} = \begin{bmatrix} -1 & 4 \\ \mathsf{sym} & 5 \end{bmatrix}\end{split}\]Die Formeln aus Passive Transformation.
Gesucht
Der Kreis, aus dem man verschiedene Größen ablesen kann.
Die Komponenten \((T_{\bar x\bar x}, T_{\bar x \bar y})\) für beliebige Winkel \(\varphi\).
Die Extremwerte:
Das maximale und minimale \(T_{\bar x\bar x}\) sowie die zugehörigen Winkel.
Das maximale und minimale \(T_{\bar x\bar y}\) sowie die zugehörigen Winkel.
a) Kreis
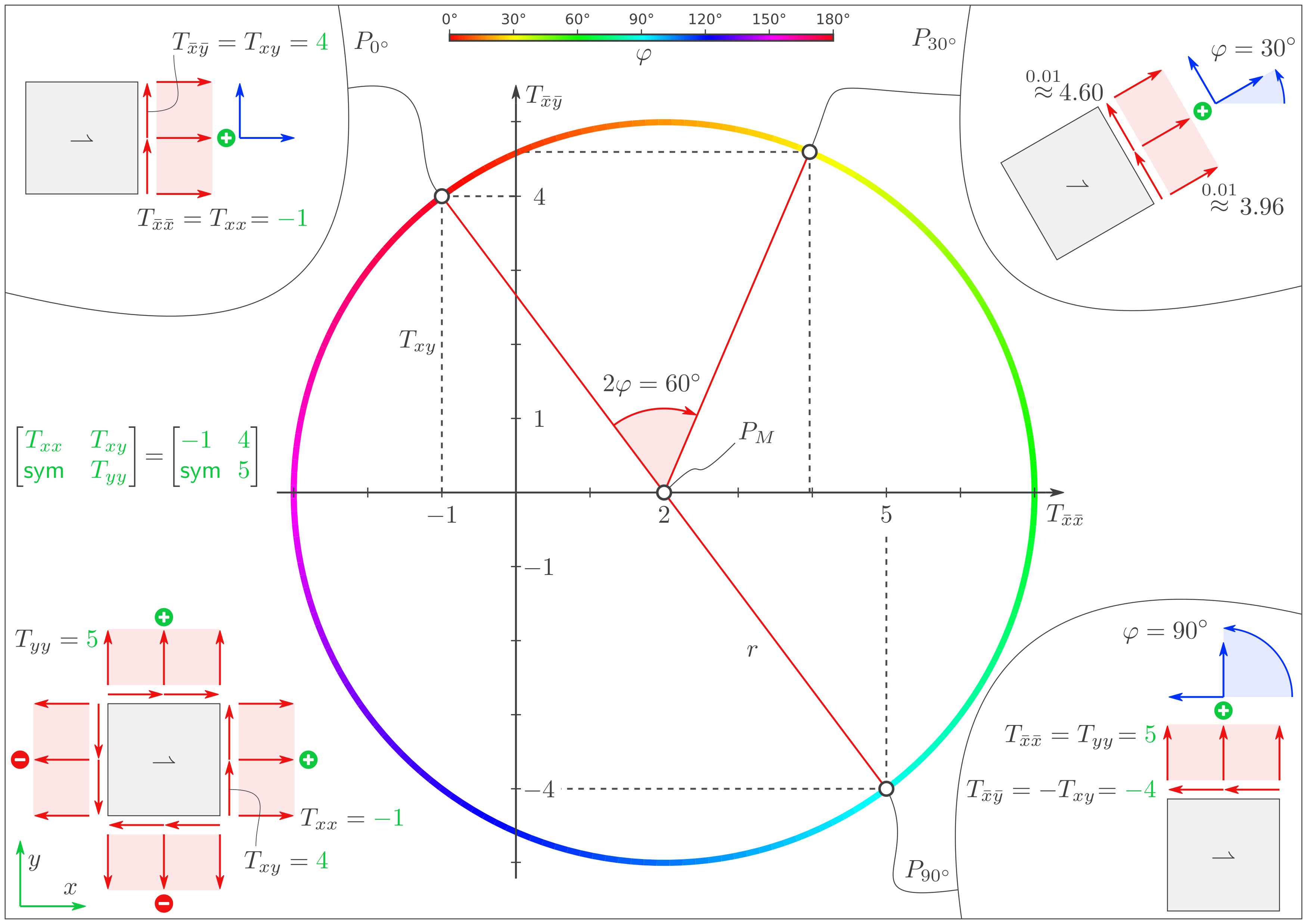
Horizontale Achse: \(T_{\bar x \bar x}\) Vertikale Achse: \(T_{\bar x \bar y}\)1. Zeichnen der Diagramm-Achsen
Punkt Komponenten Beispiel Position \(P_{0^\circ}\) \((T_{xx}, T_{xy})\) \((-1, 4)\) auf dem Kreis \(P_{90^\circ}\) \((T_{yy}, -T_{xy})\) \((5, -4)\) gegenüber \(P_{0^\circ}\) \(P_{M}\) \((\bar{T}, 0)\) \((2,0)\) Kreismittelpunkt mit \(\bar{T} = \tfrac12 \left(T_{xx} + T_{yy}\right)\).2. Zeichnen des Kreises aus 3 Punkten
Punkt Komponenten Beispiel Position \(P_{\varphi_1}\) \((\bar{T} + r, 0)\) \(( 7 , 0 )\) 3 Uhr \(P_{\varphi_1+90^\circ}\) \((\bar{T} - r, 0)\) \((-3 , 0 )\) 9 Uhr \(P_{\varphi_1-45^\circ}\) \((\bar{T}, 0 + r)\) \(( 2 , 5 )\) 12 Uhr \(P_{\varphi_1+45^\circ}\) \((\bar{T}, 0 - r)\) \(( 2 , -5 )\) 6 Uhr mit \(\tilde T = \tfrac12 \left(T_{xx}-T_{yy}\right)\) und \(r = \sqrt{{\tilde T}^2 +T_{xy}^2}\).3. Zeichnen von weiteren 4 Punkten
b) Komponenten

Roten Radius zeichnen zwischen \(P_{M}\) und \(P_{0^\circ}\). Roten Winkel \(2\varphi\) zeichnen. Neuen Radius und neuen Punkt auf den Kreis zeichnen. Punktkoordinaten \((T_{\bar x\bar x}, T_{\bar x \bar y})\) ablesen. Beispiel Punkt Komponenten \(\varphi\) (blau) \(2 \varphi\) (rot) \(P_{0^\circ}\) \((-1, 4)\) \(0^\circ\) \(0^\circ\) \(P_{30^\circ}\) \((3{,}96, \, 4{,}60)\) \(30^\circ\) \(60^\circ\) \(P_{60^\circ}\) \((6{,}96, \, 0{,}60)\) \(60^\circ\) \(120^\circ\) \(P_{90^\circ}\) \((5, -4)\) \(90^\circ\) \(180^\circ\)Ablesen der Komponenten
c) Extremwerte
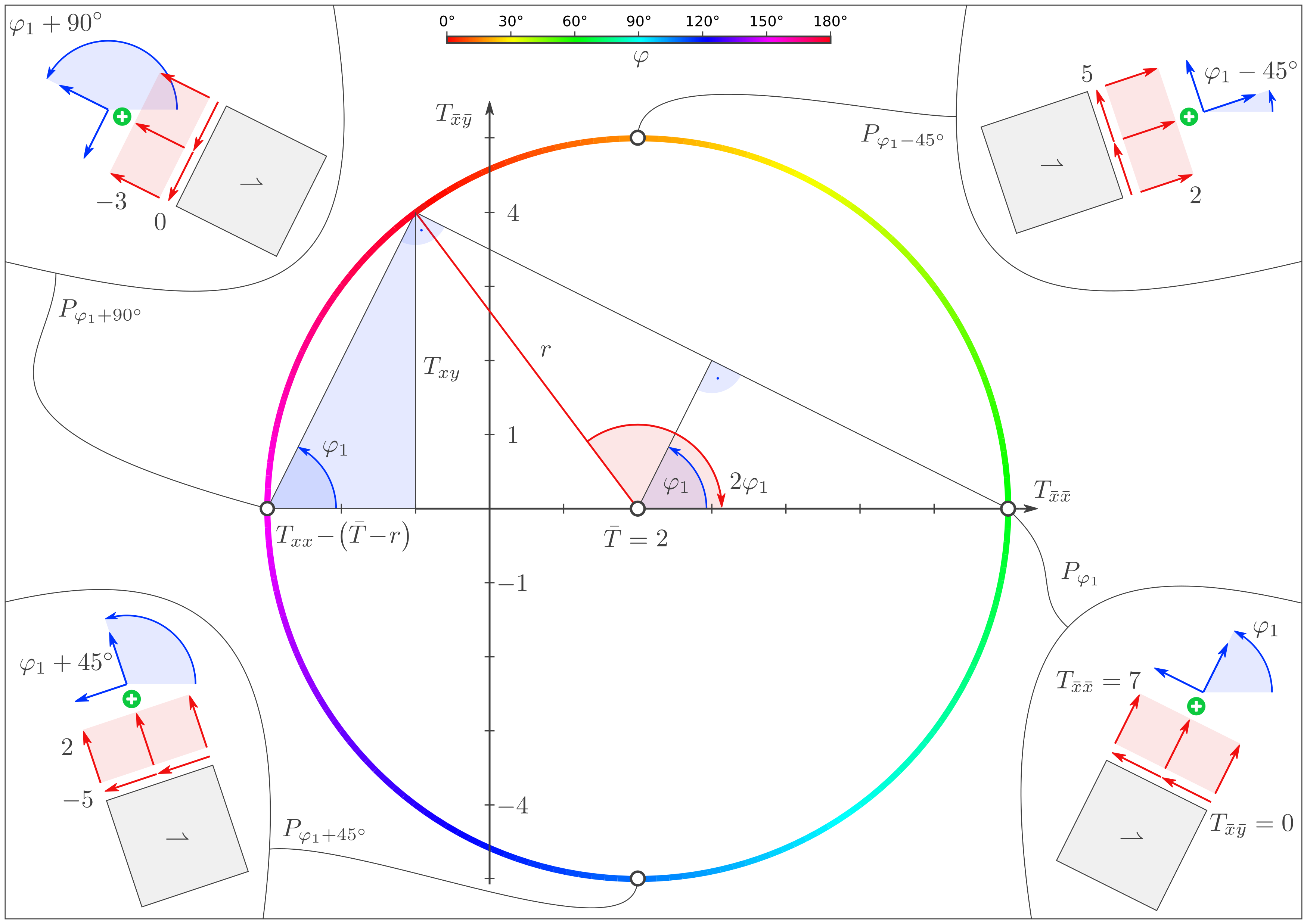
Punkt Komponenten Extremwert Winkel Def.-Bereich \(P_{\varphi_1}\) \((\max T_{\bar x \bar x} ,0)\) \(\max T_{\bar x \bar x}=\bar T + r\) \(\varphi_1\) \((-90^\circ, 90^\circ]\) \(P_{\varphi_1 + 90^\circ}\) \((\min T_{\bar x \bar x} ,0)\) \(\min T_{\bar x \bar x}=\bar T - r\) \(\varphi_1 \!+\! 90^\circ\) \((0^\circ, 180^\circ]\) \(P_{\varphi_1-45^\circ}\) \((\bar T, \max T_{\bar x \bar y})\) \(\max T_{\bar x \bar y}= r\) \(\varphi_1 \!-\! 45^\circ\) \((-135^\circ, 45^\circ]\) \(P_{\varphi_1+45^\circ}\) \((\bar T, \min T_{\bar x \bar y})\) \(\min T_{\bar x \bar y}= -r\) \(\varphi_1 \!+\! 45^\circ\) \((-45^\circ, 135^\circ]\) mit \(\varphi_1 =\arctan{} \tfrac{T_{xy}}{r + \tilde T}\). Merkzettel: Winkel, für den \(T_{\bar x \bar x}\) maximal ist mit \(\varphi_1 \in (-90^\circ, 90^\circ]\) Beispiel Punkt Komponenten Extremwert Winkel (gerundet auf 1 Grad) \(P_{\varphi_1}\) \((7,0)\) \(\max T_{\bar x \bar x}= 7\) \(63^\circ\) \(P_{\varphi_1+90^\circ}\) \((-3,0)\) \(\min T_{\bar x \bar x}= -3\) \(153^\circ\) \(P_{\varphi_1-45^\circ}\) \((2, 5)\) \(\max T_{\bar x \bar y}= 5\) \(18^\circ\) \(P_{\varphi_1+45^\circ}\) \((2, -5)\) \(\min T_{\bar x \bar y}= -5\) \(108^\circ\)Ablesen der Extremwerte und der zugehörigen Winkel