B2.E
Video
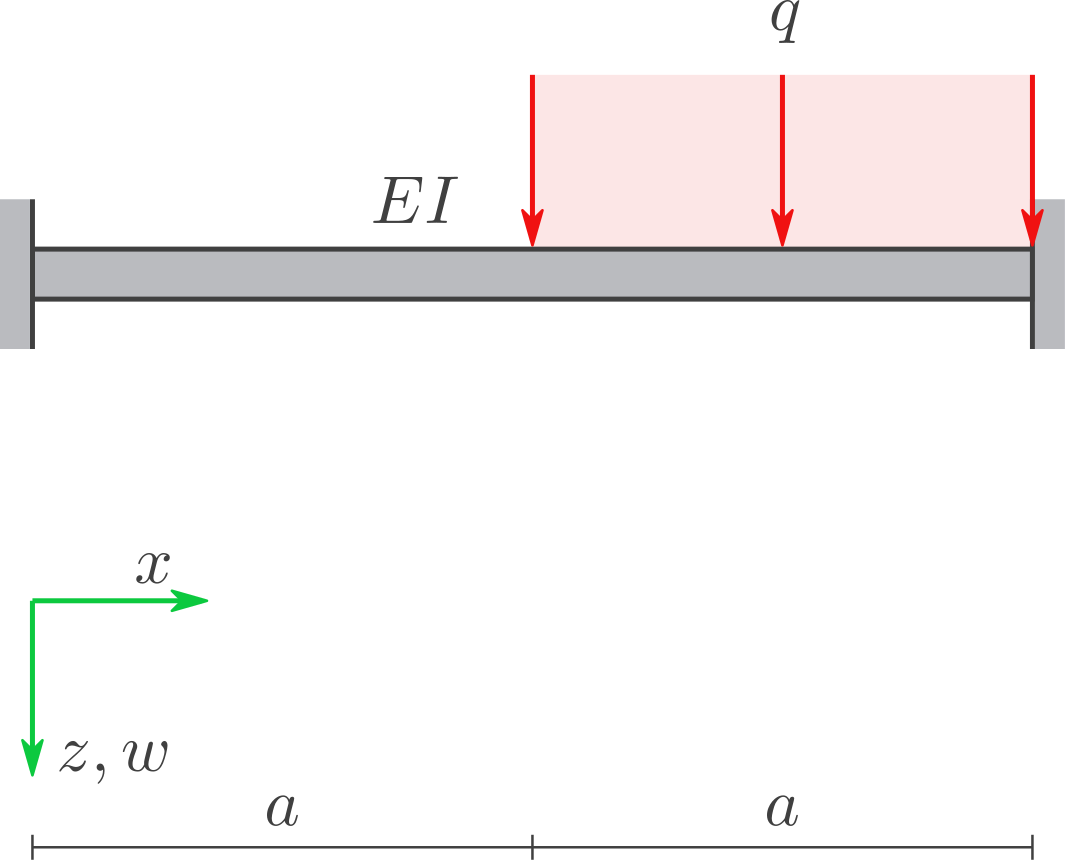
Gegebene Symbole: \(a, q, EI\)
Gegeben ist ein Balken mit Elastizitätsmodul \(E\) und Flächenträgheitsmoment \(I\).
Untersuchen Sie die Struktur:
mit zwei Finiten Elementen. Und untersuchen Sie die Struktur danach noch einmal
mit einem Finiten Element - und unter Ausnutzung von Symmetrien.
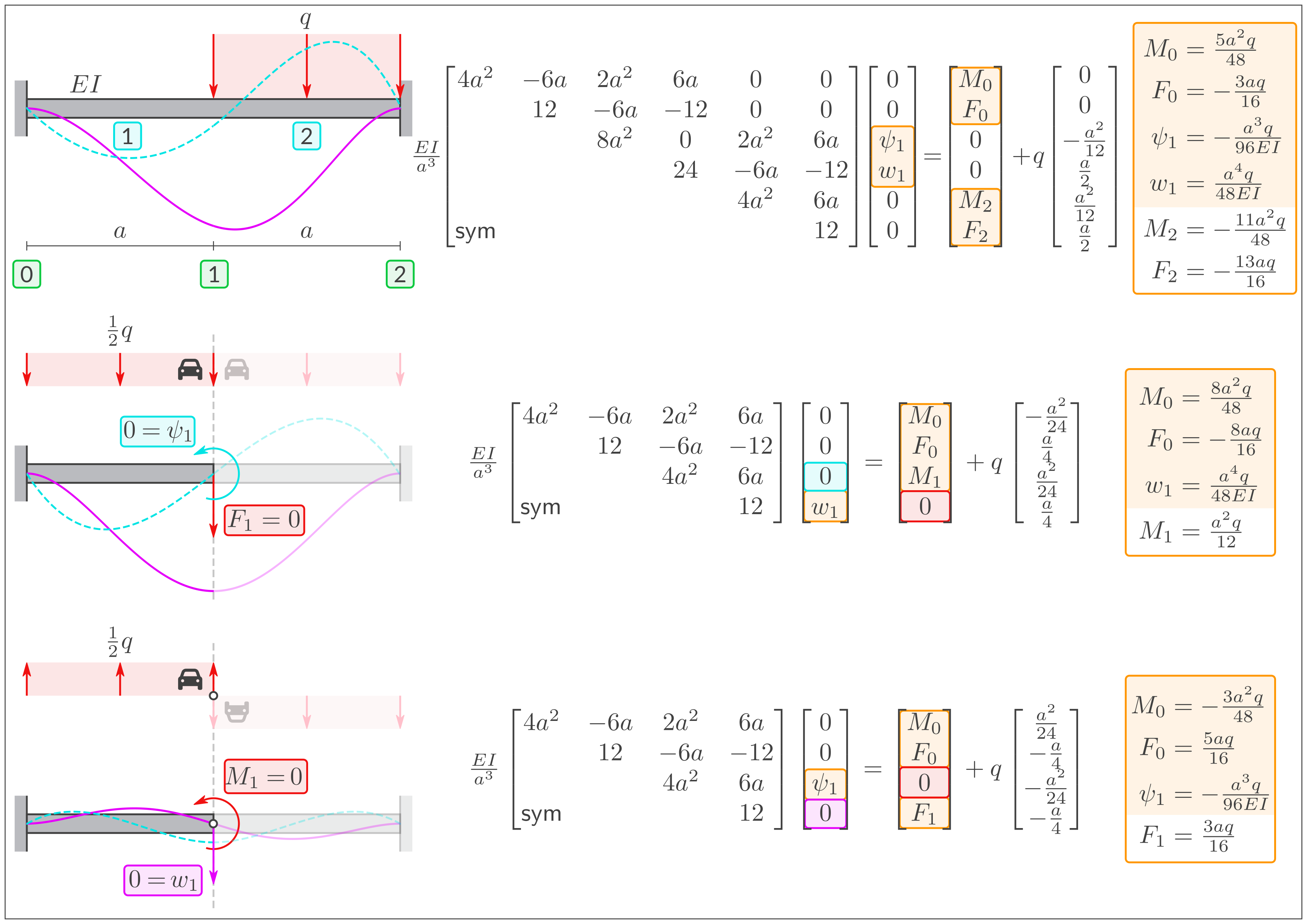
Oben: 2 Elemente ohne Symmetrieausnutzung. Mitte: Die lila \(w\)-Funktion ist achsensymmetrisch, so dass \(\psi_1 = F_1=0.\) Unten: Die lila \(w\)-Funktion ist punktsymmetrisch, so dass \(w_1 = M_1=0.\) \(w\) \(\psi = - w'\) \(M = - EI w''\) \(Q = -EI w'''\) Daraus ergeben sich folgende Werte auf dem Symmetrielinie: \(w\) ist punktsymmetrisch \(\leadsto w_1 = 0\) \(\psi\) ist achsensymmetrisch \(\leadsto \psi_1 = 0\) \(M\) ist punktsymmetrisch \(\leadsto M_1 = 0\) \(Q\) ist achsensymmetrisch \(\leadsto F_1 = 0\)Lösung
Details
Balken-Aufgaben in SymPy gelöst
Lösung einiger Balken-Aufgaben in einem Programm hier.

