M.2.B
Bemerkung
Grundlagen und Videos: A.0.7 Vektor-Komponenten

Gegeben:
Das grüne \((x,y)\)-Bezugssystem und das blaue \((\bar x, \bar y)\)-Bezugssystem.
Der Winkel \(\varphi=10^\circ\), um den das blaue Bezugssystem relativ zum grünen Bezugssystem gedreht ist.
Die Komponenten des roten Vektors \(\boldsymbol v\) im grünen Bezugssystem:
\[\begin{split}\begin{bmatrix} v_x \\ v_y \end{bmatrix} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}\end{split}\]
Gesucht:
Die Komponenten des Vektors im blauen Bezugssystem:
a) Kosinus und Sinus
Berechnen Sie Kosinus und Sinus des gegebenen Winkels \(\varphi=10^\circ\) - und zwar gerundet auf \(0{,}01\):
Lösung
b) Drehmatrix
Passive Transformation:
Berechnen Sie die vier Einträge der Drehmatrix \(R_\varphi,\) und zwar gerundet auf \(0{,}01\):
Lösung
c) Komponenten im gedrehten Bezugssystem
Berechnen Sie gerundet auf \(0{,}01\):
Zeigen Sie an einer Skizze, dass das Ergebnis plausibel ist.
Plausibilitätskontrolle: Die beiden Bezugssysteme zeichnen. Den Vektor zeichnen. Die Komponenten ablesen.Lösung
e) Infinitesimale Drehung

Die Komponenten im gedrehten Bezugssystem sind (abhängig von \(\varphi\)):
Für betragsmäßig kleine Winkel \(\varphi\) gilt: \(c_\varphi\approx 1\) und \(s_\varphi\approx \varphi\). Falls das \((\bar x, \bar y)\)-Bezugssystem nur sehr wenig (infinitesimal) relativ zum \((x, y)\)-Bezugssystem gedreht ist, gilt daher näherungsweise:
Füllen Sie folgende Tabelle mit Werten gerundet auf Rundestellenwert \(0{,}0001\).
\(\varphi\) |
\(R_\varphi=\begin{bmatrix} c_\varphi & s_\varphi \\ -s_\varphi & c_\varphi \end{bmatrix}\) |
\(\tilde R_\varphi=\begin{bmatrix} 1 & \varphi \\ -\varphi & 1 \end{bmatrix}\) |
\(R_\varphi \begin{bmatrix} 3 \\ 4 \end{bmatrix}\) |
\(\tilde R_\varphi \begin{bmatrix} 3 \\ 4 \end{bmatrix}\) |
\(1^\circ\) |
\(\begin{bmatrix}0{,}9998 & 0{,}0175\\-0{,}0175 & 0{,}9998\end{bmatrix}\) |
\(\ldots\) |
\(\begin{bmatrix}3{,}0694\\3{,}947\end{bmatrix}\) |
\(\ldots\) |
\(3^\circ\) |
\(\ldots\) |
\(\ldots\) |
\(\ldots\) |
\(\ldots\) |
\(-3^\circ\) |
\(\ldots\) |
\(\ldots\) |
\(\ldots\) |
\(\ldots\) |
\(5^\circ\) |
\(\ldots\) |
\(\ldots\) |
\(\ldots\) |
\(\ldots\) |
\(\varphi\) \(R_\varphi=\begin{bmatrix} c_\varphi & s_\varphi \\ -s_\varphi & c_\varphi \end{bmatrix}\) \(\tilde R_\varphi=\begin{bmatrix} 1 & \varphi \\ -\varphi & 1 \end{bmatrix}\) \(R_\varphi \begin{bmatrix} 3 \\ 4 \end{bmatrix}\) \(\tilde R_\varphi \begin{bmatrix} 3 \\ 4 \end{bmatrix}\) \(1^\circ\) \(\begin{bmatrix}0{,}9998 & 0{,}0175\\-0{,}0175 & 0{,}9998\end{bmatrix}\) \(\begin{bmatrix}1{,}0 & 0{,}0175\\-0{,}0175 & 1{,}0\end{bmatrix}\) \(\begin{bmatrix}3{,}0694\\3{,}947\end{bmatrix}\) \(\begin{bmatrix}3{,}0698\\3{,}9476\end{bmatrix}\) \(3^\circ\) \(\begin{bmatrix}0{,}9986 & 0{,}0523\\-0{,}0523 & 0{,}9986\end{bmatrix}\) \(\begin{bmatrix}1{,}0 & 0{,}0524\\-0{,}0524 & 1{,}0\end{bmatrix}\) \(\begin{bmatrix}3{,}2052\\3{,}8375\end{bmatrix}\) \(\begin{bmatrix}3{,}2094\\3{,}8429\end{bmatrix}\) \(-3^\circ\) \(\begin{bmatrix}0{,}9986 & -0{,}0523\\0{,}0523 & 0{,}9986\end{bmatrix}\) \(\begin{bmatrix}1{,}0 & -0{,}0524\\0{,}0524 & 1{,}0\end{bmatrix}\) \(\begin{bmatrix}2{,}7865\\4{,}1515\end{bmatrix}\) \(\begin{bmatrix}2{,}7906\\4{,}1571\end{bmatrix}\) \(5^\circ\) \(\begin{bmatrix}0{,}9962 & 0{,}0872\\-0{,}0872 & 0{,}9962\end{bmatrix}\) \(\begin{bmatrix}1{,}0 & 0{,}0873\\-0{,}0873 & 1{,}0\end{bmatrix}\) \(\begin{bmatrix}3{,}3372\\3{,}7233\end{bmatrix}\) \(\begin{bmatrix}3{,}3491\\3{,}7382\end{bmatrix}\)Lösung
f) Web-App
\((v_{\bar x} , v_{\bar x})\) für einen gegebenen Winkel \(\varphi\) am Kreis ablesen: Ganzzahliges Vielfaches von \(360^\circ\) zu \(\varphi\) addieren, so dass \(\varphi\) zwischen \(-180^\circ \le \varphi \le 180^\circ\) Diesen Winkel \(\varphi\) am Schieberegler einstellen, und zwar in \(^\circ\) (Grad). \((v_{\bar x} , v_{\bar x})\) am Kreis ablesen als die Koordinaten des Punkts auf dem Kreis. Beispiele: \(\varphi\) Bezugssystem-Drehung \(\varphi / \mathrm{deg}\) auf Schieberegler \(10^\circ\) 10 Grad gegen Uhrzeigersinn 10 \(-10^\circ\) 10 Grad im Uhrzeigersinn -10 \(370^\circ\) 370 Grad gegen Uhrzeigersinn 10 \(190^\circ\) 190 Grad gegen Uhrzeigersinn -170Anleitung
g) Weitere Beispiele
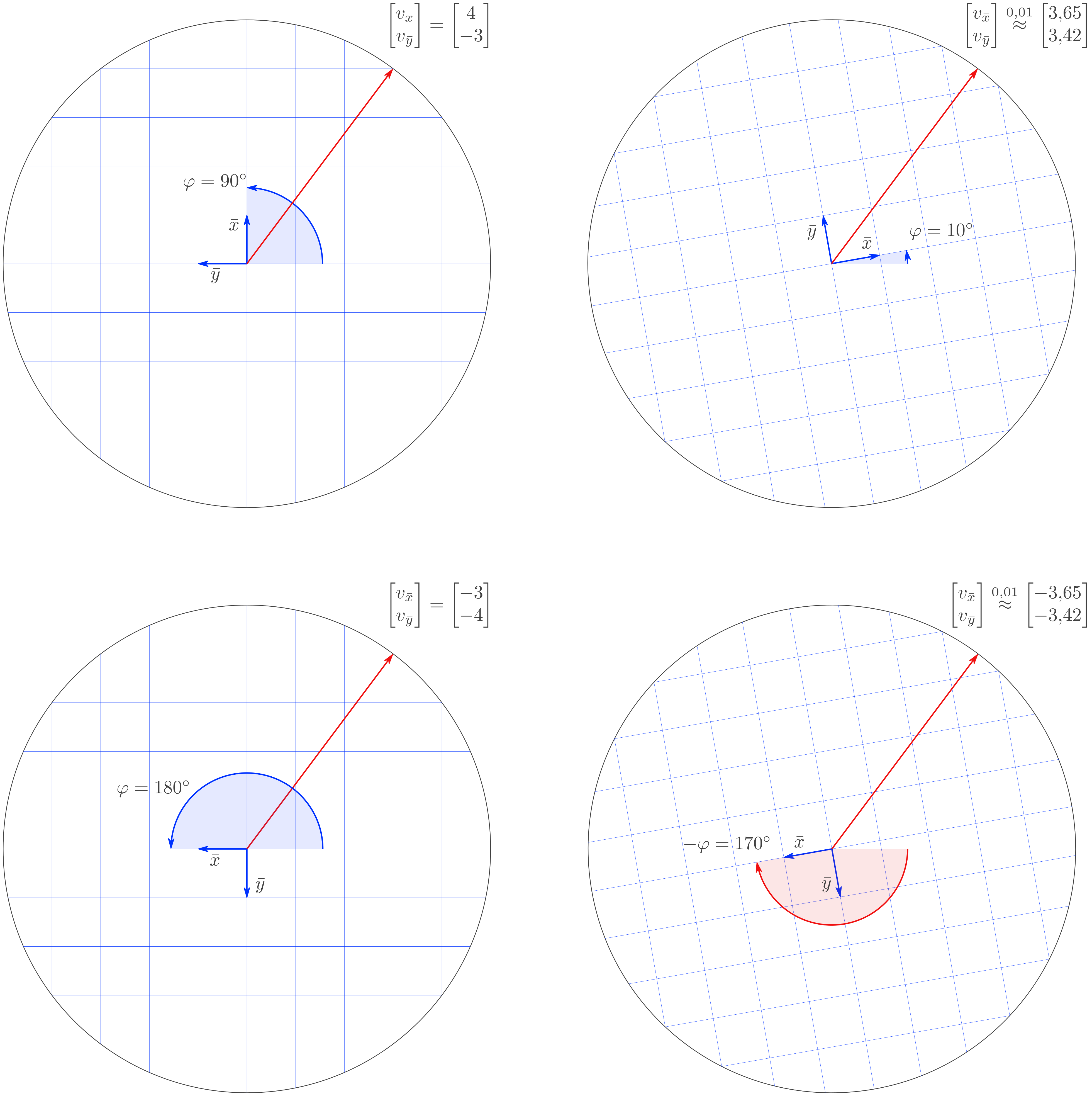
\(\varphi\) |
\(\begin{bmatrix} c_\varphi & s_\varphi \\ -s_\varphi & c_\varphi \end{bmatrix}\) |
\(\begin{bmatrix} v_{\bar x} \\ v_{\bar y} \end{bmatrix}\) |
\(10^\circ\) |
\(\begin{bmatrix} 0{,}98 & 0{,}17 \\ -0{,}17 & 0{,}98 \end{bmatrix}\) |
\(\begin{bmatrix} 3{,}65\\ 3{,}42 \end{bmatrix}\) |
\(90^\circ\) |
\(\begin{bmatrix} 0{,}0 & 1{,}0 \\ -1{,}0 & 0{,}0 \end{bmatrix}\) |
\(\begin{bmatrix} 4{,}0 \\ -3{,}0 \end{bmatrix}\) |
\(180^\circ\) |
\(\begin{bmatrix} -1{,}0 & 0{,}0 \\ 0{,}0 & -1{,}0 \end{bmatrix}\) |
\(\begin{bmatrix} -3{,}0 \\ -4{,}0 \end{bmatrix}\) |
\(-170^\circ\) |
\(\begin{bmatrix} -0{,}98 & -0{,}17 \\ 0{,}17 & -0{,}98 \end{bmatrix}\) |
\(\begin{bmatrix} -3{,}65 \\ -3{,}42 \end{bmatrix}\) |
Anstatt \(5\,\mathrm{m}\) (Meter) nach hinten zu gehen, kann man gleichbedeutend \(-5\,\mathrm{m}\) nach vorne gehen. Anstatt \(-10\,\mathrm{m}\) (Meter) nach rechts abzumessen, kann man gleichbedeutend \(+10\,\mathrm{m}\) nach links abmessen. Anstatt \(-170^\circ\) entgegen dem Uhrzeigersinn abzumessen, kann man gleichbedeutend \(+ 170^\circ\) im Uhrzeigersinn abmessen.Negative Winkel
h) Quiz
Programm
Nachfolgend ein Programm, dass Sie ausführen können: Auf dem PC z.B. mit Anaconda. Im Browser (online) in drei Schritten: Copy: Source Code in die Zwischenablage kopieren. Paste: Source Code als Python-Notebook einfügen z.B. auf: JupyterLab oder Play: Ausführen. Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.SymPy
# -*- coding: utf-8 -*-
from sympy.physics.units import *
from sympy import *
# Units:
(mm, cm) = ( m/1000, m/100 )
Newton = kg*m/s**2
kN = 10**3*Newton
Pa = Newton/m**2
MPa = 10**6*Pa
GPa = 10**9*Pa
deg = pi/180
half = S(1)/2
# Rounding:
import decimal
from decimal import Decimal as DX
from copy import deepcopy
def iso_round(obj, pv,
rounding=decimal.ROUND_HALF_EVEN):
import sympy
"""
Rounding acc. to DIN EN ISO 80000-1:2013-08
place value = Rundestellenwert
"""
assert pv in set([
# place value # round to:
"1", # round to integer
"0.1", # 1st digit after decimal
"0.01", # 2nd
"0.001", # 3rd
"0.0001", # 4th
"0.00001", # 5th
"0.000001", # 6th
"0.0000001", # 7th
"0.00000001", # 8th
"0.000000001", # 9th
"0.0000000001", # 10th
])
objc = deepcopy(obj)
try:
tmp = DX(str(float(objc)))
objc = tmp.quantize(DX(pv), rounding=rounding)
except:
for i in range(len(objc)):
tmp = DX(str(float(objc[i])))
objc[i] = tmp.quantize(DX(pv), rounding=rounding)
return objc
prec = "0.01"
v = Matrix([3, 4])
p = -4 *deg
lin = True
# lin = False
pprint("\nv:")
tmp = v
pprint(v)
pprint("\nφ / deg:")
tmp = p / deg
pprint(tmp)
if lin:
pprint("\nInfinitesimal Rotation.")
R = Matrix([[1, p],[-p, 1]])
else:
pprint("\nFinite Rotation.")
c, s = cos(p), sin(p)
R = Matrix([[c, s],[-s, c]])
# pprint("\nR:")
# tmp = R
# tmp = iso_round(tmp,prec)
# pprint(tmp)
pprint("\n(vx\u0304, vy\u0304):")
vb = R*v
tmp = vb
tmp = iso_round(tmp,prec)
pprint(tmp)
v:
⎡3⎤
⎢ ⎥
⎣4⎦
φ / deg:
10
Infinitesimal Rotation.
(vx̄, vȳ):
⎡3.7 ⎤
⎢ ⎥
⎣3.48⎦