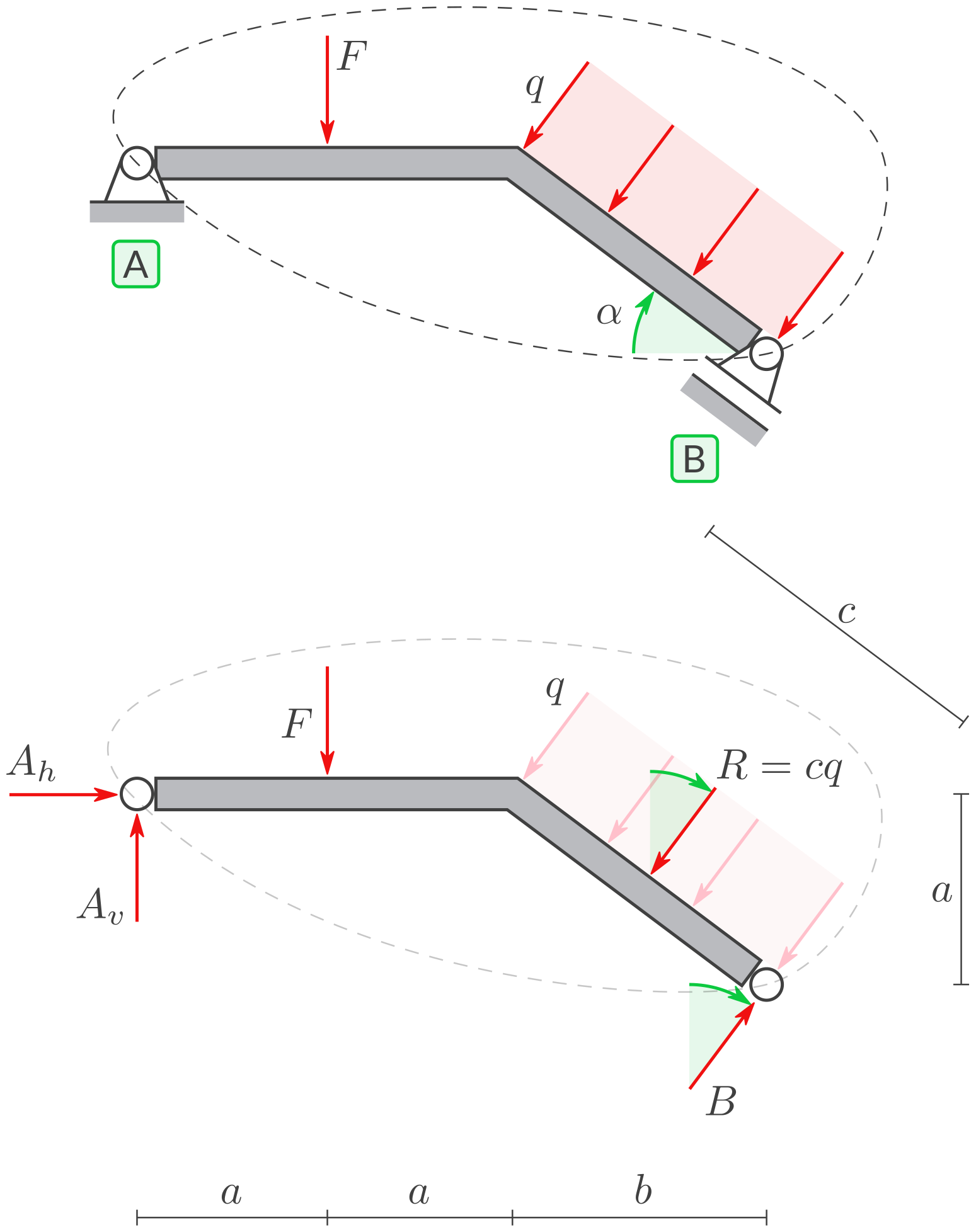
1.5.A

../../../_images/1.5.A.png

Gegebene Symbole: \(F, q, a.\) Und davon abhängig \(b=\tfrac 4 3 a.\)

Gegebene Größen:

\[\begin{split}F &= 100 \,\mathrm{N} \\ q &= 24 \, \tfrac{\mathrm{N}}{\mathrm{m}} \\ a &= 3 \,\mathrm{m}\end{split}\]

Und davon abhängig:

\[\begin{split}b &=\tfrac 4 3 a\\ &= 4 \,\mathrm{m}\end{split}\]

Berechnen Sie die Lagerreaktionen. Gehen Sie wie folgt vor.

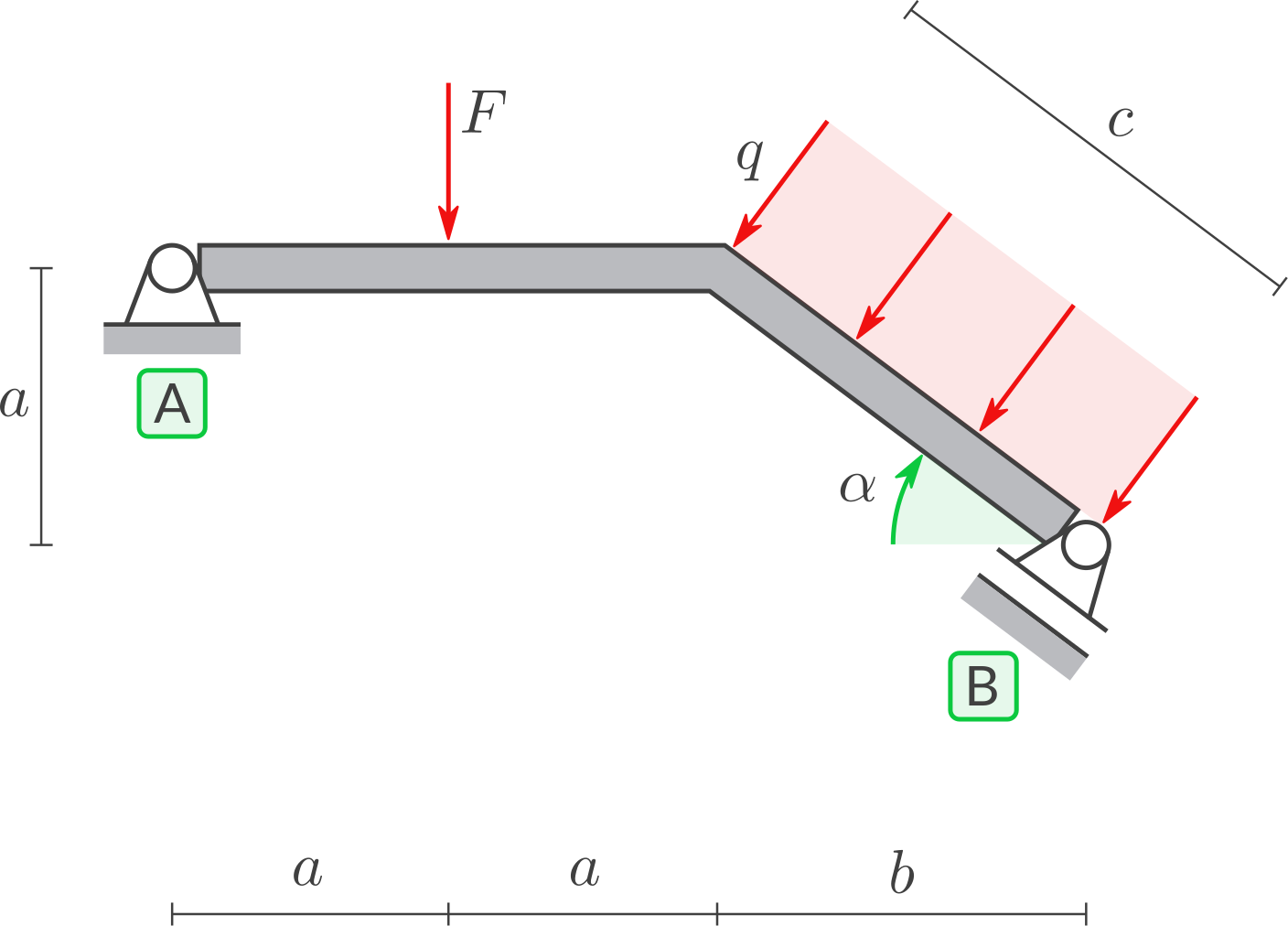
a) Geometrie

Für die gegebenen Symbole: Berechnen Sie:

\[\begin{split}c &= \ldots \\ \cos\alpha &= \ldots \\ \sin\alpha &= \ldots\end{split}\]

Lösung

\[c = \sqrt{a^2 + b^2}\]

Und mit diesem \(c\):

\[\begin{split}\cos\alpha &= \tfrac b c \\ \sin\alpha &= \tfrac a c\end{split}\]

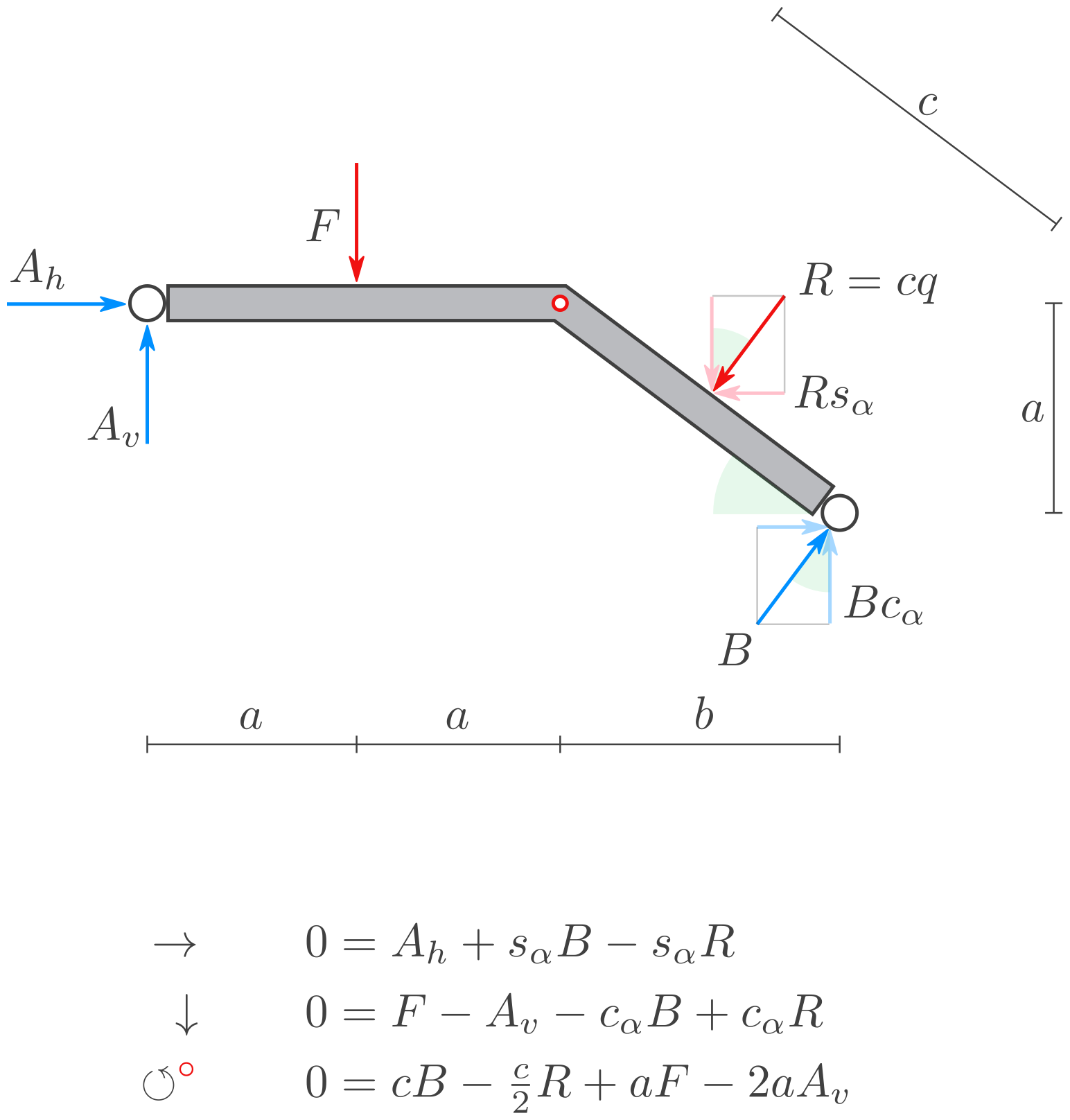
b) Freikörperbild

  • Berechnen Sie die Resultierende der verteilten Kraft.

  • Schneiden Sie an den Lagern frei, so dass die Auflagerkräfte sichtbar werden.

  • Zeichnen Sie den Balken in einem Freikörperbild.

Lösung

../../../_images/1.5.A_1.png

c) Lagerreaktionen

Für die gegebenen Größen: Berechnen Sie alle Lagerreaktionen.

Lösung

../../../_images/1.5.A_3.png

Lösung:

\[\begin{split}A_h &= 0 \,\mathrm{N} \\ A_v &= 100 \,\mathrm{N} \\ B &= 120 \,\mathrm{N}\end{split}\]

SymPy

Nachfolgend ein Programm, dass Sie ausführen können:

  • Auf dem PC z.B. mit Anaconda.

  • Im Browser (online) in drei Schritten:

    1. Copy: Source Code in die Zwischenablage kopieren.

    2. Paste: Source Code als Python-Notebook einfügen z.B. auf:

    3. Play: Ausführen.

from sympy.physics.units import *
from sympy import *

# Units:
(k, M, G ) = ( 10**3, 10**6, 10**9 )
(mm, cm) = ( m/1000, m/100 )
Pa     = newton/m**2
MPa    = M*Pa
GPa    = G*Pa
kN     = k*newton
deg    = pi/180
half = S(1)/2

# ---

a, b = var("a, b", positive=True)
F, q = var("F, q", real = True)

sub_list=[
    (F, 100*newton),
    (q, 24*newton/m),
    (a, 3*m),
    ]

b = 4*a/3
c = sqrt(a**2 + b**2)

pprint("R:")
R = c*q
tmp = R
pprint(tmp)
pprint("R / N:")
tmp = tmp.subs(sub_list)
tmp /= newton
pprint(tmp)

# Unknowns:
Ah, Av, B = var("A_h A_v B")

pprint("\nca, sa:")
ca, sa = b/c, a/c
pprint(ca)
pprint(sa)

eq1 = Eq(0, Ah + B*sa - R*sa)
eq2 = Eq(0, F - Av - B*ca + R*ca)
eq3 = Eq(0, c*B - c/2*R + a*F - 2*a*Av)

# Solve for unknowns:
eqs = [eq1, eq2, eq3]
sol = solve(eqs, [Ah, Av, B])

pprint("\nAh:")
tmp = sol[Ah]
pprint(tmp)
pprint("\nAh / N:")
tmp = tmp.subs(sub_list)
tmp /= newton
pprint(tmp)

pprint("\nAv:")
tmp = sol[Av]
pprint(tmp)
pprint("\nAv / N:")
tmp = tmp.subs(sub_list)
tmp /= newton
pprint(tmp)

pprint("\nB:")
tmp = sol[B]
pprint(tmp)
pprint("\nB / N:")
tmp = tmp.subs(sub_list)
tmp /= newton
pprint(tmp)

R:
5⋅a⋅q
─────
  3  
R / N:
120
       
ca, sa:
4/5
3/5
   
Ah:
  9⋅F   25⋅a⋅q
- ─── + ──────
   49     98  
       
Ah / N:
0
   
Av:
37⋅F   50⋅a⋅q
──── + ──────
 49     147  
       
Av / N:
100
  
B:
15⋅F   365⋅a⋅q
──── + ───────
 49      294  
      
B / N:
120

Statt SymPy lieber anderes CAS (Computeralgebrasystem) verwenden? Eine Auswahl verschiedener CAS gibt es hier.