B2.A

Video

Klassische Lösung

siehe 2.4.2.J

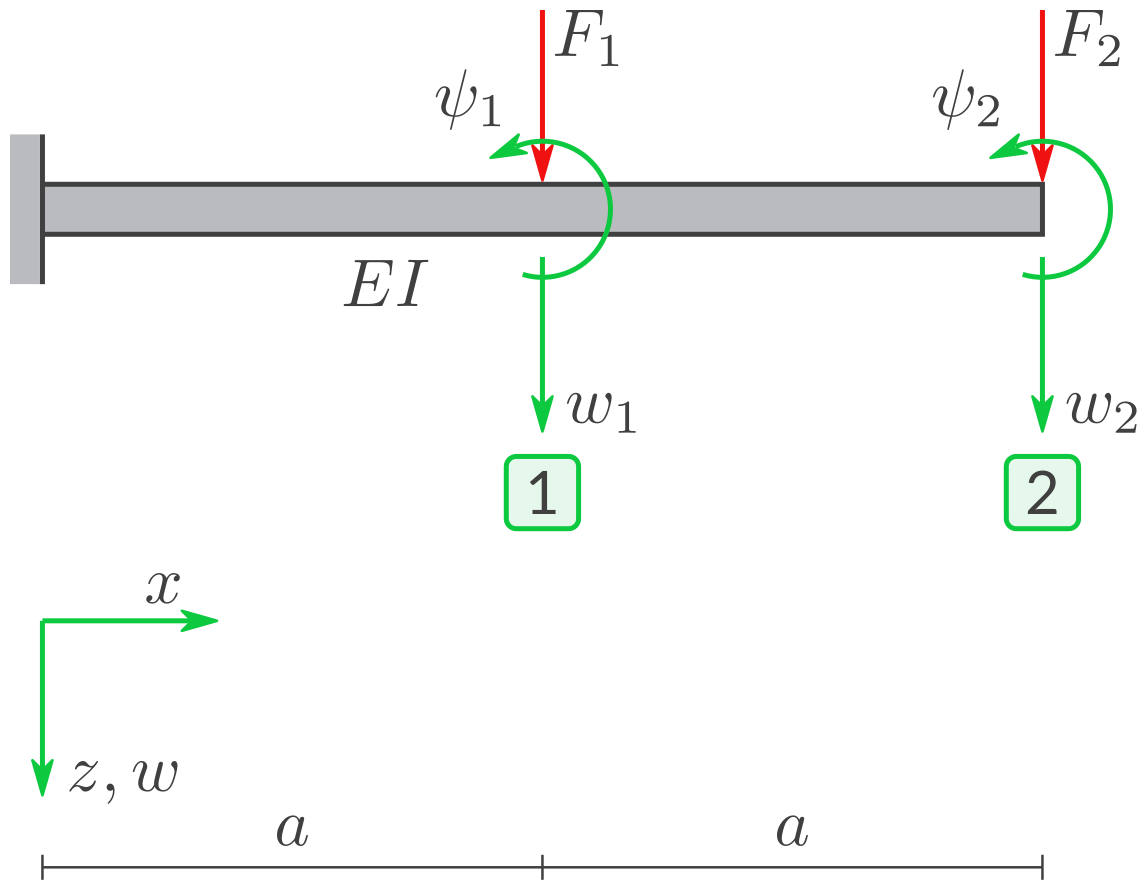
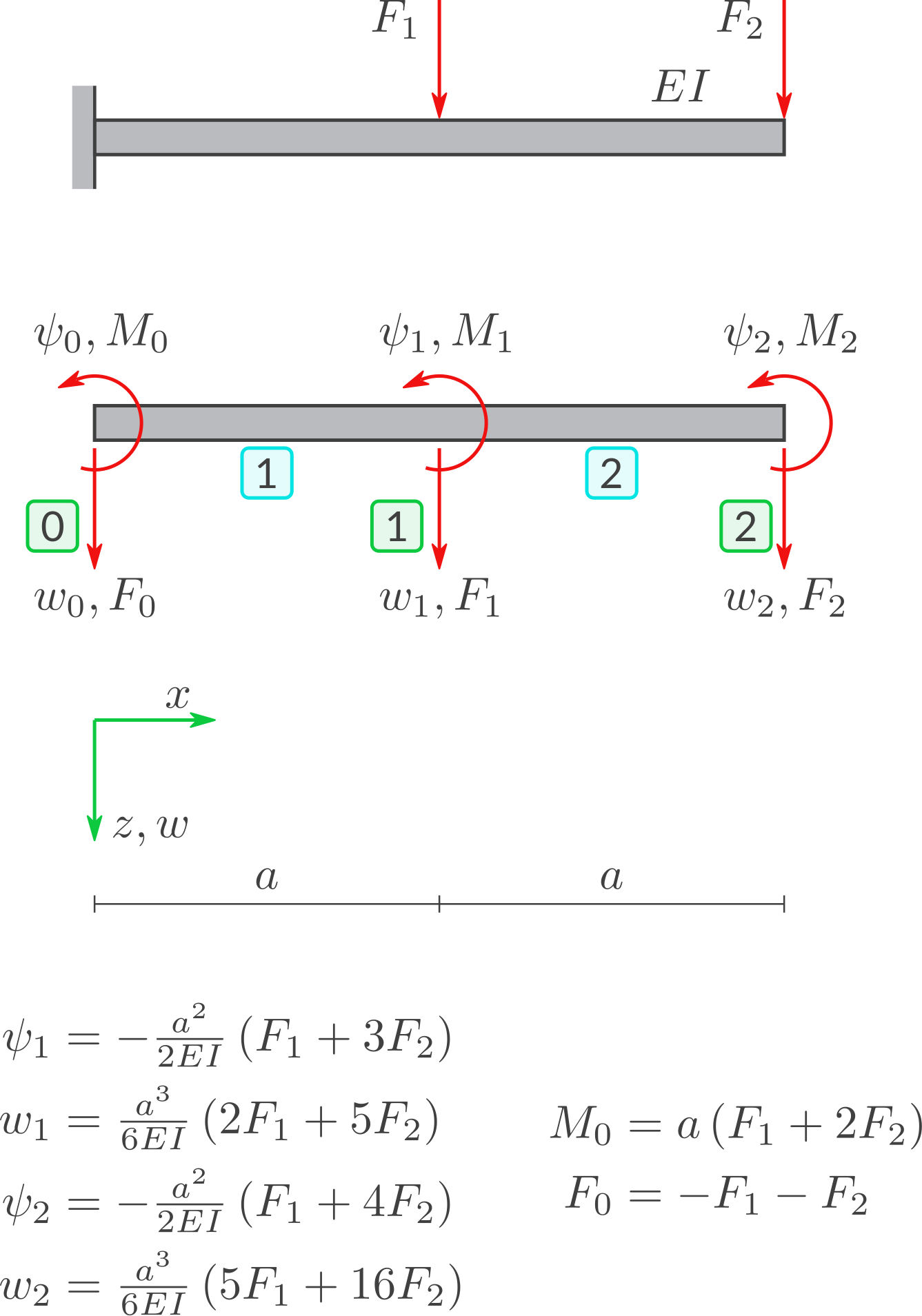
Gegebene Symbole: \(a, EI, F_1, F_2.\)

Ein Kragbalken ist belastet durch zwei Kräfte \(F_1\) und \(F_2\) und erleidet Verformungen \(w_1, \psi_1, w_2, \psi_2.\) Untersuchen Sie die Struktur. Gehen Sie wie folgt vor.

Lösung vorab

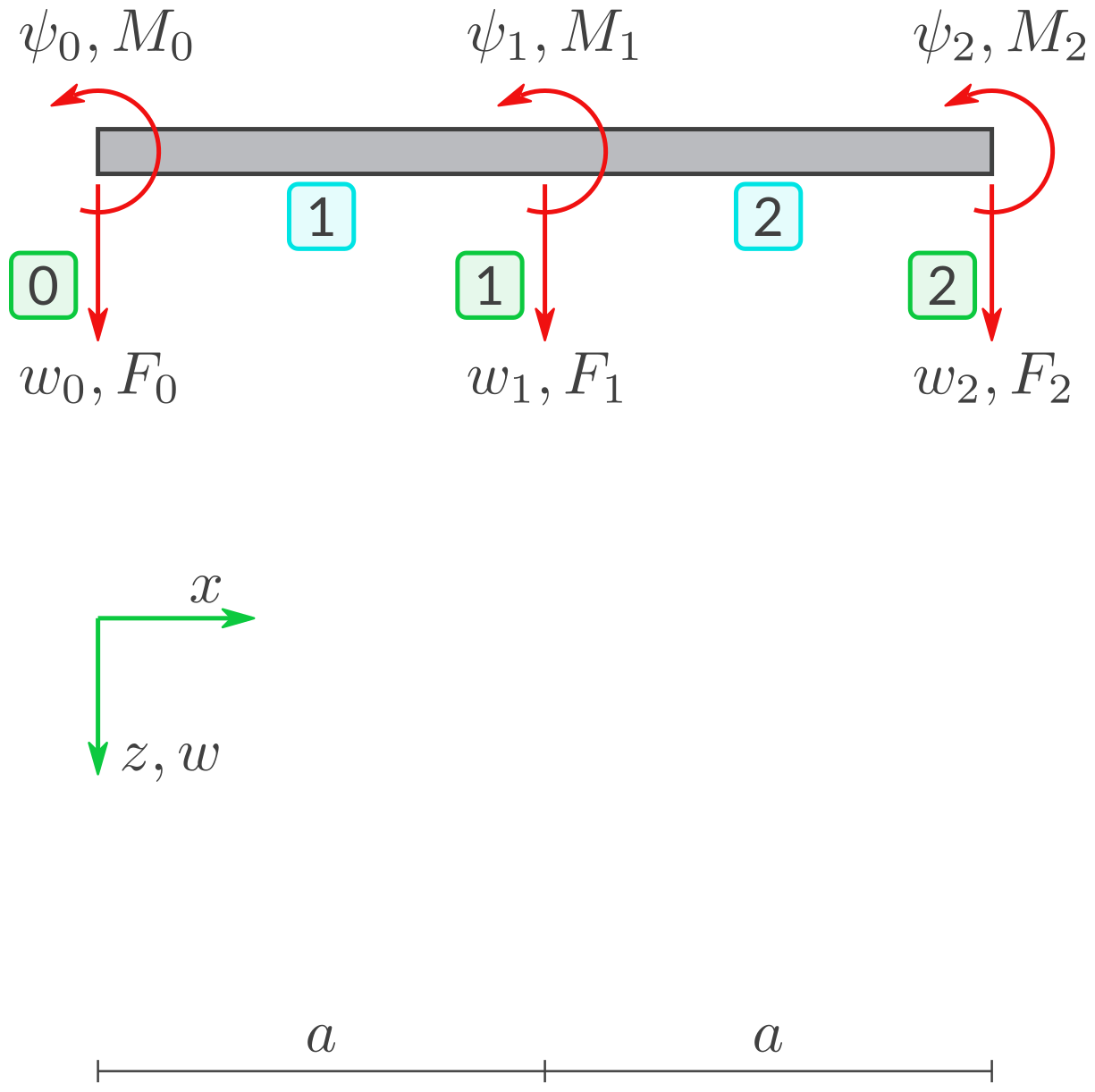
a) Elemente und Knoten

Definieren Sie zwei Finite Balken-Elemente wie in Balken-Element B2.

Lösung

b) Erweiterte Element-Steifigkeitsmatrizen

Berechnen Sie:

• \(k_1^|\): Die erweiterte Element-Steifigkeitsmatrix von Element 1, und zwar im „Element-Format“:

• \(k_2^|\): Die erweiterte Element-Steifigkeitsmatrix von Element 2 im „Element-Format“.

• \(K_1^|\): Die erweiterte Element-Steifigkeitsmatrix von Element 1 im „System-Format“.

• \(K_2^|\): Die erweiterte Element-Steifigkeitsmatrix von Element 2 im „System-Format“.

Lösung

\begin{align*} k_1^| \!&=\! \tfrac{EI}{a^3} \! \left[ \begin{array}{cccc|c} 4 a^2 & -6 a & 2 a^2 & 6 a & \psi_0 \\ & 12 & -6 a & -12 & w_0 \\ & & 4 a^2 & 6 a & \psi_1 \\ \mathsf{sym} & & & 12 & w_1 \end{array} \right] \\ k_2^| \!&=\! \tfrac{EI}{a^3} \! \left[ \begin{array}{cccc|c} 4 a^2 & -6 a & 2 a^2 & 6 a & \psi_1 \\ & 12 & -6 a & -12 & w_1 \\ & & 4 a^2 & 6 a & \psi_2 \\ \mathsf{sym} & & & 12 & w_2 \end{array} \right] \\ K_1^| \!&=\! \tfrac{EI}{a^3} \! \left[ \begin{array}{cccccc|c} 4 a^2 & -6 a & 2 a^2 & 6 a & 0 & 0 & \psi_0 \\ -6 a & 12 & -6 a & -12 & 0 & 0 & w_0 \\ 2 a^2 & -6 a & 4 a^2 & 6 a & 0 & 0 & \psi_1 \\ 6 a & -12 & 6 a & 12 & 0 & 0 & w_1 \\ 0 & 0 & 0 & 0 & 0 & 0 & \psi_2 \\ 0 & 0 & 0 & 0 & 0 & 0 & w_2 \end{array} \right] \\ K_2^| \!&=\! \tfrac{EI}{a^3} \! \left[ \begin{array}{cccccc|c} 0 & 0 & 0 & 0 & 0 & 0 & \psi_0 \\ 0 & 0 & 0 & 0 & 0 & 0 & w_0 \\ 0 & 0 & 4 a^2 & -6 a & 2 a^2 & 6 a & \psi_1 \\ 0 & 0 & -6 a & 12 & -6 a & -12 & w_1 \\ 0 & 0 & 2 a^2 & -6 a & 4 a^2 & 6 a & \psi_2 \\ 0 & 0 & 6 a & -12 & 6 a & 12 & w_2 \end{array} \right] \end{align*}

c) System-Steifigkeitsmatrix

Verwenden Sie:

• \(K\): Die System-Steifigkeitsmatrix.

• \(u\): Die Deformationen.

• \(f\): Die äußeren Knotenlasten.

\[\begin{split}u = \begin{bmatrix} \psi_0 \\ w_0 \\ \psi_1 \\ w_1 \\ \psi_2 \\ w_2 \end{bmatrix} \qquad f = \begin{bmatrix} M_0 \\ F_0 \\ M_1 \\ F_1 \\ M_2 \\ F_2 \end{bmatrix}\end{split}\]

Berechnen Sie die System-Steifigkeitsmatrix \(K\). Und notieren Sie in Matrix-Notation:

\[K u = f\]

Lösung

Die System-Steifigkeitsmatrix ist die „Summe“ der Element-Steifigkeitsmatrizen im „System-Format“, so dass:

\begin{align*} \underbrace{ \tfrac{EI}{a^3} \! \left[ \begin{array}{cccccc} 4 a^2 & -6 a & 2 a^2 & 6 a & 0 & 0 \\ -6 a & 12 & -6 a & -12 & 0 & 0 \\ 2 a^2 & -6 a & 8 a^2 & 0 & 2 a^2 & 6 a \\ 6 a & -12 & 0 & 24 & -6 a & -12 \\ 0 & 0 & 2 a^2 & -6 a & 4 a^2 & 6 a \\ 0 & 0 & 6 a & -12 & 6 a & 12 \end{array} \right] }_K \! \underbrace{ \left[ \begin{array}{c} \psi_0 \\ w_0 \\ \psi_1 \\ w_1 \\ \psi_2 \\ w_2 \end{array} \right] }_u \!&=\! \underbrace{ \left[ \begin{array}{c} M_0 \\ F_0 \\ M_1 \\ F_1 \\ M_2 \\ F_2 \end{array} \right] }_f \tag{1} \end{align*}

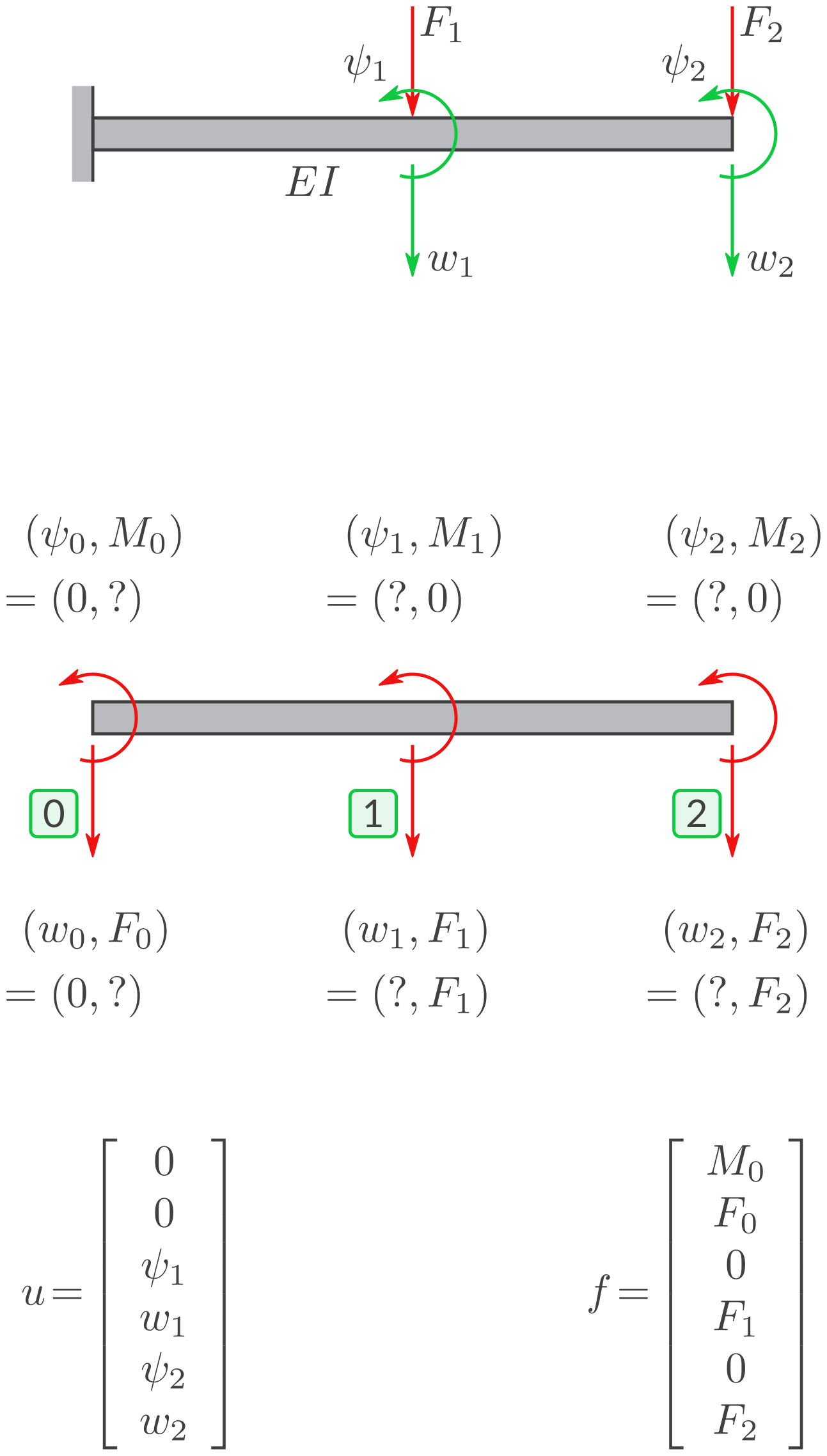
d) Randbedingungen

Passen Sie \(u\) und \(f\) an die Randbedingungen an.

\[\begin{split}u = \begin{bmatrix} \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \end{bmatrix} \qquad f = \begin{bmatrix} \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \\ \ldots \end{bmatrix}\end{split}\]

Lösung

e) Verformungen

Berechnen Sie \(\psi_1, w_1, \psi_2, w_2\). Zeigen Sie, dass:

\begin{align*} \left[ \begin{array}{c} \psi_1 \\ w_1 \\ \psi_2 \\ w_2 \end{array} \right] \!&=\! \tfrac{a^2}{6 EI} \!\left[ \begin{array}{c} - 3 F_{1} -9 F_{2} \\ a( 2 F_{1} + 5 F_{2} ) \\ - 3 F_{1} -12 F_{2} \\ a ( 5 F_{1} + 16 F_{2} ) \end{array} \right] \end{align*}

Lösung

Folgende Gleichung beschreibt das System:

\[\begin{split}\tfrac{EI}{a^3} \begin{bmatrix} 4 a^2 & -6 a & 2 a^2 & 6 a & 0 & 0 \\ -6 a & 12 & -6 a & -12 & 0 & 0 \\ 2 a^2 & -6 a & 8 a^2 & 0 & 2 a^2 & 6 a \\ 6 a & -12 & 0 & 24 & -6 a & -12 \\ 0 & 0 & 2 a^2 & -6 a & 4 a^2 & 6 a \\ 0 & 0 & 6 a & -12 & 6 a & 12 \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ \psi_1 \\ w_1 \\ \psi_2 \\ w_2 \end{bmatrix} &= \begin{bmatrix} M_0 \\ F_0 \\ 0 \\ F_1 \\ 0 \\ F_2 \end{bmatrix}\end{split}\]

Dies sind sechs Gleichungen, aus denen die sechs Unbekannten \(\psi_1, w_1, \psi_2, w_2, M_0, F_0\) berechnet werden können. Die vier letzten Gleichungen sind vier Gleichungen, aus denen die vier Unbekannten \(\psi_1, w_1, \psi_2, w_2\) berechnet werden können. Die vier letzten Gleichungen sind:

\begin{align*} \tfrac{EI}{a^3} \left[ \begin{array}{cccc} 8 a^2 & 0 & 2 a^2 & 6 a \\ 0 & 24 & -6 a & -12 \\ 2 a^2 & -6 a & 4 a^2 & 6 a \\ 6 a & -12 & 6 a & 12 \end{array} \right] \left[ \begin{array}{c} \psi_1 \\ w_1 \\ \psi_2 \\ w_2 \end{array} \right] \!&=\! \left[ \begin{array}{c} 0 \\ F_1 \\ 0 \\ F_2 \end{array} \right] \end{align*}

Berechnung der vier Unbekannten \(\psi_1, w_1, \psi_2, w_2\) aus diesem linearen Gleichungssystems liefert wie behauptet:

\begin{align*} \left[ \begin{array}{c} \psi_1 \\ w_1 \\ \psi_2 \\ w_2 \end{array} \right] \!&=\! \tfrac{a^2}{6 EI} \!\left[ \begin{array}{c} - 3 F_{1} -9 F_{2} \\ a( 2 F_{1} + 5 F_{2} ) \\ - 3 F_{1} -12 F_{2} \\ a ( 5 F_{1} + 16 F_{2} ) \end{array} \right] \end{align*}

f) Kräfte

Berechnen Sie die Lagerreaktionen.

Lösung

Die Lagerreaktionen \(M_0\) und \(F_0\) lassen sich mit den jetzt bekannten \(\psi_1, w_1, \psi_2, w_2\) aus den ersten beiden Gleichungen des Systems berechnen. Die ersten beiden Gleichungen sind:

\begin{align*} \tfrac{EI}{a^3} \! \left[ \begin{array}{cccccc} 2 a^2 & 6 a \\ -6 a & -12 \\ \end{array} \right] \left[ \begin{array}{c} \psi_1 \\ w_1 \\ \end{array} \right] \!&=\! \left[ \begin{array}{c} M_0 \\ F_0 \\ \end{array} \right] \end{align*}

Einsetzen von den zuvor berechneten \(\psi_1, w_1, \psi_2, w_2\) liefert:

\begin{align*} \left[ \begin{array}{c} M_{0} \\ F_0 \\ \end{array} \right] \!=\! \left[ \begin{array}{c} a \left(F_{1} + 2 F_{2}\right)\\ - F_{1} - F_{2}\\ \end{array} \right] \end{align*}

g) Ergebnis für gegebene Größen

Berechnen Sie \(w_2\) in \(\mathrm{mm}\) (Millimeter) für die folgenden Größen:

\[\begin{split}F_1 &= 10 \,\mathrm{kN} \\ F_2 &= 10 \,\mathrm{kN} \\ a &= 1 \,\mathrm{m} \\ E &= 210 \,\mathrm{GPa} \\ I &= 318 \,\mathrm{cm}^4\end{split}\]

Runden Sie auf Rundestellenwert \(0{,}01\). Zeigen Sie, dass:

\[w_2 \stackrel{\small{0{,}01}}{\approx} 52{,}41 \,\mathrm{mm}\]

Lösung

Einsetzen der gegebenen Größen liefert:

\[w_2 \stackrel{\small{0{,}01}}{\approx} 52{,}41 \,\mathrm{mm}\]

Zur Veranschaulichung

• \(E= 210 \,\mathrm{GPa}\) entspricht dem E-Modul von Stahl.

• \(I = 318 \,\mathrm{cm}^4\) entspricht dem \(I_{yy}\) eines IPE 120.

  

  DIN 1025-5: IPE 120: \(I_{yy}\stackrel{1.0}{\approx} 318 \,\mathrm{cm}^4\)

• \(F_1 = F_2 = 10 \,\mathrm{kN}\) entspricht ca. der Gewichtskraft eines VW Polo.

  

  VW Polo: Masse ca. \(1000\,\mathrm{kg}\), Gewichtskraft ca. \(1000\,\mathrm{kg} \cdot 10\,\tfrac{\mathrm{m}}{\mathrm{s}^2} = 10 \,\mathrm{kN}\)

Balken-Aufgaben in SymPy gelöst

Lösung einiger Balken-Aufgaben in einem Programm hier.