Tags: Video

R2.A

Video

Gegeben

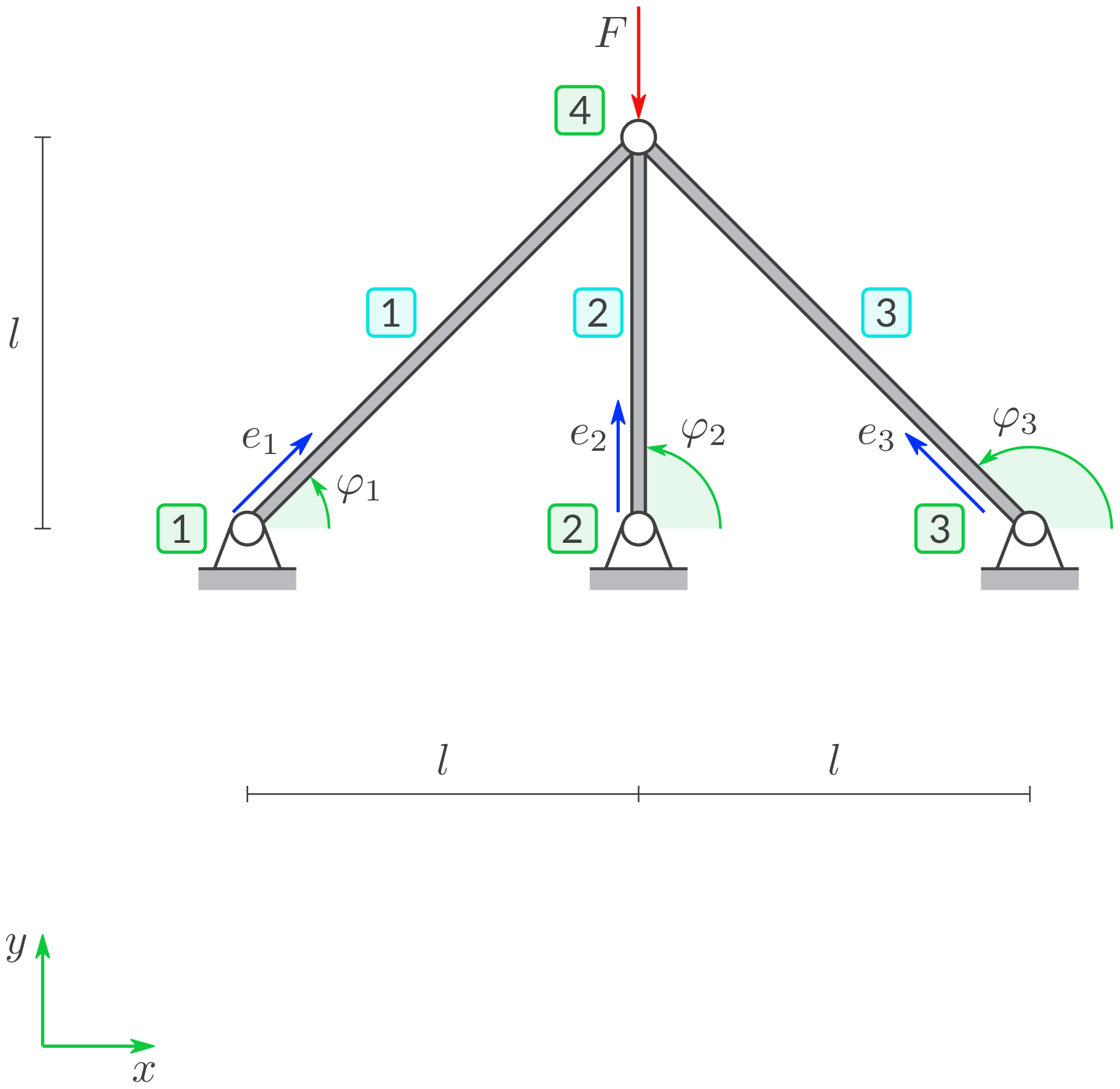
../../../../_images/R2.A.png

Symbole:

\[F, l, E, A\]

E-Modul \(E\) und Querschnittsfläche \(A\) für alle Stäbe gleich.

Klassische Lösung

siehe 2.1.Q

a) Elemente und Knoten

Das System besteht aus den drei Stab-Elementen 1, 2 und 3 mit Einheitsvektoren \(\boldsymbol e_1, \boldsymbol e_2, \boldsymbol e_3.\) Füllen Sie folgende Tabelle aus:

Element

Länge

Knoten

Winkelposition

1

2

3

Lösung

../../../../_images/R2.A.png

Element

Länge

Knoten

Winkelposition

1

\(\sqrt 2 l\)

1-4

\(\varphi_1 = 45 ^\circ\)

2

\(l\)

2-4

\(\varphi_2 = 90 ^\circ\)

3

\(\sqrt 2 l\)

3-4

\(\varphi_3 = 135 ^\circ\)

b) Erweiterte Matrizen

Berechnen Sie:

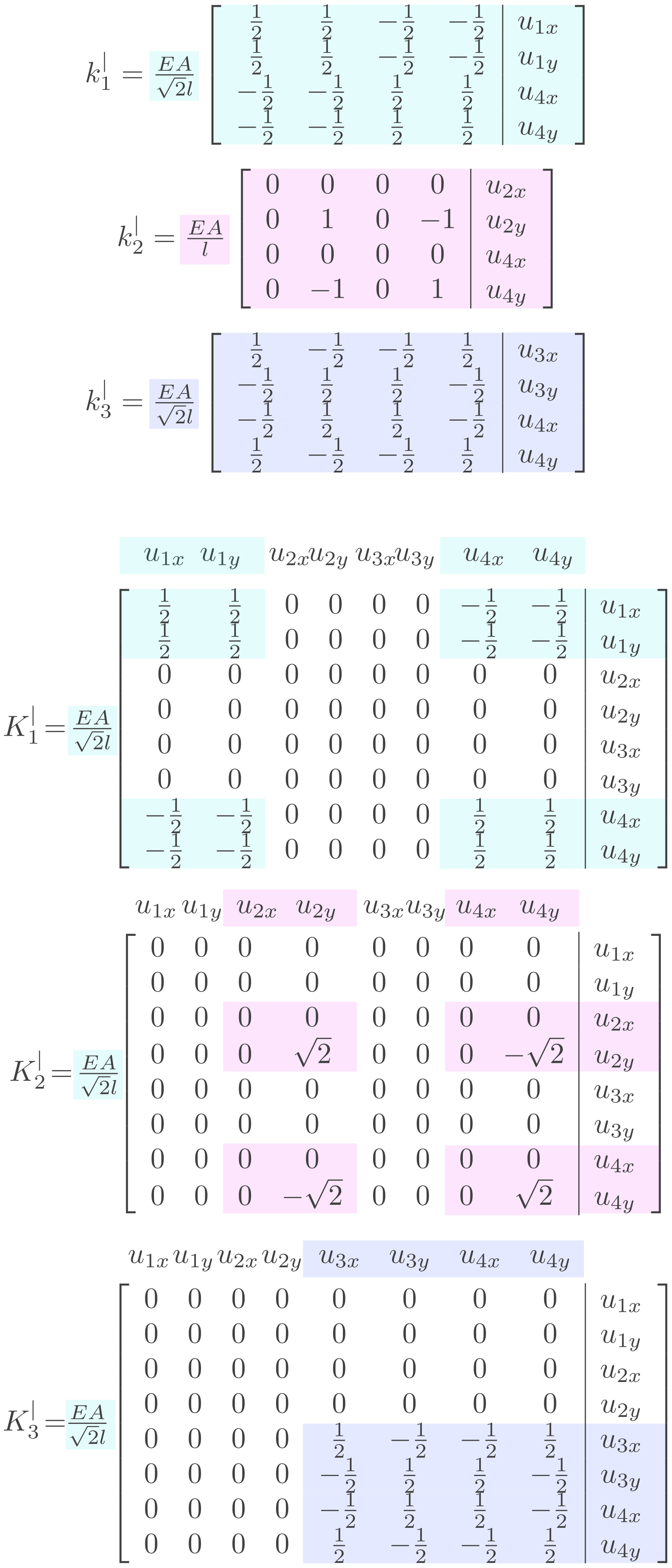
  • die erweiterten Element-Steifigkeitsmatrizen im „Element-Format“ \(k_1^|, k_2^|, k_3^|\).

  • die erweiterten Element-Steifigkeitsmatrizen im „System-Format“ \(K^|_1, K^|_2, K^|_3\) mit dem Faktor \(\tfrac{EA}{\sqrt 2 l}\) vor jeder der drei Matrizen.

Lösung

../../../../_images/R2.A_sort.png

c) Erweiterte System-Steifigkeitsmatrix

Berechnen Sie die erweiterte System-Steifigkeitsmatrix \(K^|\).

Lösung

\begin{align*} K^| &= K_1^| + K_3^| + K_3^| \\ &= \tfrac{EA}{\sqrt 2 l} \left[ \begin{array}{cccccccc|c} \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} & u_{1x} \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} & u_{1y} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & u_{2x} \\ 0 & 0 & 0 & \sqrt{2} & 0 & 0 & 0 & - \sqrt{2} & u_{2y} \\ 0 & 0 & 0 & 0 & \frac{1}{2} & - \frac{1}{2} & - \frac{1}{2} & \frac{1}{2} & u_{3x} \\ 0 & 0 & 0 & 0 & - \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & - \frac{1}{2} & u_{3y} \\ - \frac{1}{2} & - \frac{1}{2} & 0 & 0 & - \frac{1}{2} & \frac{1}{2} & 1 & 0 & u_{4x} \\ - \frac{1}{2} & - \frac{1}{2} & 0 & - \sqrt{2} & \frac{1}{2} & - \frac{1}{2} & 0 & 1 + \sqrt{2} & u_{4y} \end{array} \right] \end{align*}

d) Randbedingungen und Lineares System

Seien die Knoten-Verschiebungen und die Knoten-Kräfte in den folgenden Spaltenmatrizen \(u\) und \(f\) zusammengefasst:

\begin{align*} u = \begin{bmatrix} u_{1x} \\ u_{1y} \\ u_{2x} \\ u_{2y} \\ u_{3x} \\ u_{3y} \\ u_{4x} \\ u_{4y} \\ \end{bmatrix} \quad,\quad f = \begin{bmatrix} F_{1x} \\ F_{1y} \\ F_{2x} \\ F_{2y} \\ F_{3x} \\ F_{3y} \\ F_{4x} \\ F_{4y} \\ \end{bmatrix} \end{align*}

Passen Sie die Spaltenmatrizen \(u\) und \(f\) an die geometrischen und physikalischen Randbedingungen an. Und notieren Sie die folgende Gleichung mit den angepassten Spaltenmatrizen.

\begin{align*} K u = f \end{align*}

Lösung

\begin{align*} u = \begin{bmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ u_{4x}\\ u_{4y}\\ \end{bmatrix} \quad,\quad f = \begin{bmatrix} F_{1x}\\ F_{1y}\\ F_{2x}\\ F_{2y}\\ F_{3x}\\ F_{3y}\\ 0 \\ -F \\ \end{bmatrix} \end{align*}
\begin{align*} \tfrac{EA}{\sqrt 2 l} \! \! \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \sqrt{2} & 0 & 0 & 0 & - \sqrt{2} \\ 0 & 0 & 0 & 0 & \frac{1}{2} & - \frac{1}{2} & - \frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 0 & 0 & - \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & - \frac{1}{2} \\ - \frac{1}{2} & - \frac{1}{2} & 0 & 0 & - \frac{1}{2} & \frac{1}{2} & 1 & 0 \\ - \frac{1}{2} & - \frac{1}{2} & 0 & - \sqrt{2} & \frac{1}{2} & - \frac{1}{2} & 0 & 1 + \sqrt{2} \end{bmatrix} \!\! \begin{bmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ u_{4x}\\ u_{4y}\\ \end{bmatrix} \! \! = \! \! \begin{bmatrix} F_{1x}\\ F_{1y}\\ F_{2x}\\ F_{2y}\\ F_{3x}\\ F_{3y}\\ 0 \\ -F \\ \end{bmatrix} \end{align*}

e) Verschiebungen

Berechnen Sie:

\begin{align*} \begin{bmatrix} u_{4x} \\ u_{4y} \\ \end{bmatrix} = \begin{bmatrix} \ldots \\ \ldots \\ \end{bmatrix} \tfrac{Fl}{EA} \end{align*}

Für folgende Größen:

\begin{align*} F &= 5\,\mathrm{kN} \\ E &= 200\,\mathrm{GPa} \\ A &= 25\,\mathrm{mm}^2 \\ l &= 1707\,\mathrm{mm} \end{align*}

Berechnen Sie außerdem \(u_{4y}\) in \(\mathrm{mm}\) (Millimeter) und gerundet auf Rundestellenwert \(0{,}0001\):

\begin{align*} u_{4y} \stackrel{\scriptscriptstyle{0{,}0001}}{\approx} \ldots \, \mathrm{mm} \end{align*}

Lösung

Die 7. und 8. Gleichung des Gleichungssystems liefern:

\begin{align*} \begin{bmatrix} u_{4x} \\ u_{4y} \\ \end{bmatrix} &= \begin{bmatrix} 0 \\ -2 + \sqrt 2 \\ \end{bmatrix} \tfrac{Fl}{EA} \\ \\ u_{4y} &\stackrel{\scriptscriptstyle{0{,}0001}}{\approx}-0{,}9999\,\mathrm{mm} \end{align*}

f) Lagerreaktionen

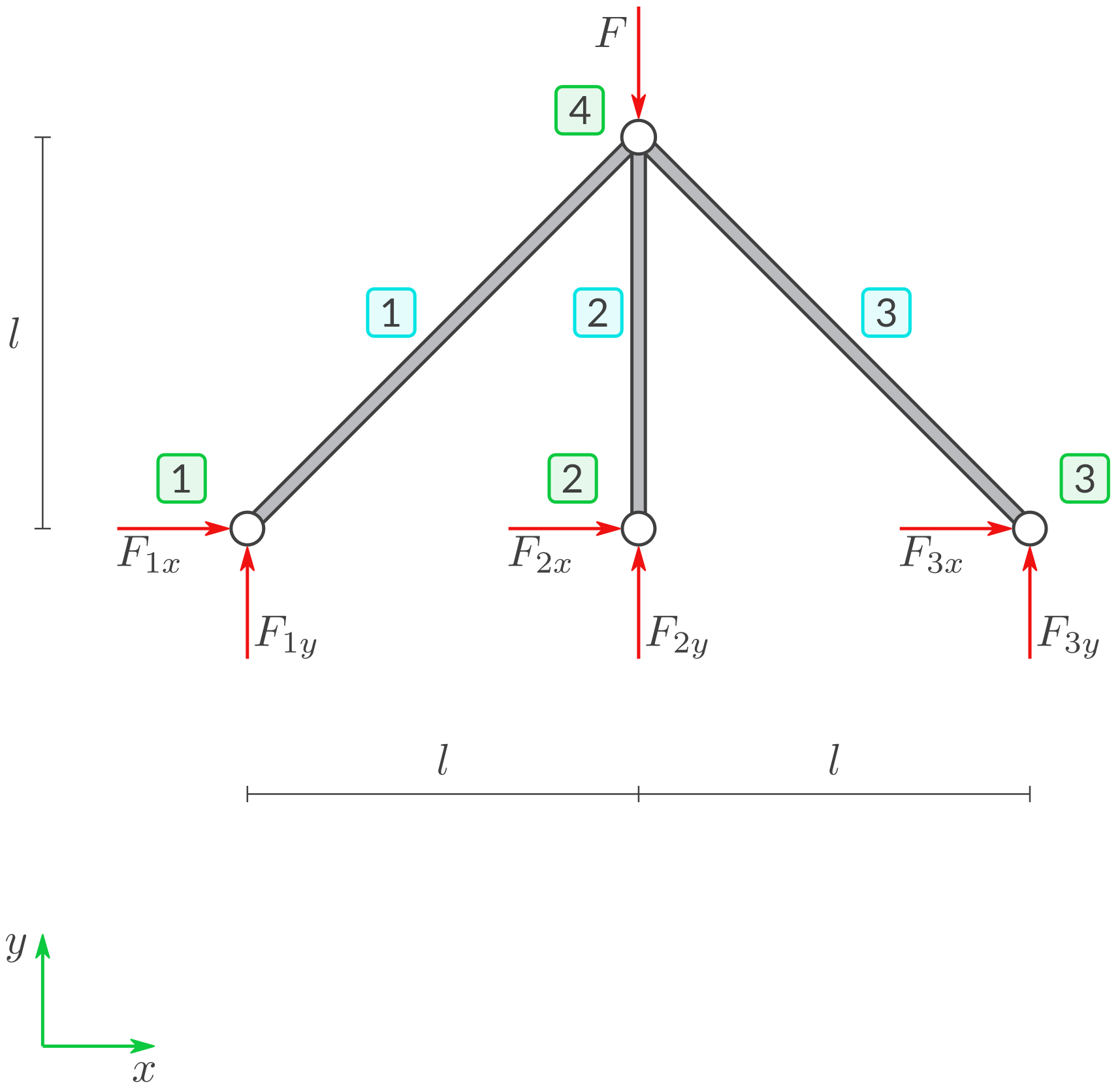
../../../../_images/R2.A_2.png

Berechnen Sie für dieselben Größen die \((x,y)\)-Komponenten der Lagerreaktionen. Und zwar in \(\mathrm{N}\) (Newton) und gerundet auf Rundestellenwert \(0{,}1\):

\begin{align*} \begin{bmatrix} F_{1x} \\ F_{1y} \\ \end{bmatrix} \stackrel{\scriptscriptstyle{0{,}1}}{\approx} \begin{bmatrix} \ldots \\ \ldots \\ \end{bmatrix} \mathrm{N} \\ \begin{bmatrix} F_{2x} \\ F_{2y} \\ \end{bmatrix} \stackrel{\scriptscriptstyle{0{,}1}}{\approx} \begin{bmatrix} \ldots \\ \ldots \\ \end{bmatrix} \mathrm{N} \\ \begin{bmatrix} F_{3x} \\ F_{3y} \\ \end{bmatrix} \stackrel{\scriptscriptstyle{0{,}1}}{\approx} \begin{bmatrix} \ldots \\ \ldots \\ \end{bmatrix} \mathrm{N} \end{align*}

Lösung

Einsetzen der berechneten Verschiebungen in das Gleichungssystem liefert:

\begin{align*} \begin{bmatrix} F_{1x} \\ F_{1y} \\ \end{bmatrix} &= \begin{bmatrix} - \frac{1}{2} + \frac{\sqrt{2}}{2}\\- \frac{1}{2} + \frac{\sqrt{2}}{2} \end{bmatrix} F \\ \begin{bmatrix} F_{2x} \\ F_{2y} \\ \end{bmatrix} &= \begin{bmatrix} 0\\- \sqrt{2} + 2 \end{bmatrix} F \\ \begin{bmatrix} F_{3x} \\ F_{3y} \\ \end{bmatrix} &= \begin{bmatrix} - \frac{\sqrt{2}}{2} + \frac{1}{2}\\- \frac{1}{2} + \frac{\sqrt{2}}{2} \end{bmatrix} F \end{align*}

Details

Details zur Berechnung der Lagerreaktionen an Knoten 1:

Die ersten beiden Gleichungen des Gleichungssystems lauten:

\begin{align*} \tfrac{EA}{\sqrt 2 l} \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} \\ \end{bmatrix} \begin{bmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ u_{4x}\\ u_{4y}\\ \end{bmatrix} = \begin{bmatrix} F_{1x}\\ F_{1y}\\ \end{bmatrix} \end{align*}

Dies ist äquivalent zu den folgenden beiden Gleichungen:

\begin{align*} \tfrac{EA}{\sqrt 2 l} \begin{bmatrix} - \frac{1}{2} & - \frac{1}{2} \\ - \frac{1}{2} & - \frac{1}{2} \\ \end{bmatrix} \!\! \begin{bmatrix} u_{4x}\\ u_{4y}\\ \end{bmatrix} = \begin{bmatrix} F_{1x}\\ F_{1y}\\ \end{bmatrix} \end{align*}

Einsetzen der zuvor berechneten Verschiebungen liefert:

\begin{align*} \tfrac{Fl}{EA} \tfrac{EA}{\sqrt 2 l} \begin{bmatrix} - \frac{1}{2} & - \frac{1}{2} \\ - \frac{1}{2} & - \frac{1}{2} \\ \end{bmatrix} \begin{bmatrix} 0 \\ -2 + \sqrt 2 \\ \end{bmatrix} = \begin{bmatrix} F_{1x}\\ F_{1y}\\ \end{bmatrix} \end{align*}

Dasselbe neu aufgeschrieben ist:

\begin{align*} \tfrac{F}{\sqrt 2} \begin{bmatrix} - \frac{1}{2}(-2 + \sqrt 2) \\ - \frac{1}{2}(-2 + \sqrt 2) \\ \end{bmatrix} = \begin{bmatrix} F_{1x}\\ F_{1y}\\ \end{bmatrix} \end{align*}

Vertauschen der Seiten und Umformen liefert:

\begin{align*} \begin{bmatrix} F_{1x}\\ F_{1y}\\ \end{bmatrix} &= \begin{bmatrix} - \frac{1}{2\sqrt 2}(-2 + \sqrt 2) \\ - \frac{1}{2\sqrt 2}(-2 + \sqrt 2) \\ \end{bmatrix} F \\ &= \begin{bmatrix} - \frac{1}{2} + \frac{\sqrt{2}}{2}\\- \frac{1}{2} + \frac{\sqrt{2}}{2} \end{bmatrix} F \end{align*}

  • Die Einheit der Lagerreaktionen ist korrekt. Denn die Lagerreaktionen sind Kräfte.

  • Die x-Komponenten ist genauso groß ist wie die y-Komponente. Und das erwartet man auch. Denn die Resultierende muss genau in Richtung des Stabs 1 zeigen.

  • Das Vorzeichen der Komponenten ist plausibel. Denn man erwartet, dass das Lager für positives \(F\) eine Kraft wirkt die „nach rechts oben“ wirkt.

  • Die Lagerreaktionen an den Knoten 2 und 3 werden ganz ähnlich berechnet.

Einsetzen der gegebenen Größen liefert:

\begin{align*} \begin{bmatrix} F_{1x} \\ F_{1y} \\ \end{bmatrix} &\stackrel{\scriptscriptstyle{0{,}1}}{\approx} \begin{bmatrix} 1035{,}5\\1035{,}5 \end{bmatrix} \mathrm{N} \\ \begin{bmatrix} F_{2x} \\ F_{2y} \\ \end{bmatrix} &\stackrel{\scriptscriptstyle{0{,}1}}{\approx} \begin{bmatrix} 0{,}0\\2928{,}9 \end{bmatrix} \mathrm{N} \\ \begin{bmatrix} F_{3x} \\ F_{3y} \\ \end{bmatrix} &\stackrel{\scriptscriptstyle{0{,}1}}{\approx} \begin{bmatrix} -1035{,}5\\1035{,}5 \end{bmatrix} \end{align*}

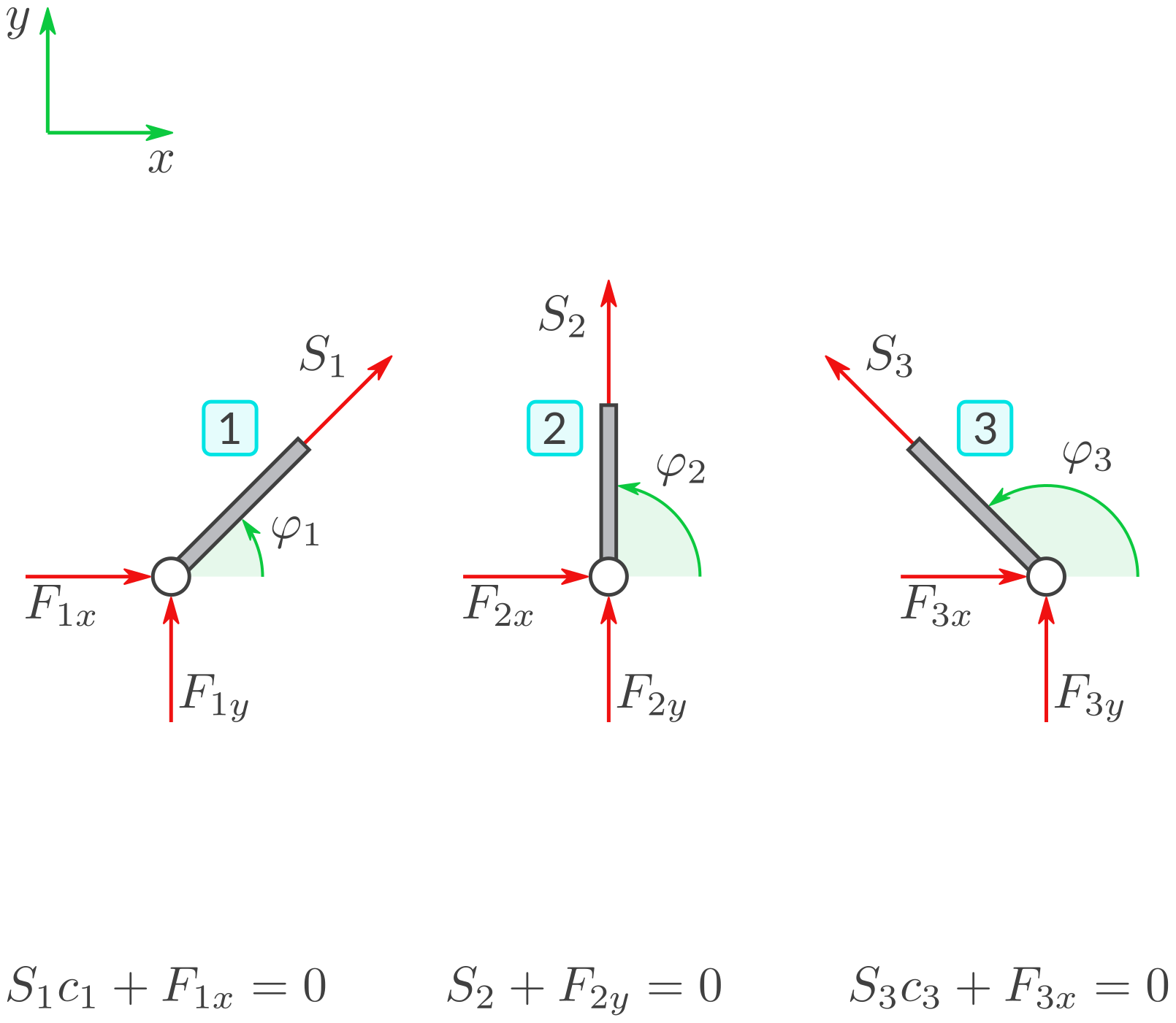
g) Stabkräfte

Berechnen Sie für dieselben Größen die Stabkräfte. Und zwar in \(\mathrm{N}\) (Newton) und gerundet auf Rundestellenwert \(0{,}1\):

\begin{align*} S_1 \stackrel{\scriptscriptstyle{0{,}1}}{\approx} \ldots \mathrm{N} \\ S_2 \stackrel{\scriptscriptstyle{0{,}1}}{\approx} \ldots \mathrm{N} \\ S_3 \stackrel{\scriptscriptstyle{0{,}1}}{\approx} \ldots \mathrm{N} \end{align*}

Lösung

../../../../_images/R2.A_1.png

Freischneiden und Auswertung der Gleichgewichtsbedingungen liefert Gleichungen, aus denen die Stabkräfte berechnet werden können. Einsetzen der gegebenen ‚Größen‘ liefert:

\begin{align*} S_1 \stackrel{\scriptscriptstyle{0{,}1}}{\approx} -1464{,}5 \, \mathrm{N} \\ S_2 \stackrel{\scriptscriptstyle{0{,}1}}{\approx} -2928{,}9 \, \mathrm{N} \\ S_3 \stackrel{\scriptscriptstyle{0{,}1}}{\approx} -1464{,}5 \, \mathrm{N} \end{align*}

Eine andere Methode zur Stabkraft-Berechnung siehe hier.

h) Symmetrie

Zeigen Sie, dass Sie bei Ausnutzung der Symmetrie dieselbe Lösung erhalten.

Lösung

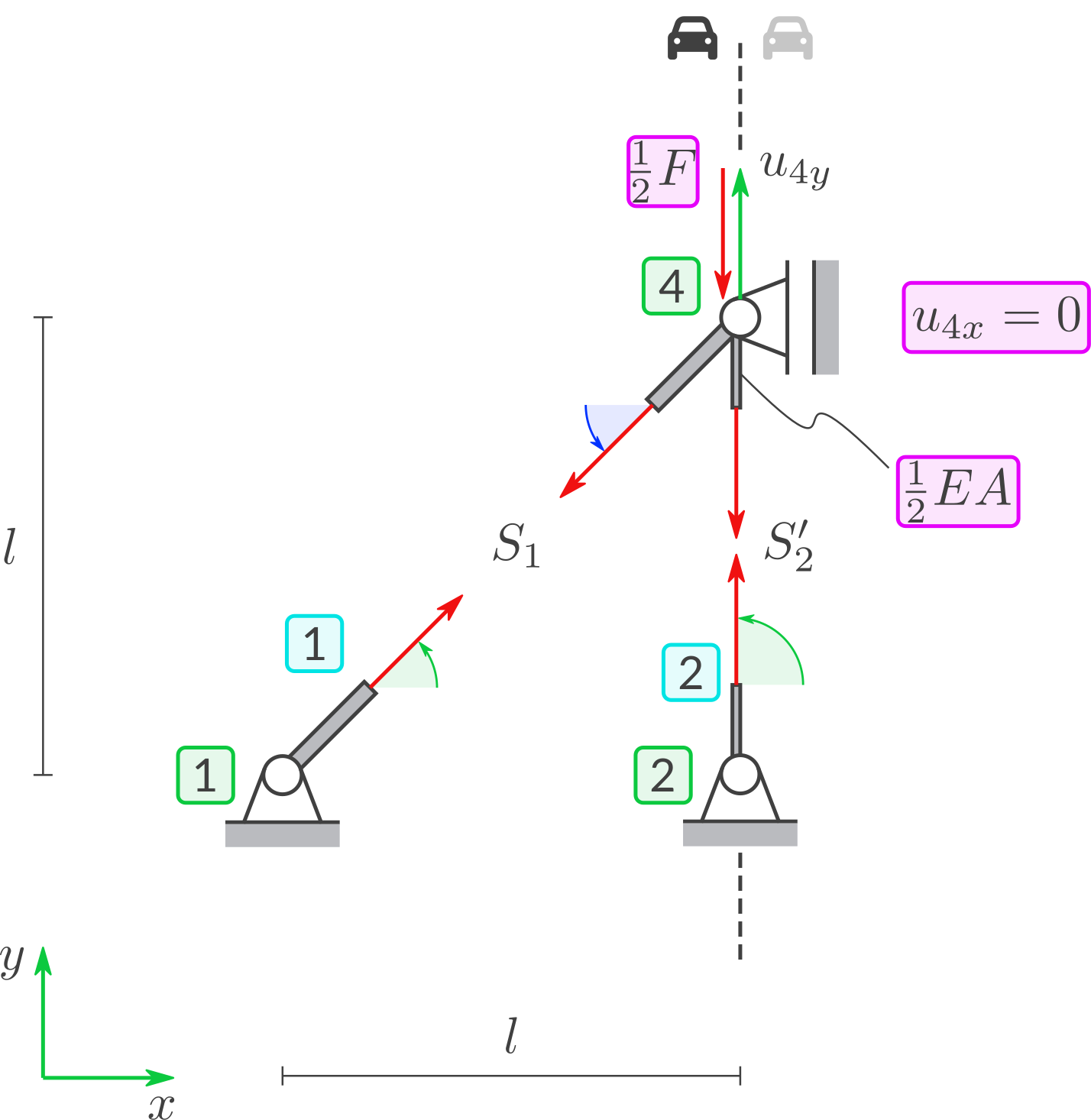
../../../../_images/R2.A_symm.png

Details

  • Achsensymmetrie und Betrachtung der linken Hälfte.

  • Kraft oben: \(\tfrac 12 F\).

  • Querschnitt Stab 2: \(\tfrac 12 EA\)

  • Zugkraft in Stab 2: \(S_2'\).

  • Loslager bei Knoten 4 erzwingt: \(u_{4x}=0\).

Steifigkeitsmatrizen:

\begin{align*} k^|_1 &= \tfrac{EA}{\sqrt 2 l} \left[ \begin{array}{cccc|c} \tfrac{1}{2} & \tfrac{1}{2} & - \tfrac{1}{2} & - \tfrac{1}{2} & u_{1x} \\ \tfrac{1}{2} & \tfrac{1}{2} & - \tfrac{1}{2} & - \tfrac{1}{2} & u_{1y} \\ - \tfrac{1}{2} & - \tfrac{1}{2} & \tfrac{1}{2} & \tfrac{1}{2} & u_{4x} \\ - \tfrac{1}{2} & - \tfrac{1}{2} & \tfrac{1}{2} & \tfrac{1}{2} & u_{4y} \\ \end{array} \right] \\ k^|_2 &= \tfrac12 \tfrac{EA}{l} \left[ \begin{array}{cccc|c} 0 & 0 & 0 & 0 & u_{2x} \\ 0 & 1 & 0 & -1 & u_{2y} \\ 0 & 0 & 0 & 0 & u_{4x} \\ 0 & -1 & 0 & 1 & u_{4y} \\ \end{array} \right] \\ K^|_1 &= \tfrac{EA}{\sqrt 2 l} \left[ \begin{array}{cccccc|c} \frac{1}{2} & \frac{1}{2} & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} & u_{1x} \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} & u_{1y} \\ 0 & 0 & 0 & 0 & 0 & 0 & u_{2x} \\ 0 & 0 & 0 & 0 & 0 & 0 & u_{2y} \\ - \frac{1}{2} & - \frac{1}{2} & 0 & 0 & \frac{1}{2} & \frac{1}{2} & u_{4x} \\ - \frac{1}{2} & - \frac{1}{2} & 0 & 0 & \frac{1}{2} & \frac{1}{2} & u_{4y} \\ \end{array} \right] \\ K^|_2 &= \tfrac{EA}{\sqrt 2 l} \left[ \begin{array}{cccccc|c} 0 & 0 & 0 & 0 & 0 & 0 & u_{1x} \\ 0 & 0 & 0 & 0 & 0 & 0 & u_{1y} \\ 0 & 0 & 0 & 0 & 0 & 0 & u_{2x} \\ 0 & 0 & 0 & \frac{\sqrt{2}}{2} & 0 & - \frac{\sqrt{2}}{2}& u_{2y} \\ 0 & 0 & 0 & 0 & 0 & 0 & u_{4x} \\ 0 & 0 & 0 & - \frac{\sqrt{2}}{2} & 0 & \frac{\sqrt{2}}{2}& u_{4y} \\ \end{array} \right] \\ K^| &= \tfrac{EA}{\sqrt 2 l} \left[ \begin{array}{cccccc|c} \frac{1}{2} & \frac{1}{2} & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} & u_{1x} \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} & u_{1y} \\ 0 & 0 & 0 & 0 & 0 & 0 & u_{2x} \\ 0 & 0 & 0 & \frac{\sqrt{2}}{2} & 0 & - \frac{\sqrt{2}}{2} & u_{2y} \\ - \frac{1}{2} & - \frac{1}{2} & 0 & 0 & \frac{1}{2} & \frac{1}{2} & u_{4x} \\ - \frac{1}{2} & - \frac{1}{2} & 0 & - \frac{\sqrt{2}}{2} & \frac{1}{2} & \frac{1}{2} + \frac{\sqrt{2}}{2} & u_{4y} \\ \end{array} \right] \end{align*}

Lineares System:

\begin{align*} \tfrac{EA}{\sqrt 2 l} \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & - \frac{1}{2} & - \frac{1}{2} \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{\sqrt{2}}{2} & 0 & - \frac{\sqrt{2}}{2} \\ - \frac{1}{2} & - \frac{1}{2} & 0 & 0 & \frac{1}{2} & \frac{1}{2} \\ - \frac{1}{2} & - \frac{1}{2} & 0 & - \frac{\sqrt{2}}{2} & \frac{1}{2} & \frac{1}{2} + \frac{\sqrt{2}}{2} \\ \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ u_{4y} \\ \end{bmatrix} &= \begin{bmatrix} F_{1x} \\ F_{1y} \\ F_{2x}' \\ F_{2y}' \\ F_{4x} \\ -\frac 1 2 F \\ \end{bmatrix} \end{align*}

Ergebnisse:

\begin{align*} u_{4y} &= \left(-2 + \sqrt 2\right) \tfrac{Fl}{EA} \\ \\ \begin{bmatrix} F_{2x}' \\ F_{2y}' \\ \end{bmatrix} &=\tfrac 1 2 \begin{bmatrix} 0 \\ - \sqrt 2 + 2 \\ \end{bmatrix} F \\ &=\tfrac 1 2 \begin{bmatrix} F_{2x} \\ F_{2y} \\ \end{bmatrix} \end{align*}

Dies ist dieselbe Lösung wie vorher. Weil Stab 2 halbiert wurde, sind die Lagerreaktionen bei Knoten 2 nur halb so groß wie beim Modell ohne Ausnutzung der Symmetrie.

SymPy

Python Source Code eines Programms dazu:

from sympy.physics.units import kg, m, s
from sympy import pi, S, pprint, symbols, sqrt, \
    cos, sin, Matrix, zeros, simplify, Eq, solve

# Units:
N         =  kg*m/s**2
k, M, G   =  10**3, 10**6, 10**9
kN        =  k*N
Pa        =  N/m**2
MPa, GPa  =  M*Pa, G*Pa
deg       =  pi/180
half      =  S(1)/2
mm        =  m/1000

# Rounding:
def iso_round(x, pv):
    try:
        x = float(x)
        tmp = round(x, pv)
    except TypeError:
        from functools import partial
        func = partial(round, ndigits = pv)
        tmp = x.applyfunc(func)
    return tmp

def printout(x, unit=1, prec=None, sub_list=[]):
    x = x.subs(sub_list)
    x /= unit

    try: 
        x = x.applyfunc(simplify)
    except:
        x = x.simplify()
    if prec:
        x = iso_round(x, prec)
    pprint(x)
    return

# Header ends here.

def k(phi):
    """ computes entries inside stiffness matrix """
    # Input: phi:
    # - measured at first element node
    # - counted positively about z-axis
    # - starts at x-axis
    # - ends at rod axis between first
    #   and second element node
    (c, s) = ( cos(phi), sin(phi) )
    (cc, ss, sc) = ( c*c, s*s, s*c)
    return Matrix(
        [
        [ cc,  sc, -cc, -sc],
        [ sc,  ss, -sc, -ss],
        [-cc, -sc,  cc,  sc],
        [-sc, -ss,  sc,  ss],
        ])

def assemble(n,k,i,j):
    """ Add Element Stiffness Matrix
        into System Stiffness Matrix"""

    # n: Number of Nodes
    # k: Element Stiffness Matrix
    # (i, j): Node Number of (First, Second) Element Node
    assert i in range(1,10)
    assert j in range(1,10)

    K = zeros(2*n,2*n)
    
    # swap if necessary:
    if (i < j):
        I, J = (i-1)*2, (j-1)*2
    else:
        I, J = (j-1)*2, (i-1)*2
    K[I:I+2, I:I+2]+=k[0:2,0:2]
    K[I:I+2, J:J+2]+=k[0:2,2:4]
    K[J:J+2, I:I+2]+=k[2:4,0:2]
    K[J:J+2, J:J+2]+=k[2:4,2:4]
    return K

F, l, E, A = symbols("F, l, E, A")
EA = E*A
r = sqrt(2)
sub_list = [
    ( F,     5 *kN    ),
    ( E,   200 *GPa   ),
    ( A,    25 *mm**2 ),
    ( l,  1707 *mm    ),
    ]

# Element stiffness matrices:
p1, p2, p3 = 45 *deg, 90 *deg, 135 *deg
l1, l2, l3 = r*l, l, r*l

k1 = EA/l1 * k(p1)
# k2 see below
k3 = EA/l3 * k(p3)

symm = True
symm = False

if not symm:
    print("\nNot Using Symmetry:")
    k2 = EA/l2 * k(p2)
    K1 = assemble(4, k1,4,1)
    K2 = assemble(4, k2,4,2)
    K3 = assemble(4, k3,4,3)

    pprint("\nK1 / (EA / √2 l):")
    pprint( K1 / (EA/(r*l)) )
    pprint("\nK2 / (EA / √2 l):")
    pprint( K2 / (EA/(r*l)) )
    pprint("\nK3 / (EA / √2 l):")
    pprint( K3 / (EA/(r*l)) )

    # System stiffness matrix:
    pprint("\nK / (EA / √2 l):")
    K = K1 + K2 + K3
    tmp = K
    tmp /= EA / (r*l)
    tmp = tmp.applyfunc(simplify)
    pprint(tmp)

    u1x,u1y,u2x,u2y,u3x,u3y,u4x,u4y=\
        symbols('u1x u1y u2x u2y u3x u3y u4x u4y')
    F1x,F1y,F2x,F2y,F3x,F3y,F4x,F4y=\
        symbols("F1x F1y F2x F2y F3x F3y F4x F4y")

    u = Matrix([ 0 , 0 , 0 , 0 , 0 , 0 ,u4x,u4y])
    f = Matrix([F1x,F1y,F2x,F2y,F3x,F3y, 0 ,-F ])

    unks = [u4x,u4y,F1x,F1y,F2x,F2y,F3x,F3y]

    eq = Eq(K*u, f)
    sol = solve(eq,unks)

    u4x,u4y,F1x,F1y,F2x,F2y,F3x,F3y = sol[u4x],sol[u4y],\
        sol[F1x],sol[F1y],sol[F2x],sol[F2y],sol[F3x],sol[F3y]

    pprint("\n(u4x, u4y) / (Fl / EA):")
    u4 = Matrix([u4x, u4y])
    printout(u4, F*l/EA, prec=None, sub_list=[])

    pprint("\nu4y / mm:")
    printout(u4y, unit=mm, prec=4, sub_list=sub_list)

    pprint("\n(F1x, F1y) / F:")
    rf = Matrix([F1x, F1y])
    printout(rf, F, prec=None, sub_list=[])

    pprint("\n(F1x, F1y) / N:")
    printout(rf, unit=N, prec=1, sub_list=sub_list)

    pprint("\n(F2x, F2y) / F:")
    rf = Matrix([F2x, F2y])
    printout(rf, F, prec=None, sub_list=[])

    pprint("\n(F2x, F2y) / N:")
    printout(rf, unit=N, prec=1, sub_list=sub_list)

    pprint("\n(F3x, F3y) / F:")
    rf = Matrix([F3x, F3y])
    printout(rf, F, prec=None, sub_list=[])

    pprint("\n(F3x, F3y) / N:")
    printout(rf, unit=N, prec=1, sub_list=sub_list)

    pprint("\n(S1, S2, S3) / N:")
    tmp = "("
    c1, c3 = cos(p1), cos(p3)
    S1, S2, S3 = - F1x / c1, - F2y, - F3x / c3
    for S in [S1, S2, S3]:
        printout(S, unit=N, prec=1, sub_list=sub_list)

elif symm:
    print("\nUsing Symmetry:")
    k2 = EA/2/l2 * k(p2)
    K1 = assemble(3,k1,3,1)
    K2 = assemble(3,k2,3,2)

    pprint("\nK1 / ( EA / (√2 l) ):")
    printout(K1, EA/(r*l), prec=None, sub_list=[])

    pprint("\nK2 / ( EA / (√2 l) ):")
    printout(K2, EA/(r*l), prec=None, sub_list=[])

    # System stiffness matrix:
    pprint("\nK / ( EA / (√2 l) ):")
    K = K1 + K2
    printout(K, EA/(r*l), prec=None, sub_list=[])

    u1x,u1y, u2x, u2y,u4x,u4y = symbols('u1x u1y  u2x  u2y u4x u4y')
    F1x,F1y,F2px,F2py,F4x,F4y = symbols("F1x F1y F2px F2py F4x F4y")

    u = Matrix([ 0 , 0 ,  0  ,  0 ,  0  , u4y])
    f = Matrix([F1x,F1y, F2px,F2py, F4x ,-F/2])

    unks = [u4y,F1x,F1y,F2px,F2py,F4x]
    eq = Eq(K*u, f)
    sol = solve(eq,unks)
    u4y,F1x,F1y,F2px,F2py,F4x = \
        sol[u4y],sol[F1x],sol[F1y],sol[F2px],sol[F2py],sol[F4x]

    pprint("\nu4y / ( Fl / (EA) ):")
    printout(u4y, F*l/EA, prec=None, sub_list=[])

    pprint("\n(F2'x, F2'y) / F:")
    printout(Matrix([F2px, F2py]), F, prec=None, sub_list=[])

Programm ausführen? Dazu:

  1. Copy: Source Code in die Zwischenablage kopieren.

  2. Paste: Source Code ins Eingabefeld hinter [ ]: einfügen.

  3. Play: Knopf ▶ drücken.