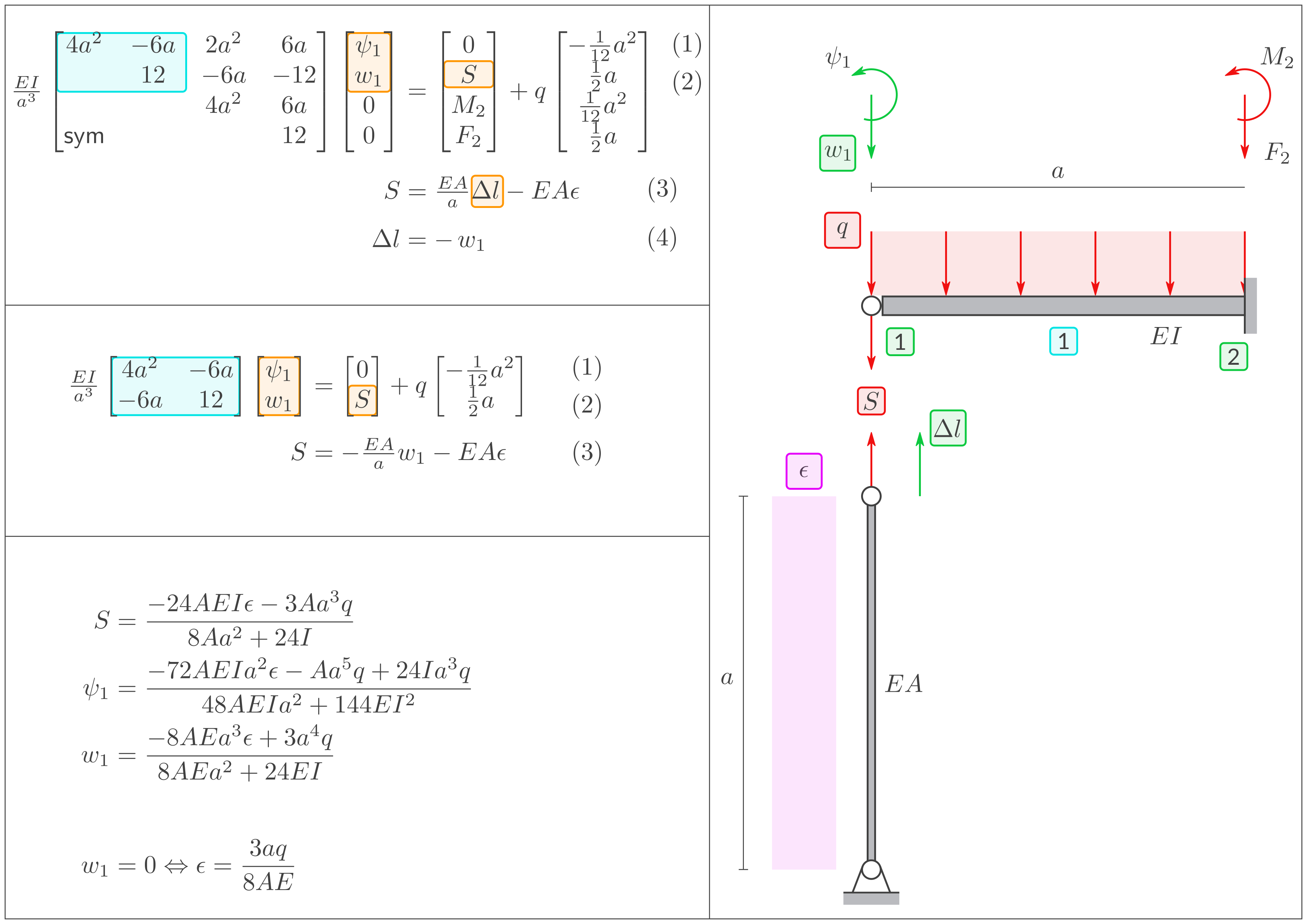
R2B2.B

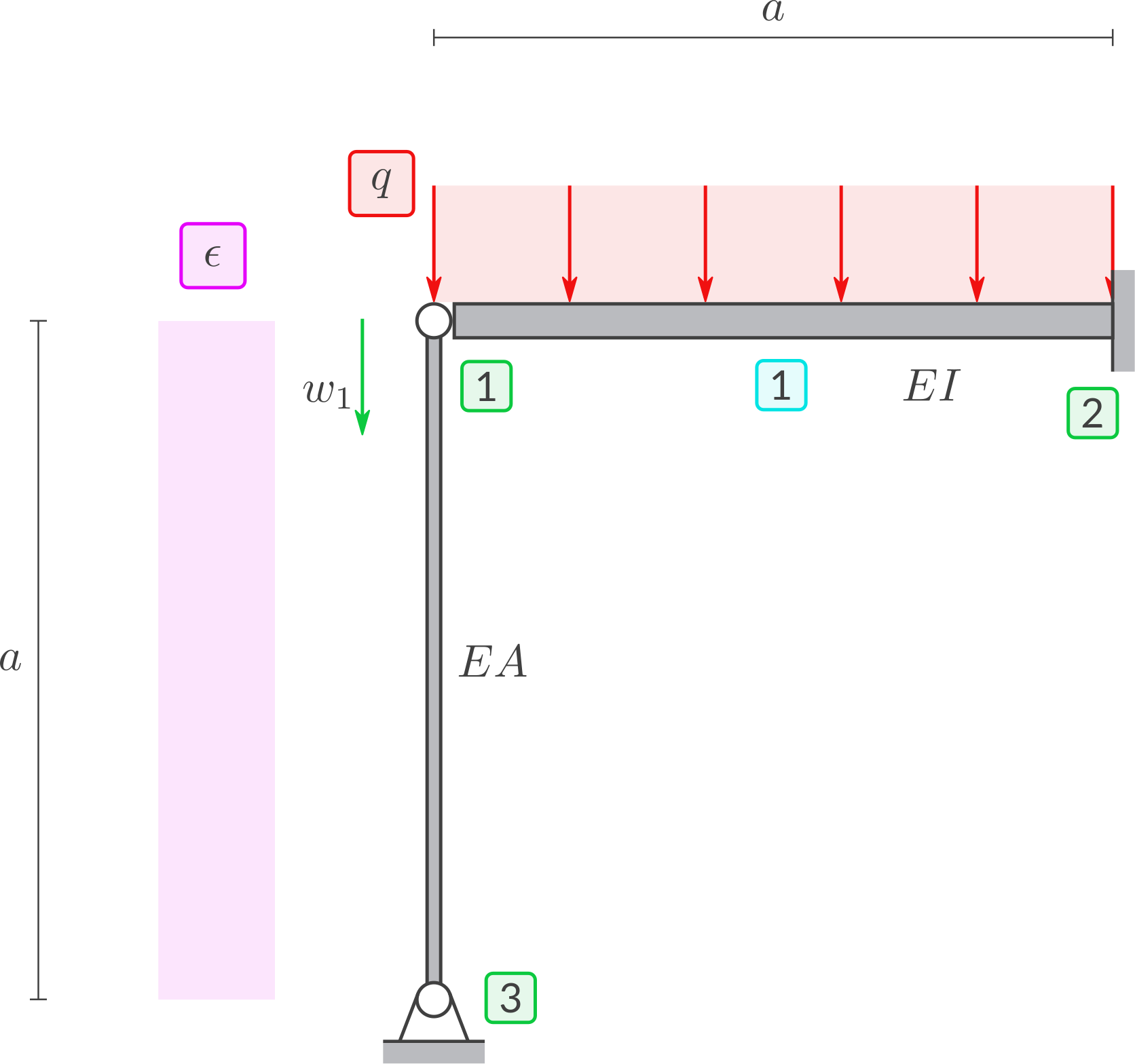
Gegebene Symbole: \(a, q, EA, EI\) und die Wärmeausdehnung (Verzerrung aufgrund Temperaturzuwachs) \(\epsilon\).

Berechnen Sie:

• die Verschiebung \(w_1\) von Knoten 1

• die Wärmedehnung \(\epsilon\), sodass \(w_1=0\).

Lösung "Freischneiden"

Ein Balken-Element B2 sowie ein Stab mit Elastizität \(S = \tfrac{EA}{a} \Delta l - EA \epsilon\). Beide Strukturen zusammengeführt über gemeinsame Kraft \(S\) und gemeinsame Verschiebung \(\Delta l = -w_1\).

Lösung "Gemeinsame Freiheitsgrade"

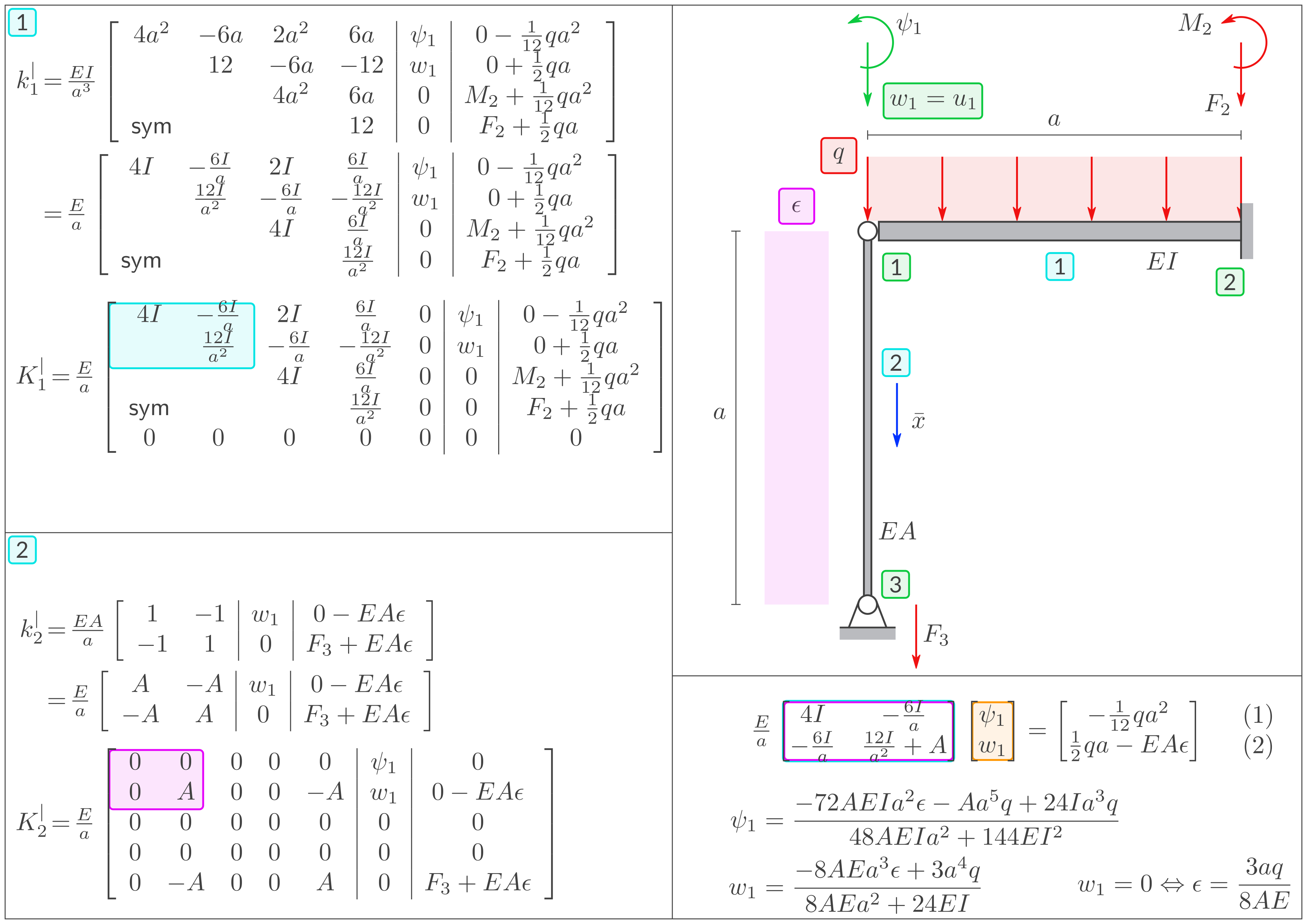
Ein 1D Stab-Element R2 und ein Balken-Element B2. Gemeinsamer Freiheitsgrad: \(w_1 = u_1\).

SymPy

Source Code eines Programms dazu:

from sympy.physics.units import *
from sympy import *

deg       =  pi/180

# ---

a, q, A, I, E, eT = var("a, q, A, I, E, ϵ")
EA, EI = E*A, E*I
a2 = a*a
a3 = a*a*a

pprint("Using \"FBD\":")
S, psi1, w1 = var("S, psi1, w1")
eq1 = Eq(S, - EA/a * w1 - EA * eT  )

K11 = 4*a2
K12 = -6*a
K21 = K12
K22 = 12

K = Matrix([
    [K11, K12 ],
    [K21, K22 ],
    ])
K *= EI/a3

u = Matrix([psi1, w1])
f = Matrix([0, S]) + q*Matrix([-a2/12, a/2])

eq2 = Eq(K*u, f)

eqns = [eq1, eq2]
unks = [S, psi1, w1]
sol = solve(eqns,unks)

psi1, w1 = sol[psi1], sol[w1]
pprint("\nψ₁:")
pprint(psi1)
pprint("\nw₁:")
pprint(w1)


pprint("\neT:")
sol = solve( Eq(w1,0), eT)
tmp = sol[0]
pprint(tmp)

pprint("\nUsing \"Shared Dofs\":")
psi1, w1 = var("psi1, w1")

K11 = 4*I
K12 = -6*I/a
K21 = K12
K22 = 12*I/a2 + A

K = Matrix([
    [K11, K12 ],
    [K21, K22 ],
    ])
K *= E/a

u = Matrix([psi1, w1])
f = Matrix([0, -EA*eT]) + q*Matrix([-a2/12, a/2])


eq = Eq(K*u, f)
unks = [psi1, w1]
sol = solve(eq,unks)

psi1, w1 = sol[psi1], sol[w1]
pprint("\nψ₁:")
pprint(psi1)
pprint("\nw₁:")
pprint(w1)

Programm im nachfolgenden Frame ausführen? Dazu:

1. Copy: Source Code in die Zwischenablage kopieren.

2. Paste: Source Code ins Eingabefeld hinter [ ]: einfügen.

3. Play: Knopf ▶ drücken.